Список объектов Солнечной системы по размеру

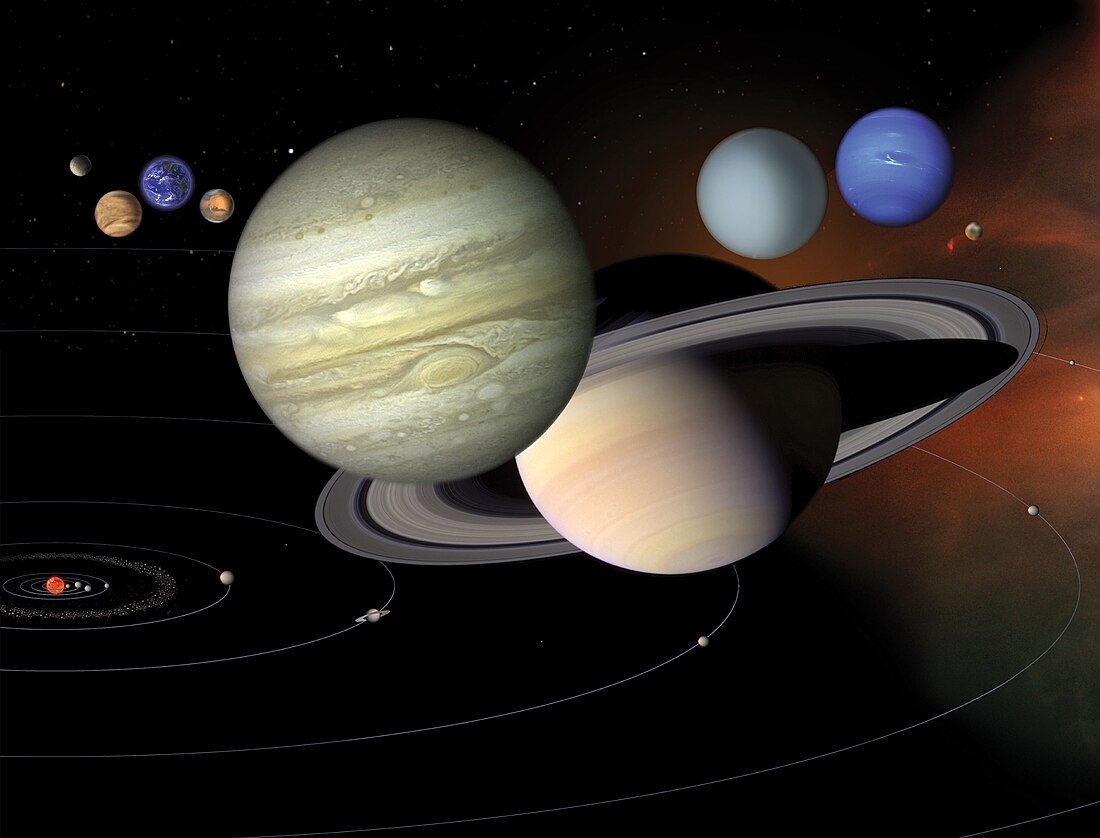
В данном списке объекты Солнечной системы представлены в порядке убывания среднего радиуса. В него входят Солнце, восемь основных планет и их спутники, карликовые планеты и кандидаты в карликовые планеты, а также наиболее крупные астероиды и ряд других объектов, представляющих исторический или научный интерес, таких как кометы и околоземные астероиды.

Сравнительные размеры планет и Солнца

Порядок расположения объектов в списке может быть разным в зависимости от того, по какому из параметров (размеру или массе) проводить упорядочение, поскольку разные объекты обладают разной плотностью. Например, Уран превышает по размеру Нептун, но несмотря на это уступает ему по массе, точно так же Ганимед и Титан больше Меркурия, а между тем вдвое уступают ему по массе. Это означает, что некоторые объекты внизу таблицы, несмотря на меньший размер, на деле могут оказаться массивнее тех, что находятся вверху, поскольку имеют бо́льшую плотность.

Сравнение масс самых тяжёлых объектов Солнечной системы

В последнее время открыто немало транснептуновых объектов, но из-за большого расстояния до них точно определить размеры объектов довольно затруднительно, поэтому их расположение в данном списке зачастую очень приблизительно.

Во всех объектах Солнечной системы массой более 10²¹ кг сила гравитации становится настолько значительной, что начинает преодолевать структурную прочность пород, придавая телу сфероидальную форму. Именно такая форма объекта позволяет скомпенсировать силу тяжести по всем направлениям и достичь гидростатического равновесия. При этом лёд обладает большей пластичностью, чем камень, поэтому для ледяных астероидов пояса Койпера значение массы, необходимой для придания телу сфероидальной формы, может быть гораздо меньше. При этом граница минимальных радиусов сфероидальных тел в обоих случаях совпадает и составляет примерно 200 км^[1].

Пример тела с массой около 10¹⁸ кг, не способного полностью принять сферическую форму (спутник Сатурна Янус)

Процессы изменения формы под действием сил тяжести начинают происходить в телах с массами от 10¹⁸ до 10²¹ кг, но форму равновесного сфероида принимают лишь крупные тела ближе к верхней границе массы, такие как Церера, Тефия, Мимас. Форма более мелких объектов, масса которых близка к 10¹⁸ кг, таких как Амальтея или Янус, менее правильна.

Кроме того, сферические тела имеют несколько сплющенную у полюсов форму, что вызвано ускорением под действием центробежной силы от вращения тела, в то время как у объектов, принявших сферическую форму лишь частично, существует значительная разница между любыми двумя экваториальными диаметрами.

Большие трудности в определении размеров имеют место для объектов, находящихся за пределами орбиты Сатурна — в таких случаях плотность тела условно принимают равной 2,000 г/см³, что примерно соответствует плотности смеси водяного льда с космической пылью, из которых, как правило, и состоит большинство объектов на таком расстоянии от Солнца, хотя велика вероятность, что на большом удалении от Солнца плотность астероидов сравнима с плотностью комет и составляет всего 0,5 г/см³^[2]. Значительно проще обстоит дело с двойными системами — в таких случаях по взаимному вращению компонентов оценить массу обоих тел достаточно легко. Таким образом, измерения размера и массы большинства транснептуновых объектов носит оценочный характер и может отличаться на порядок от реальных значений. Например, для одного из ТНО значение размера и плотности были оценены как 350 км и плотность 2,000 г/см³ соответственно, что указывало на массу объекта в 3,59⋅10²⁰ кг, в то время как реальный размер объекта составлял лишь 175 км, а плотность 1,000 г/см³, что говорило о массе уже в 2,24⋅10¹⁹ кг.

Размеры и массы большинства крупных спутников Юпитера и Сатурна известны достаточно хорошо в связи с пролётами таких исследовательских аппаратов, как «Галилео» и «Кассини», но размеры малых спутников этих планет-гигантов, таких как Гималия, по-прежнему зачастую носят лишь оценочный характер^[3]. Кроме того, по мере удаления от Солнца подробность и достоверность данных значительно снижается, и даже для крупных спутников Урана и Нептуна, несмотря на пролёт «Вояджера-2», данные весьма приблизительны и часто противоречивы^[3][4].

• 
  Сравнительная диаграмма масс тел Солнечной системы. В данном масштабе объекты с массой меньше массы Сатурна не видны.
• 
  Сравнительная диаграмма масс планет Солнечной системы. Масса Юпитера составляет 71 %, а масса Сатурна 21 % от суммарной массы всех планет. Масса планет земной группы весьма незначительна, у Меркурия она составляет всего 0,1 %, что в данном масштабе не видно.
• 
  Сравнительная диаграмма масс твёрдых тел Солнечной системы. Масса Земли составляет 48 %, Венеры — 39 %. Тела массой меньше массы Плутона здесь не видны.

Объекты диаметром от 400 км

Размеры этих тел лежат, как правило, значительно выше границы гидростатического равновесия, большинство объектов имеют почти чёткую сферическую форму. В таблице приведены параметры объектов не только в абсолютных значениях физических величин (км, км³, кг, м/с²), но и в относительных — в земных диаметрах (D_♁), объёмах (V_♁), массах (M_♁), ускорениях свободного падения (g_♁).

Объект	Фото	Средний диаметр		Объём		Масса		Плот­ность[5], г/см³	Уск. св. пад.		Тип объекта
		км	D♁	109 км³	V♁	1021 кг	M♁		м/с²	g♁
Солнце		1 392 000	109,245	1 412 000 000	1 303 781	1 989 100 000	332 837	1,409	274,0	28,02	Звезда
Юпитер		139 822	10,973	1 431 280	1 321	1 898 600	317,83	1,33	24,79	2,535	Планета
Сатурн		116 464	9,14	827 130	764	568 460	95,159	0,70	10,445	1,06	Планета
Уран		50 724	3,981	68 340	63,1	86 832	14,536	1,30	8,87	0,90	Планета
Нептун		49 244	3,865	62 540	57,7	102 430	17,147	1,638	11,15	1,140	Планета
Земля		12 742	1	1083,21	1	5973,6	1	5,515	9,80665	1	Планета
Венера		12 103,6	0,950	928,43	0,857	4868,5	0,815	5,24	8,872	0,91	Планета
Марс		6780,0	0,532	163,18	0,151	641,85	0,107	3,94	3,728	0,38	Планета
Ганимед† Юпитер III		5262,4	0,413	76,30	0,0704	148,2	0,0248	1,936	1,428	0,15	Спутник Юпитера
Титан † Сатурн VI		5151±4[6]	0,404	71,52	0,0660	134,5	0,0225	1,88	1,354	0,14	Спутник Сатурна
Меркурий		4879,4	0,383	60,83	0,0562	330,2	0,0553	5,43	3,7	0,38	Планета
Каллисто† Юпитер IV		4820,6	0,378	58,65	0,0541	107,6	0,018	1,83	1,23603	0,126	Спутник Юпитера
Ио† Юпитер I		3643,0	0,286	25,32	0,0234	89,3	0,015	3,528	1,797	0,183	Спутник Юпитера
Луна		3474,2	0,2727	21,958	0,0203	73,5	0,0123	3,3464	1,625	0,166	Спутник Земли
Европа† Юпитер II		3122,0	0,245	15,93	0,0147	48	0,00803	3,01	1,314	0,134	Спутник Юпитера
Тритон† Нептун I		2706,8	0,212	10,38	0,0096	21,5	0,00359	2,061	0,779	0,0797	Спутник Нептуна
Плутон 134340		2376,6	0,181	7,15	0,0066	13,105	0,0022	2,0	0,658	0,062	Карликовая планета Объект пояса Койпера
Эрида R 136199		2340[7]	0,184	7	0,007	16,7[8]	0,0027	2,25	0,827	0,0677	Карликовая планета Рассеянный диск
Титания‡ Уран III		1577,8	0,124	2,06	0,0019	3,526	0,00059	1,72	0,378	0,0385	Спутник Урана
Рея‡ Сатурн V		1528,8	0,12	1,87	0,0017	2,3166	0,00039	1,23	0,265	0,027	Спутник Сатурна
Оберон† Уран IV		1522,8	0,119	1,85	0,0017	3,014	0,0005	1,63	0,347	0,035	Спутник Урана
Япет† Сатурн VIII		1471,2[9]	0,115	1,55	0,0014	1,9739	0,00033	1,08	0,223	0,0227	Спутник Сатурна
Макемаке RA 136472		1420[10]	0,111	1,8	0,002	3	0,00067	2,0	0,4	0,04	Карликовая планета Объект пояса Койпера
Хаумеа R 136108 2003 EL61		1300[11]	0,102	1,3-1,6	0,001	4,006	0,00069	2,551[12]	0,44	0,045	Карликовая планета Объект пояса Койпера
Харон† Плутон I		1212	0,0947	0,87	0,0008	1,52	0,00025	1,65	0,279	0,028	Спутник Плутона
Гун-гун*		1535	0,12	1,88	0,0017	1,81P	0,0003	2,0	0,168	0,017	Рассеянный диск
Умбриэль† Уран II		1169,4	0,0918	0,84	0,0008	1,2	0,00020	1,4	0,234	0,024	Спутник Урана
Ариэль ‡ Уран I		1157,8	0,091	0,81	0,0008	1,35	0,00022	1,67	0,269	0,027	Спутник Урана
Диона† Сатурн IV		1123,2	0,088	0,73	0,0007	1,096	0,000183	1,48	0,232	0,0236	Спутник Сатурна
Тефия‡ Сатурн III		1062,2	0,0837	0,624	0,0006	0,6173	0,000103	1,15	0,145	0,015	Спутник Сатурна
(90377) Седна*AR 90377		995	0,117	1,73	0,0016	3	0,00050	2,0	0,33 — 0,50	0,0337 — 0,0511	Обособленный ТНО
Церера‡		950	0,0746	0,437	0,0004	0,95	0,000159	2,08	0,27	0,0275	Карликовая планета Астероид
(202421) 2005 UQ5139		924	0,0722	0,443	0,0004	0,886P	0,0001	2,0	0,278	0,0284	Объект пояса Койпера Кьюбивано
Квавар *		890±70[13]	0,0698	0,37	0,0003	1,6[13]	0,0003	4,2[13]	0,125	0,013	Объект пояса Койпера, кьюбивано
(120347) Салация		870[14]	0,0467	0,102	0,00009	0,2P	0,000034	2,0P	0,159	0,016	Кьюбивано?
(90482) ОркRA		850[10]	0,0667	0,4	0,0004	0,63A	0,0001	1,5	0,234	0,023	Объект пояса Койпера Плутино
(174567) Варда		818	0,0658	0,308	0,0003	0,616P	0,0001	2,0	0,228	0,02	Объект пояса Койпера
2006 QH1819		764	0,06	0,233	0,000215	0,467P	0,00008	2,0	0,214	0,022	Рассеянный диск
(19521) Хаос*		600[14]	0,0585	0,216	0,0002	0,4328P	0,00007	2,0P	0,209	0,021	Объект пояса Койпера Кьюбивано
(278361) 2007 JJ43		730	0,0791	0,536	4,95⋅10-4	1,072P	0,000179	2,0	0,282	0,029	Транснептуновый объект[14]
(208996) 2003 AZ84		727	0,0714	0,169	0,000156	0,53P	5,66⋅10-5	2,0	0,172	0,02	Объект пояса Койпера Плутино
(84922) 2003 VS2 R		726[15]	0,057	0,203	0,00018	0,4005P	0,000067	2,0	0,204	0,02086	Плутино[14]
(307261) 2002 MS4 R		797[14]	0,0562	0,203	0,00018	0,4005P	0,000067	2,0P	0,204	0,02086	Объект пояса Койпера[14]
(55565) 2002 AW197R		700[16]	0,0549	0,207	0,00019	0,414P	0,000069	2,0	0,206	0,0211	Объект пояса Койпера[14]
(230965) 2004 XA192		339[14]	0,0549	0,177	0,00016	0,354P	0,000059	2,0	0,195	0,02	Транснептуновый объект[14]
2010 KZ39		697[14]	0,0549	0,177	1,63⋅10-4	0,354P	0,000059	2,0	0,195	0,02	Кьюбивано?[14]
(55637) 2002 UX25R		681±115[15]	0,0535	0,166	0,000153	0,331P	0,0000554	2,0	0,191	0,01952	Объект пояса Койпера
(145452) 2005 RN439		679	0,0573	0,2036	0,00019	0,407P	0,000068	2,0	0,205	0,02096	Транснептуновый объект[14]
(90568) 2004 GV9R		677[15]	0,0531	0,162	0,00015	0,325P	0,0000534	2,0	0,19	0,0194	Объект пояса Койпера
(28978) ИксионRA		650[15]	0,051	0,144	0,000133	0,3	5,0⋅10-5	2,086	0,19	0,021	Объект пояса Койпера
(42301) 2001 UR1639		554[14]	0,0499	0,134	0,00012	0,269P	0,000045	2,0	0,178	0,018	Резонанс 4:9[14]
(20000) Варуна*		620[15]	0,049	0,125	0,000115	0,37	6 2⋅10-5	0,992[12]	0,258	0,028	Объект пояса Койпера
2003 UZ4139		606,6	0,048	0,116	0,00012	0,33P	0,000055	2,0	0,241	0,0246	Объект пояса Койпера
(229762) 2007 UK1269		599	0,0689	0,354	0,0003	0,708P	0,0001	2,0	0,246	0,025	Рассеянный диск
(84522) 2002 TC302R		584,1[17]	0,089	0,786	0,0007	1,573P	0,00026	2,0	0,321	0,033	Объект пояса Койпера 2:5
(145451) 2005 RM439		580[14]	0,0455	0,102	0,00009	0,2P	0,000034	2,0	0,159	0,016	Объект пояса Койпера
2004 NT33		423[14]	0,0455	0,089	0,000082	0,178P	0,000029	2,0	0,155	0,0158	Объект пояса Койпера Кьюбивано?[14]
(15874) 1996 TL66RA		576	0,045	0,1	9,2⋅10-5	0,2	3,3⋅10-5	1,999	0,162	0,018	Рассеянный диск
2004 XR190*		607[14]	0,059	0,221	0,0002	0,4416P	0,00007	2,0P	0,21	0,0215	Рассеянный диск[14]
(120348) 2004 TY364*		365[14]	0,043	0,089	0,000082	0,178P	0,000029	2,0	0,155	0,0158	Объект пояса Койпера[14]
(38628) ГуйяR		532[15]	0,04175	0,0788	0,000073	0,158P	0,00026	2,0	0,15	0,015	Объект пояса Койпера Плутино
(2) Паллада$		545[18]	0,04175	0,078	0,00007	0,211	0,0000353	2,8[19]	0,2	0,02	Астероид
(4) Веста$		529,2	0,04175	0,078	0,00007	0,262	0,0000438	3,42[20]	0,251	0,0256	Астероид
2003 QX113		505[14]	0,0396	0,051	0,00005	0,102P	0,000017	2,0P	0,129	0,013	Транснептуновый объект[14]
Энцелад‡ Сатурн II		504,2	0,0396	0,067	0,00006	0,108	0,0000181	1,61	0,111	0,0113	Спутник Сатурна
Миранда‡ Уран V		471,4	0,037	0,055	0,00005	0,0659	0,000011	1,20	0,0791	0,00806	Спутник Урана
(26375) 1999 DE9		461[15]	0,036	0,051	0,000047	0,1026P	0,000017	2,0	0,129	0,013	Объект пояса Койпера
2002 XV93		549[14]	0,0344	0,051	0,00005	0,102P	0,000017	2,0	0,129	0,013	Плутино[14]
(120132) 2003 FY128*		460[14]	0,0344	0,0446	0,00004	0,089P	0,000014	2,0	0,123	0,0126	Транснептуновый объект[14]
(35671) 1998 SN165*		433[14]	0,036	0,05	0,000046	0,1P	0,000017	2,0	0,128	0,013	Объект пояса Койпера
(82075) 2000 YW134*		229[14]	0,0335	0,065	0,00006	0,13P	0,000022	2,0P	0,139	0,014	Резонанс 3:8[14]
1999 CD158		420[14]	0,033	0,0446	0,00004	0,089P	0,000014	2,0	0,123	0,0126	Кьюбивано?
Протей ‡A Нептун VIII		420	0,033	0,038	0,000035	0,050	0,00000844	1,3[21]	0,0666	0,00678	Спутник Нептуна
2001 QF298*		408[14]	0,033	0,067	0,00006	0,134P	0,000022	2,0	0,141	0,014	Плутино[14]
(303775) 2005 QU1829		416	0,0722	0,606	0,00056	1,21P	0,0002	2,0	0,294	0,03	Рассеянный диск[14]
(10) Гигея$		407,12[22][23]	0,032	0,04	0,00003	0,0885	1,0⋅10-5	2,5	0,143	0,02	Астероид
(119979) 2002 WC19		401[24]	0,0315	0,034	0,00003	0,0675P	0,000011	2,0	0,113	0,0115	Объект пояса Койпера
2018 AG37		400[25][26]									Транснептуновый объект

Объекты диаметром от 200 до 400 км

Самые крупные из этих объектов лежат выше гидростатического равновесия и имеют сферическую форму, но большинство приняли сферическую форму лишь частично, сохранив существенный перепад высот на поверхности. Для большинства транснептуновых объектов, перечисленных в этой таблице, размер предполагается из условия альбедо поверхности 0,09, поскольку они слишком далеки, чтобы непосредственно оценить их размеры. Данный список не является полным из-за отсутствия данных о многих ТНО^[14][27].

Объект	Фото	Средний диаметр, км	Масса, 1018 кг	Тип объекта
(445473) 2010 VZ98		450[28]	?	Объект рассеянного диска
(144897) 2004 UX10		398[14]	30	Объект пояса Койпера
Мимас‡ Сатурн I		396,6	37,49	Спутник Сатурна
(307616) 2003 QW90P		366[14]	58,8	Кьюбивано
2002 CY248P		383[14]	58,8	Кьюбивано
(15789) 1993 SCP		375[14]	50,9	Транснептуновый объект — плутино[14]
(145480) 2005 TB190P		372,5[29]	54,1	Обособленный ТНО
C/2014 UN271 (Бернардинелли — Бернштейна)		370—130[30]	?	Комета Облака Оорта[31]
(55636) 2002 TX300		360	12	Объект пояса Койпера — семейство Хаумеа
(48639) 1995 TL8*P		350	44,9	Объект пояса Койпера — двойной астероид
Нереида A Нептун II		340	31	Спутник Нептуна
(511) Давида$		326,06	43,8	Главный пояс — класс C
(47932) 2000 GN171P		321[15]	34,6	Транснептуновый объект — плутино
(79978) 1999 CC1589P		319[14]	29,4	Резонанс 5:12
(704) ИнтерамнияM		316,62[32]	37	Главный пояс — класс F
Хииака Хаумеа I		310	20	Спутник Хаумеа
1995 SN55*P		310	31,2	Кентавры
(40314) 1999 KR169		304	29,4	Транснептуновый объект
(52) Европа$		302,5	16,5	Главный пояс — класс C
(47171) 1999 TC36 (A1)P		286[33]	24,5	Объект пояса Койпера — тройной астероид (A1+A2+B)
(87) Сильвия$		285,6	14,78	Внешняя часть главного пояса — тройной астероид
(26308) 1998 SM165		279,8[15]	14	Объект пояса Койпера — двойной астероид
(65) Кибела$		273[34] 2004 118,7[35] IRAS	17,8	Внешняя часть главного пояса — класс C
Гиперион Сатурн VII		270[36]	5,58	Спутник Сатурна
(47171) 1999 TC36 (A2)P		265[33]	19,5	Объект пояса Койпера — тройной астероид (A1+A2+B)
(79360) Сила-НунамP		249[14]	29,7	Кьюбивано, двойной астероид
2005 PU219P		242[14]	19,5	Кентавр
(79983) 1999 DF99P		265	19,5	Транснептуновый объект — кьюбивано
(119878) 2002 CY224		265[14]	15	Резонанс 5:12
(26181) 1996 GQ21*		262[14]	67P	Рассеянный диск[14]
(107) Камилла$		258,8	11,2	Внешняя часть главного пояса — класс C — двойной астероид
(10199) ХариклоP		258,6[15]	18,1	Кентавры
(31) ЕвфросинаM		256	6,23	Главный пояс — класс C
(15) Эвномия$		255,4[37]	31,2	Главный пояс — класс S
(145453) 2005 RR43P		252[38][39]	16,7	Объект пояса Койпера — семейство Хаумеа
(148209) 2000 CR105*A		242[14]	13	Обособленный ТНО
(3) Юнона $		233,92[32]	26,7	Главный пояс — класс S
(2060) Хирон*A 95P/Chiron		233,4	10	Кентавры
(88) Фисба$M		232[40]	10,5	Главный пояс — класс B
(120178) 2003 OP32P		230	12,7	Объект пояса Койпера — семейство Хаумеа
2004 VN1129P		230	12,7	Рассеянный диск
2002 KW14P		230[41]	12,7	Объект пояса Койпера
(324) БамбергаM		228	10	Главный пояс — класс C
(451) ПациенцияP		225	15,4	Главный пояс
(19) Фортуна$		225[42]	12,7	Главный пояс — класс G
(532) ГеркулинаP		222	11,5	Главный пояс — класс S
(48) ДоридаA		221,8[43]	17	Главный пояс
(148780) Альчера 9		218[14]	31	Транснептуновый объект — кьюбивано
(375) Урсула		216[44]	10,5	Главный пояс
(45) ЕвгенияM		214	5,69	Главный пояс — класс F — тройной астероид
Феба $ Сатурн IX		213,2	8,29	Спутник Сатурна
(29) Амфитрита$		212	11,8	Главный пояс — класс S
(53311) ДевкалионP		211[14]	9,83	Транснептуновый объект — кьюбивано
(33001) 1997 CU29P		211	9,83	Транснептуновый объект — кьюбивано
(423) ДиотимаA		208,87[32]	16	Главный пояс — класс C
(181902) 1999 RD215P		146[14]	9,51	Рассеянный диск
(13) ЭгерияM		207,64[32]	16,3	Главный пояс — класс G
(54598) БиенорP		207±30[15]	9,3	Кентавры
(94) АврораP		205	9,0	Главный пояс
(624) ГекторA		203[45]	14	Астероид — троянец Юпитера (L4)— двойной астероид
(38083) РадамантP		201[14]	8,5	Плутино?
(19308) 1996 TO66P		200	8,4	Объект пояса Койпера — семейство Хаумеа

Объекты диаметром от 100 до 200 км

Размеры в этом диапазоне имеют большинство крупных астероидов и спутников газовых гигантов. Для астероидов, помимо радиуса и массы, указывается ещё и спектральный класс. Впрочем, представленный здесь список является неполным, в нём отсутствуют многие, недавно открытые, объекты транснептуновой области^[14].

Объект	Фото	Средний диаметр, км	Масса, 1018 кг	Тип объекта
(7) Ирида$		199,83[46]	13,6	Главный пояс — класс S
(24) ФемидаM		198,0	11,3	Главный пояс — класс C — семейство Фемиды
(702) Алауда		194,8[32]	6,05	Главный пояс — класс C — двойной астероид
ЛариссаA Нептун VII		194,0	4,2	Спутник Нептуна
(85633) 1998 KR65		201[14]		Объект пояса Койпера — кьюбивано
(121) ГермионаM		190,0	5,38	Внешняя часть главного пояса — класс C — двойной астероид
(372) Пальма		188,62[47]		Главный пояс
(128) Немезида		188,2	7	Главный пояс — класс C
(16) Психея$		186,0	21,9	Главный пояс — класс M
(6) Геба$		185,18[32]	12,8	Главный пояс — класс S
(5145) Фол		185,0[48]	6,6	Кентавры
(154) Берта		184,94[32]	5,2	Главный пояс — класс C
(76) Фрейя		183,66	6,5	Внешняя часть главного пояса — семейство Кибелы
(59358) 1999 CL1589		183,0		Транснептуновые объекты — неустойчивый
(130) ЭлектраM		182,2[32]	6,6	Астероид — класс G — двойной астероид
(119951) 2002 KX14		318[14]		Кьюбивано[14]
Янус$ Сатурн X		178,8	1,912	Спутник Сатурна
(259) Алетейя		178,6[32]	5,97	Главный пояс
Галатея Нептун VI		176,0[3]	2,12	Спутник Нептуна
Таронхайавагон		161[14]		Транснептуновые объекты — кьюбивано — двойной астероид
(42355) Тифон		175,0[15]		Транснептуновые объекты — двойной астероид
(19255) 1994 VK8		175[14]	5,6	Транснептуновые объекты — кьюбивано
(120) Лахесис		174,1[32]	5,5	Главный пояс
(65489) Кето		174,0[49]	5,4[49]	Кентавры — ТНО — двойной астероид
(24835) 1995 SM55		174,0		Объект пояса Койпера — семейство Хаумеа
(41) Дафна		174,0		Главный пояс
(9) Метида$		173,8	11,3	Главный пояс
(747) Винчестер		171,71[32]		Астероид
(153) Хильда		170,64[32]	5,2	Главный пояс — семейство Хильды
(790) Претория		170,4[50]		Внешняя часть главного пояса — семейство Кибелы
Гималия M Юпитер VI		170,0[3] — 92[51]	4,19[52]	Спутник Юпитера — Группа Гималии
Намака Хаумеа II		170,0	2	Спутник Хаумеа
(96) Эгла		169,9	5,1	Главный пояс
(241) Германия		168,9[32]	5,05	Главный пояс — класс C
(194) Прокна		168,42[32]	5	Главный пояс — класс C
(566) Стереоскопия[53]		168,16[32]		Внешняя часть главного пояса — семейство Кибелы
Амальтея Юпитер V		167[54]	2,08[55]	Спутник Юпитера$
(911) Агамемнон		166,6[32]		Астероид — троянец Юпитера (L4)
(22) Каллиопа		166,2[56]	8,09M	Главный пояс — класс M — двойной астероид
(66652) Борасизи		126[14]		Транснептуновые объекты — кьюбивано — двойной астероид
(54) Александра		165,75	5,0	Главный пояс
(386) Зигена		165,0[57]		Главный пояс — класс C
(59) Элпида		164,8		Главный пояс
(1437) Диомед		164,32[32]	4,6	Астероид — троянец Юпитера (L4)
(444) ГиптидаM		163,08[32]	12,5	Главный пояс — класс C
Пак Уран XV		162,0[3]	2,9A	Спутник Урана
(409) Аспасия		161,62[32]	4,42	Главный пояс — класс C
(20461) Диоретса		8[14]		Астероид — Дамоклоиды
1992 QB1		167[14]		Объект пояса Койпера — кьюбивано
(15875) 1996 TP66		160,0[15]		Объект пояса Койпера — внутренний плутино
(209) Дидона		159,94[32]	4,28	Главный пояс — класс C
(334) Чикаго		158,55[32]		Главный пояс — класс C
(804) Испания		157,58[32]	9,95	Главный пояс — класс P
(185) Эвника		157,51[32]	4,09	Главный пояс
(139) Жуйхуа		156,6[32]	4	Главный пояс
(354) Элеонора		155,17[32]		Главный пояс — класс S
(85) Ио		154,8[58]	3,4	Главный пояс
(165) Лорелей		154,78[32]	3,91	Главный пояс — класс C
(173) Ино		154,1[32]	3,83	Главный пояс — класс C
(11) Парфенопа		153,34[32]	6,15M	Главный пояс
(137295) 1999 RB216		146[14]		Объект пояса Койпера — тутино
(14) Ирена		152,0[59]	8,2	Главный пояс
(89) Юлия		151,5	3,6	Главный пояс — класс S
(536) Мерапи		151,4[32]		Главный пояс
(145474) 2005 SA278		253[14]		Рассеянный диск
(776) Бербериция		151,18[32]		Главный пояс
(145) Адеона		151,14[32]	3,6	Главный пояс — семейство Адеоны
(150) Нюйва		151,13[32]	3,62	Главный пояс — класс C
Дисномия		150[60][61]		Спутник Эриды
ДеспинаA Нептун V		150	2,1	Спутник Нептуна
Сикоракса		150[3]	2,3	Спутник Урана
(49) Палес M		149,8[32]	2,69	Главный пояс — класс C
(39) Летиция		149,52	3,5	Астероид
(117) Ломия		148,72[32]	3,4	Главный пояс — класс C
(238) Гипатия		148,49[32]	3,43	Главный пояс — класс C
(168) Сибилла		148,39[32]	3,42	Главный пояс — класс C
(283) ЭммаM		148,0	1,38	Астероид — двойной астероид
(51) Немауза		147,9	3,4	Астероид
(106) Диона		146,6	3,3	Главный пояс — класс G
(118378) 1999 HT11		133[14]		Резонанс 4:7
(137) Мелибея		145,42[32]	3,2	Главный пояс
(20) Массалия$		145,0	5,67	Астероид
(211) Изольда		143,2[32]	3,07	Главный пояс — класс C
(1172) Эней		142,82[62]		Астероид — троянец Юпитера (L5)
(144) Вибилия		142,38[32]	3	Главный пояс — семейство Вибилии
(508) Принстония		142,36[32][63]		Главный пояс
(895) Гелио		141,9[32]		Главный пояс — класс B
(361) Бонония		141,72[32]	2,98	Главный пояс — класс D
(420) Бертольда		141,05[32]		Главный пояс — класс P
(93) Минерва		141,0	2,9	Главный пояс — класс C — тройной астероид
(617) Патрокл		140,92[32]		Астероид — троянец Юпитера (L5) — двойной астероид
(308) Поликсо		140,69[32]	2,92	Главный пояс — класс T
(18) Мельпомена		140,6	3	Главный пояс
(268) Адорея		139,89[32]	2,87	Главный пояс
(349) Дембовска		139,77[32]	2,86	Главный пояс — класс R
(489) Комачина		139,39[32]		Главный пояс
(47171) 1999 TC36(B)		139,0[33]		Объект пояса Койпера — тройной астероид (A1+A2+B)
(69) Гесперия		138,14	2,76	Главный пояс — класс M
2003 UZ117		138,0		Объект пояса Койпера — семейство Хаумеа
(762) Пулкова		137,08[32]		Главный пояс — класс C — двойной астероид
(196) Филомела		136,39[32]	2,65	Главный пояс — класс S
(212) Медея		144±7[64]	13[64]	Главный пояс
(95) Аретуса		136,04[32]	2,6	Главный пояс
Порция Уран XII		135,2[3]	1,7	Спутник Урана
(712) Боливиана		127,57[32]		Главный пояс
(588) Ахиллес		135,47[32]		Астероид — троянец Юпитера (L4)
(690) Вратиславия		134,55[32]		Астероид
(111) Ата		134,56	2,6	Главный пояс — класс C
(247) Эвкрата		134,43[32]	2,54	Главный пояс — класс C
(705) Эрминия		134,22[32]		Главный пояс
(471) Папагена		134,19[32]		Главный пояс — класс C
Форкий Кето I		134	1,67[49]	Спутник астероида (65489) Кето
1998 WW31		133,0	2	Транснептуновые объекты — двойной астероид
(147) Протогенея		132,93[32]	2,5	Главный пояс
(344) Дезидерата		132,27[32]	2,42	Главный пояс — класс C
(146) Луцина		132,2[32]	2,4	Главный пояс
(141) Люмен		131,04[32]	1,6	Главный пояс — класс C
(356) Лигурия		131,31[32]		Главный пояс
(216) Клеопатра		131,0	4,64	Главный пояс — класс M — тройной астероид
(187) Ламберта		130,4[32]	2,37	Главный пояс — класс C
(419) Аврелия		129,01[32]		Главный пояс — класс F
(200) Динамена		128,36[32]		Главный пояс
(8) Флора		127,8	8,47	Главный пояс — класс S — семейство Флоры
(654) Зелинда		127,4[32]		Главный пояс
(426) Гиппо		127,1[32]		Главный пояс
(47) Аглая		126,96	2,1	Главный пояс — класс C
(279) Туле		126,59[32]	2,12	Главный пояс — класс D
(92) Ундина		126,42[65]	2,1	Главный пояс — класс M
(1173) Анхис(1930 UB)		126,27[32]		Астероид — троянец Юпитера (L5)
(1143) Одиссей		125,64[32]		Астероид — троянец Юпитера (L4)
(469) Аргентина		125,57[32]		Главный пояс — семейство Кибелы
(159) Эмилия		125,0	1,4	Астероид
(405) Тейя		124,9[32]		Главный пояс — класс C
(602) Марианна		124,72[32]		Главный пояс
(46) Гестия		124,14[32]	3,5[66]-21[67]	Главный пояс
(104) Климена		123,8	2	Главный пояс
(410) Хлорида		123,57[32]	1,97	Главный пояс — класс C — семейство Хлориды
(134) Софросина		123,28	2	Главный пояс
(328) Гудрун		122,92[32]	1,94	Главный пояс — класс S
(1867) Деифоб		122,67[32]		Астероид — троянец Юпитера (L5)
(68) Лето		122,6	1,9	Главный пояс — класс S
(70) Панопея		122,17	2,76	Главный пояс — класс C
(127) Жанна		122,0[68]		Главный пояс
(276) Аделаида		121,6[32]		Главный пояс
(176) Идуна		121,04[32]	1,76	Главный пояс — класс G
(156) Ксантиппа		120,99[32]	1,85	Главный пояс — класс S
(28) Беллона		120,9[32]		Главный пояс — класс C
(86) Семела		120,6		Главный пояс — класс C
(78) Диана		120,6		Главный пояс — класс C
(381) Мирра		120,58[32]		Главный пояс — класс C
(225) Генриетта		120,49[32]	1,83	Главный пояс — класс C — семейство Кибелы
(618) Эльфрида		120,29[32]		Главный пояс — класс C
(73840) 2002 PN34		119,5[15]		Рассеянный диск
(105) Артемида		119,2	1,8	Главный пояс — класс C
(81) Терпсихора		119,08	1,8	Главный пояс — класс C
(5) Астрея		119,07[32]	2,9	Главный пояс
(74) Галатея		118,72	1,8	Главный пояс — класс C
(350) Орнамента		118,35[32]		Главный пояс — класс C
(772) Танета		117,66[32]		Главный пояс — класс C
(476) Гедвиг		116,76[32]		Главный пояс
(1093) Фреда		116,73[32]		Главный пояс
(171) Офелия		116,7[32]	1,66	Главный пояс — класс C — семейство Фемиды
(909) Улла		116,44[32]		Астероид
(3317) Парис		116,26[32]		Астероид — троянец Юпитера (L5)
(203) Помпея		116,25[32]	1,65	Главный пояс
(3063) Махаон		116,14[32]	1,6	Астероид — троянец Юпитера (L4)
(38) Леда		115,93[32]	1,6	Астероид
(360) Карлова		115,76[32]		Главный пояс
(521) Бриксия		115,65[32]		Главный пояс
(490) Веритас		115,55[32]		Главный пояс — семейство Веритас
(466) Тисифона		115,53[32]		Главный пояс — класс C
(53) Калипсо		115,38		Астероид
(2241) Алкафой		114,63[32]		Астероид — троянец Юпитера (L5)
(388) Харибда		114,17[32]		Главный пояс — класс C
(34) Цирцея		113,5	1,5	Главный пояс — класс C
Эпиметей Сатурн XI		113,4[3]	0,5304[69]	Спутник Сатурна$
(596) Шейла		113,34[32]		Главный пояс
(56) Мелета		113,24	1,5	Астероид
(129) Антигона		113,0[70]	2	Главный пояс — богата никелем и железом
(12) Виктория		112,8		Главный пояс — класс S
(57) Мнемозина		112,6		Астероид
(545) Мессалина		111,29[32]		Астероид
(2797) Тевкр		111,14[32]		Астероид — троянец Юпитера (L4)
(2920) Автомедон		111,0[32]		Астероид — троянец Юпитера (L4)
2001 QR322		110,0		троянец Нептуна
(91) Эгина		109,8	1,4	Главный пояс — класс C
(140) Жива		109,79[32]	1,4	Главный пояс
(814) Таврида		109,56[32]		Главный пояс
(595) Поликсена		109,07[32]		Главный пояс
(230) Афаманта		108,99	1,36	Главный пояс — класс S
(659) Нестор		108,87[32]		Астероид — троянец Юпитера (L4)
(37) Фидес		108,0	1,3	Главный пояс — класс S
(23) Талия		107,6	1,3	Главный пояс — класс S
(739) Мандевиль		107,53[32]		Главный пояс
2007 VL305		107,5		троянец Нептуна
(40) Гармония		107,2	1,3	Главный пояс — класс S
(181) Эвхарида		106,66[32]	1,2	Главный пояс — класс K
(346) Герментария		106,52[32]		Главный пояс — класс S
(514) Армида		106,17[32]		Главный пояс
(357) Нинина		106,1[32]		Главный пояс
(506) Марион		105,94[32]		Главный пояс — класс C
(365) Кордуба		105,92[32]		Главный пояс — класс C
(36) Аталанта		105,6	1,69	Астероид
(713) Люсциния		105,52[32]		Главный пояс — класс C
(1269) Ролландия		105,19[32]		Главный пояс
(164) Ева		104,87[32]	1,21	Главный пояс — класс C
(98) Ианта		104,5	1,2	Главный пояс — класс C
(240) Ванадида		103,9[32]		Главный пояс — класс C
(221) Эос		103,87[32]	1,17	Главный пояс — класс K
(29981) 1999 TD10		103,7[15]		Транснептуновые объекты
(788) Гогенштейна		103,68[32]		Главный пояс
(791) Ани		103,52[32]		Главный пояс
(1208) Троил		103,34[32]		Астероид — троянец Юпитера (L5)
(192) Навсикая		103,26[32]	1,15	Главный пояс — класс S
(63) Аузониа		103,14	1,1	Главный пояс — класс S
(35) Левкофея		103,11[32]	1,1	Главный пояс — класс C
(570) Китера		102,81[32]		Главный пояс
(233) Астеропа		102,78[32]	1,4	Главный пояс — класс T
(4063) Эвфорбо		102,46[32]		Астероид — троянец Юпитера (L4)
(1583) Антилох		101,62[32]		Астероид — троянец Юпитера (L4)
(1390) Абастумани		101,58[32]		Главный пояс
(522) Хельга		101,22[32]		Главный пояс — семейство Кибелы
(175) Андромаха		101,17[32]	1,08	Главный пояс — класс C
(191) Колга		101,03[32]	1,08	Главный пояс — класс C
(663) Герлинда		100,88[32]		Астероид
(626) Нотбурга		100,73[32]		Астероид
(387) Аквитания		100,51[32]		Главный пояс — класс S
(42) Изида		100,2	1,1	Главный пояс — класс S
(30) Урания		100,0	1,04	Главный пояс — класс S

Объекты диаметром от 40 до 100 км

Астероидов с диаметрами от 100 км и меньше существует несколько тысяч, но лишь немногие из них были более или менее изучены. Массы объектов в этом списке лежат в пределах между 10¹⁵ и 10¹⁸ кг, причём для многих астероидов они носят предполагаемый характер.

Объект	Фото	Средний диаметр, км	Масса, 1015 кг	Тип объекта
(50) ВиргинияA		99,82	1040	Астероид
(114) Кассандра		99,72[32]	1000	Главный пояс — класс T
(1021) Фламмарио		99,39[32]		Астероид
(162) Лаврентия		99,1[32]	1020	Главный пояс
(401) Оттилия		99,12[32]		Главный пояс
ФиваA Юпитер XIV		98,6[3]	430	Спутник Юпитера
(148) Галлия		97,76[32]	980	Главный пояс — класс R
(404) Арсиноя		97,71[32]		Главный пояс — класс C
(27) ЭвтерпаA		96,0	930	Главный пояс — класс S
(773) Ирминтрауд		95,88[32]	1080	Астероид — класс D
(21) Лютеция		95,6[32]	1700[71]	Главный пояс — класс M
(62) Эрато		95,4	910	Главный пояс — семейство Фемиды
(26) Прозерпина		94,8[32]	900	Астероид
(345) Терцидина		94,12[32]		Главный пояс — класс C
ДжульеттаA Уран XI		93,6[3]	560	Спутник Урана
(58) Конкордия		93,44	850	Астероид
(229) Аделинда		93,2[32]		Главный пояс — класс C
Никта		40[72]	70	Спутник Плутона
(103) Гера		91,2	790	Астероид
(17) Фетида		90,0	1200	Астероид
(143) Адрия		89,93[32]	760	Главный пояс
(109) Фелица		89,4	750	Астероид
(100) Геката		89,0[73]	1000	Астероид
(90) Антиопа A		87,8[74]	410	Астероид — класс C — двойной астероид
(227) Философия		87,31[32]		Главный пояс
Прометей $ Сатурн XVI		86,2	156,6	Спутник Сатурна
(110) Лидия		86,1	670	Астероид
ЭлараA Юпитер VII		86,0	870	Спутник Юпитера — Группа Гималии
(72) Ферония		85,9	670	Астероид
(60558) Эхекл/ 174P/Echeclus		84±15[15]		Кентавры[75]
S/2000 (90) 1		83,8[74]		Спутник астероида (90) Антиопа
(71) Ниоба		83,4	610	Астероид
(102) Мириам		83,0[76]		Астероид
(97) Клото		82,8	590	Астероид
(61) Даная		82,04		Астероид
ТалассаA Нептун IV		82,0	350	Спутник Нептуна
(122) Герда		81,7[32]	570	Главный пояс — класс S
(83) Беатрис		81,38	560	Главный пояс
(32) ПомонаA		81,0	550	Астероид
Пандора$ Сатурн XVII		80,6	135,6	Спутник Сатурна
БелиндаA Уран XIV		80,0	360	Спутник Урана
(115) Тира		79,84[32]		Астероид
Крессида Уран IX		79,6[3]	340A	Спутник Урана
(135) Герта		79,24[32]		Астероид
(84) Клио		79,16[77]	520	Астероид
(80) Сапфо		78,4		Астероид
(1001) Гауссия		78,0		Астероид
(58534) Логос		77,0[78]	270	Объект пояса Койпера — кьюбивано — двойной астероид
(124) Алькеста		76,36[32]	470	Главный пояс — класс S
55576 Amycus		76,3[15]		Кентавры
(25) Фокея		75,2		Астероид
(8405) Асбол		74,0[79] — 42[15]		Кентавры
(112) Ифигения		72,7[32]		Астероид
(86047) 1999 OY3		72,0		Объект пояса Койпера — семейство Хаумеа
Гидра		41[72]	391P	Спутник Плутона
Розалинда Уран XIII		72,0	250	Спутник Урана
Калибан Уран XVI		72,0[3]		Спутник Урана
(99) Дике		71,9	390	Астероид
(66) Майя		71,82		Астероид
(116) Сирона		71,7[32]		Главный пояс
(44) Ниса		70,64	370	Главный пояс — класс E
(10370) Хилонома		70[15]		Кентавры
(77) Фригга		69,26	350	Астероид
(55) Пандора		66,7		Астероид
(133) Кирена		66,58[32]	310	Главный пояс — класс S
(79) Эвринома		66,48		Астероид
Наяда Нептун III		66,0	190A	Спутник Нептуна
(43) Ариадна		65,88[32]		Астероид
(101) Елена		65,8	300	Астероид
(108) Гекуба		64,98[80]	390	Астероид
ДездемонаA Уран X		64,0	180	Спутник Урана
Галимеда Нептун IX		62,0		Спутник Нептуна
(52975) Киллар		62,0[15]		Кентавры
(82) Алкмена		60,96		Астероид
(60) Эхо		60,2		Астероид
Комета Хейла — Боппа C/1995 O1		60,0[81]		Комета
Пасифе*A Юпитер VIII		60,0	300	Спутник Юпитера
(7066) Несс		60[15]		Кентавры
Несо Нептун XIII		60,0[3]		Спутник Нептуна
(64) Ангелина		60,0[82]		Главный пояс — класс E
2008 KV42		59,0[83]		Обособленный ТНО
(67) Асия		58,12		Астероид
(119) Алфея		57,3[32]	200	Главный пояс — класс S
(75) Эвридика		55,91[32]	180	Главный пояс — класс M
(142) Пулана		55,29[32]	180	Главный пояс — класс F
(253) Матильда$		52,8	103,3	Главный пояс — класс C
(52872) Окироя		52[15]		Кентавры
Бианка Уран VIII		51,4[36]	92	Спутник Урана
Просперо Уран XVIII		50,0	85	Спутник Урана
Сетебос Уран XIX		48,0[3]	75	Спутник Урана
(4348) Полидамант		48,0[84]		Астероид — троянец Юпитера
(123) Брунхильда		47,97[32]		Главный пояс
(1000) Пиацция		47,78[32]		Главный пояс
(113) Амальтея		46,14[32]	100	Главный пояс
Карме Юпитер XI		46	130	Спутник Юпитера — Группа Карме
(138) Тулуза		45,5[32]	99	Главный пояс — класс S
(126) Веледа		44,8[32]	94	Главный пояс
(73) Клития		44,44	92	Астероид
Сао Нептун XI		44,0		Спутник Нептуна
(125) Либератрикс		43,58[32]	87	Главный пояс — класс M
Метида Юпитер XVI		43,0[54]	36	Спутник Юпитера
(132) Эфра		42,87[32]	82	Главный пояс — класс M
Офелия Уран VII		42,8[3][4]	53	Спутник Урана
Лаомедея Нептун XII		42		Спутник Нептуна
(118) Пейто		41,74[32]	76	Главный пояс
(208) Лакримоза		41,33[32]	73,9	Главный пояс — семейство Корониды — класс S
(136) Австрия		41,0[32]	68	Главный пояс — класс M
(131) Вала		40,44[32]	69	Главный пояс
Корделия* Уран VI		40,2[3]	44	Спутник Урана
Сиарнак Сатурн XXIX		40		Спутник Сатурна

Объекты диаметром от 2 до 40 км

Объект	Фото	Средний диаметр, км	Масса, 1015 кг	Тип объекта
(167) Урда		39,94[32]	66,7	Главный пояс — семейство Корониды — класс S
Синопе* Юпитер IX		38,0	76	Спутник Юпитера
Псамафа* Нептун X		38,0	37	Спутник Нептуна
29P/Швассмана — Вахмана		37,3[15]		Комета — Кентавры
Лиситея* Юпитер X		36,0	63	Спутник Юпитера — Группа Гималии
(158) Коронида		35,37[32]	46,3	Главный пояс — семейство Корониды — класс S
Елена Сатурн XII		35,2[3]	25	Спутник Сатурна
(243) Ида		34,6	42	Главный пояс — семейство Корониды — класс S — двойной астероид
(226) Верингия		33,84[32]		Главный пояс — класс S
(433) Эрос$		33,68	66,9	Околоземные астероиды — амуры
Стефано Уран XX		32,0[3]	22	Спутник Урана
Альбиорикс Сатурн XXVI		32,0		Спутник Сатурна
(1036) Ганимед		31,8	33	Околоземный астероид
(1815) Бетховен		30[85]		Главный пояс
Атлас$ Сатурн XV		30,6	66	Спутник Сатурна
(31824) Элат		30,0[15]		Кентавры
Пердита Уран XXV		30,0[86]	13	Спутник Урана
Пан$ Сатурн XVIII		28,4[87]	4,95[87]	Спутник Сатурна
Линус Каллиопа I		28,0[56]	60[88]	Спутник астероида (22) Каллиопа
Ананке Юпитер XII		28,0[51]	38,2	Спутник Юпитера
Телесто Сатурн XIII или Тетис B		23,6[89]		Спутник Сатурна — троянский спутник Тетиса
Фобос$ Марс I		22,2	10,7	Спутник Марса
Палиак		22,0	8,2	Спутник Сатурна
Франциско Уран XXII		22,0[3]	7,2	Спутник Урана
Калипсо Сатурн XIV или Тетис C		21,4[3]		Спутник Сатурна — троянский спутник Тетиса
Леда Юпитер XIII		20,0[3]	11	Спутник Юпитера — Группа Гималии
Фердинанд Уран XXIV		20,0[3]	5,4	Спутник Урана
Маргарита Уран XXIII		20,0[3]	5,4	Спутник Урана
(149) Медуза		19,76[32]	8	Главный пояс
Ромул		18,0	4	Спутник астероида (87) Сильвия
Имир Сатурн XIX		18,0[3]		Спутник Сатурна
Тринкуло Уран XXI		18,0	3,9	Спутник Урана
Купидон Уран XXVII		18,0	3,8	Спутник Урана
(2002) Эйлер		17,44	5,5	Астероид
Адрастея Юпитер XV		16,4	2	Спутник Юпитера
Кивиок		16,0		Спутник Сатурна
Тарвос Сатурн XXI		15,0		Спутник Сатурна
(2685) Мазурский		15,0	5-11	Астероид
(65407) 2002 RP120		14,6[90]	3,1	Дамоклоиды (ретроградное движение)
Бестла Сатурн XXXIX		14,0		Спутник Сатурна
Маленький принц		13,0	1,2	Спутник астероида (45) Евгения
Деймос$ Марс II		12,4	1,48	Спутник Марса
(951) Гаспра		12,2[91]	2-3	Астероид
Иджирак Сатурн XXII		12		Спутник Сатурна
S/2002 (121) 1		12[92]	1,6	Спутник астероида (121) Гермиона
Комета Галлея		11,0[93]	0,03[94]	Комета (период 75,3 года)
S/2001 (107) 1		11,0[92]	1,5	Спутник астероида (107) Камилла
Маб Уран XXVI		10,0		Спутник Урана
Эррипо Сатурн XXVIII		10,0		Спутник Сатурна
(26858) Мистер Роджерс		9,5		Астероид
Каллирое Уран XVII		8,6		Спутник Юпитера
Гирроккин Сатурн XLIV		8,0		Спутник Сатурна
Фемисто Юпитер XVIII		8,0	0,69	Спутник Юпитера
Дафнис Сатурн XXXV		7,8[87]	0,084[87]	Спутник Сатурна
Рем		7,0	0,2	Спутник астероида (87) Сильвия
Таркек Сатурн LII		7,0		Спутник Сатурна
Кари Сатурн XLV		7,0		Спутник Сатурна
Мундильфари Сатурн XXV		7,0		Спутник Сатурна
Суттунг Сатурн XXIII		7,0		Спутник Сатурна
Праксидике Юпитер XXVII		6,8		Спутник Юпитера
Нарви Сатурн XXXI		6,6		Спутник Сатурна
Скади Сатурн XXVII		6,4		Спутник Сатурна
9P/Темпеля		6,0[95][96]	0,075	Комета
Грейп Сатурн LI		6,0		Спутник Сатурна
Ярнсакса Сатурн L		6,0		Спутник Сатурна
Сколл Сатурн XLVII		6,0		Спутник Сатурна
S/2003 (130) I		6,0	0,4	Спутник астероида (130) Электра
Логи Сатурн XLVI		6,0		Спутник Сатурна
Хати Сатурн XLIII		6,0		Спутник Сатурна
Форньот Сатурн XLII		6,0		Спутник Сатурна
Бефинд Сатурн XXXVII		6,0		Спутник Сатурна
Эгир Сатурн XXXVI		6,0		Спутник Сатурна
S/2007 S 2		6,0		Спутник Сатурна
(118401) LINEAR		6,0	0,23	Комета главного пояса
Бергельмир Сатурн XXXVIII		6,0[3]		Спутник Сатурна
Трюм Сатурн XXX		5,6[97]		Спутник Сатурна
(4179) Таутатис		5,4[98]	0,05	Околоземный астероид
Мегаклите Юпитер XIX		5,4[3] — 2,25[99]		Спутник Юпитера
(2867) Штейнс		5,3[100]		Астероид — класс E
Иокасте Юпитер XXVI		5,2		Спутник Юпитера
Калике Юпитер XXIII		5,2		Спутник Юпитера — Группа Карме
(3200) Фаэтон		5,1	14	Астероид — аполлоны — класс B
Фарбаути Сатурн XL		5,0		Спутник Сатурна
(3753) Круитни		5,0	0,13	Астероид — квазиспутник Земли
Алексгелиос		5,0		Спутник астероида (216) Клеопатра
(5535) Аннафранк		4,8		Астероид
19P/Борелли		4,8[101]		Комета (период 6,85 года)
2P/Энке		4,8		Комета (период 3,3 года)
Тайгете Юпитер XX		4,4		Спутник Юпитера — Группа Карме
Гарпалике Юпитер XXII		4,4		Спутник Юпитера
C/1996 B2 Комета Хякутакэ		4,2[102]		Комета[103]
81P/Вильда		4,0[104]		Комета
Фенрир Сатурн XLI		4,0		Спутник Сатурна
Паллена Сатурн XXXIII		4,0	0,043	Спутник Сатурна
Эвкеладе Юпитер XLVII		4,0		Спутник Юпитера
Гелике Юпитер XLV		4,0		Спутник Юпитера
Аойде Юпитер XLI		4,0		Спутник Юпитера
Гермиппе Юпитер XXX		4,0		Спутник Юпитера
Тионе Юпитер XXIX		4,0		Спутник Юпитера
Автоное Юпитер XXVIII		4,0		Спутник Юпитера
Исоное Юпитер XXVI		3,8		Спутник Юпитера — Группа Карме
Халдене Юпитер XXI		3,8		Спутник Юпитера — Группа Карме
(53319) 1999 JM8		3,5		Астероид
Полидевк Сатурн XXXIV		3,5[105]	0,03	Спутник Сатурна
17P/Холмса		3,4[106]		Комета
Эриноме Юпитер XXV		3,2		Спутник Юпитера — Группа Карме
Мефона Сатурн XXXII		3,2[3]	0,019	Спутник Сатурна
Архе Юпитер XLIII		3,0		Спутник Юпитера
Гегемоне Юпитер XXXIX		3,0		Спутник Юпитера
Эванте Юпитер XXXIII		3,0		Спутник Юпитера
Эвридоме Юпитер XXXII		3,0		Спутник Юпитера
Карпо Юпитер XLVI		3,0	0,45	Спутник Юпитера
Этне Юпитер XXXI		3,0		Спутник Юпитера
(4055) Магеллан		2,49[107]		Астероид — амуры — класс V
(132524) APL		2,3		Астероид
(6178) 1986 DA		2,3	0,002	Астероид — амуры — класс M
Анфа Сатурн LX		2		Спутник Сатурна
Коре Юпитер XLIX		2		Спутник Юпитера
Киллене Юпитер XLVIII		2		Спутник Юпитера
Каллихоре Юпитер XLIV		2		Спутник Юпитера
Мнеме Юпитер XL		2		Спутник Юпитера
Пазифее Юпитер XXXVIII		2		Спутник Юпитера
Кале Юпитер XXXVII		2	0,015	Спутник Юпитера
Спонде Юпитер XXXVI		2		Спутник Юпитера
Ортозие Юпитер XXXV		2		Спутник Юпитера
Тельксиное Юпитер XLII		2		Спутник Юпитера
Эвпорие Юпитер XXXIV		2	0,015	Спутник Юпитера

Объекты диаметром менее 2 км

В главном поясе астероидов по приблизительным оценкам содержится от 1,1 до 1,9 млн астероидов, с размерами, лежащими в диапазоне от 1 до 2 км^[108], а объектов размером менее 1 км многократно больше. В связи с малыми размерами этих астероидов они остаются очень плохо изученными. Исключение составляют лишь те из них, вблизи которых пролетали космические зонды, или которые пролетели мимо Земли на достаточно близком расстоянии, чтобы стать видимыми для крупных земных телескопов.

Часто эти объекты имеют неправильную форму, поэтому здесь указывается средний диаметр астероида. Масса таких объектов — порядка 10¹² кг.

Объект	Фото	Средний диаметр, м	Масса, 1012 кг	Тип объекта
(1620) Географ		1770[32]	4	Околоземный астероид — аполлоны
(1862) Аполлон		1700	5,1	Околоземный астероид — аполлоны — класс Q
Дактиль Ида I		1400		Спутник астероида (243) Ида
(1566) Икар		1400	2,9	Околоземный астероид — аполлоны
(4769) Касталия		1400[109]	0,5	Околоземный астероид — аполлоны
(9969) Брайль		1400		Астероид
(137108) 1999 AN10		1300		Околоземный астероид — аполлоны
(29075) 1950 DA		1200	3	Околоземный астероид — аполлоны
(66391) 1999 KW4		1200	2,33	Меркурий-кроссер — атоны
46P/Виртанена		1200		Комета
103P/Хартли Хартли 2		1140[110]	0,3[110]	Комета (период 6,46 года)
(3908) Нюкта		1040	5	Околоземный астероид — амуры — класс V
S/2003 J 9 Юпитер XXVII		1000[3]		Спутник Юпитера — Группа Карме
S/2003 J 12		1000[3]		Спутник Юпитера
(14827) Гипнос		900[111]		Комета (выродившаяся)[112]
(2062) Атон		900	0,76	Околоземный астероид
2007 CA19		864	1,2	Околоземный астероид
(6489) Голевка		350[113]		Околоземный астероид — аполлоны
(25143) Итокава		692	0,0358	Околоземный астероид
2004 XP14		600		Околоземный астероид
(144898) 2004 VD17		580	3[114]	Околоземный астероид
(4660) Нерей		330[115]		Околоземный астероид
S/2009 S 1 Сатурн LXII		300		Спутник Сатурна
(99942) Апофис		270	0,05[114]	Околоземный астероид
2007 TU24		250[116]		Околоземный астероид
1994 WR12		110[117]	0,002[114]	Околоземный астероид
2008 HJ		36[118]	0,000005[118]	Околоземный астероид — очень быстрое вращение (42 секунды)[118]
1998 KY26		30[119]		Околоземный астероид — очень быстрое вращение (10 минут)
2010 AL30		15—30		Околоземный астероид — период обращения по орбите почти равен одному году[120]; выдвинуто предположение, что это искусственный объект[121]

Стоит обратить особое внимание, что масса астероида 1994 WR₁₂ составляет всего лишь 2⋅10⁹ кг, что даже меньше массы пирамиды Хеопса в Гизе, которая весит 5,9⋅10⁹ кг.

Условные обозначения

^† — указывается экваториальный радиус, исходя из идеально сферической формы тела;

^‡ — указывается средний радиус, полученный усреднением трёх радиусов по основным осям, исходя из приблизительно сферической формы тела;

* — радиус известен лишь очень приблизительно;

^R — радиус тела был определён различными методами, в частности оптическим (Хаббл), инфракрасным (Спитцер) или путём прямого измерения с космических аппаратов;

⁹ — радиус точно неизвестен, но рассчитан из предполагаемого альбедо 0,09;

^$ — подробно изученный астероид или спутник, размеры и масса которого хорошо известны;

^M — масса была определена на основании возмущений, которые создавало/подвергалось тело;

^A — предполагаемая масса

^P — масса рассчитана исходя из предполагаемой плотности Плутона 2,000 г/см³

^O — радиус был определён благодаря покрытию звёзд астероидом.

Гравитация у поверхности

Основным принципом, устанавливающим границы групп, является гравитация, по крайней мере для первых двух групп. Гравитация у поверхности тела на экваторе в большинстве случаев определяется на основе закона всемирного тяготения Ньютона и центробежной силы.

• Ускорение силы тяжести на экваторе определяется на основе закона всемирного тяготения Ньютона и рассчитывается по формуле:

${\displaystyle a_{g}=G{\frac {m}{r^{2}}}}$

где

a_g — величина ускорения свободного падения тела,

G — гравитационная постоянная,

m — масса небесного тела,

r — экваториальный радиус небесного тела или, если он варьируется, то для расчёта используется средний экваториальный радиус.

• Значение центробежной силы или внешнего ускорения, направленного противоположно силе тяжести, рассчитывается по формуле:

${\displaystyle a_{c}=4\pi ^{2}{\frac {r}{T^{2}}}}$

где

T — период вращения небесного тела

• Тогда результирующая сила (сила поверхностной гравитации) будет равна разнице этих двух сил:

${\displaystyle g=a_{g}-a_{c}={\frac {Gm}{r^{2}}}-{\frac {4\pi ^{2}r}{T^{2}}}}$

См. также

• История открытия планет и спутников Солнечной системы
• Список планетоподобных объектов
• Список астероидов