Функция Вейерштрасса

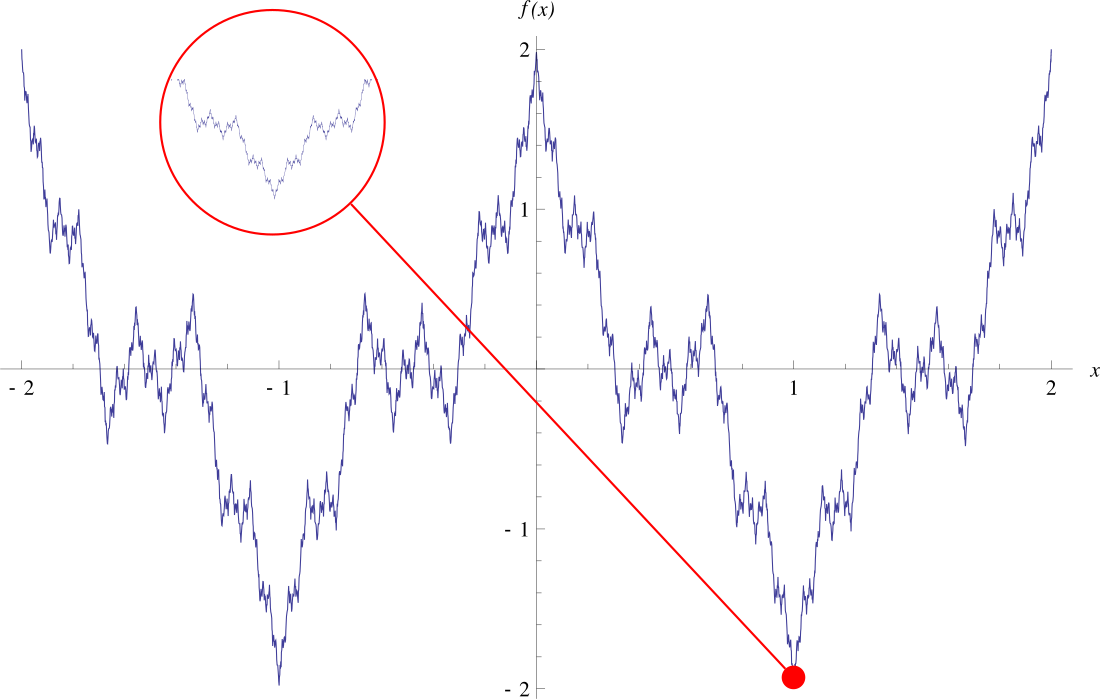
Функция Ве́йерштрасса — пример непрерывной функции, нигде не имеющей производной; контрпример для гипотезы Ампера.

График функции Вейерштрасса с параметрами a = 3, b = 1/2 на интервале [−2, 2]. Этот график имеет фрактальный характер, демонстрируя самоподобие: увеличиваемая область (в красном круге) подобна всему графику.

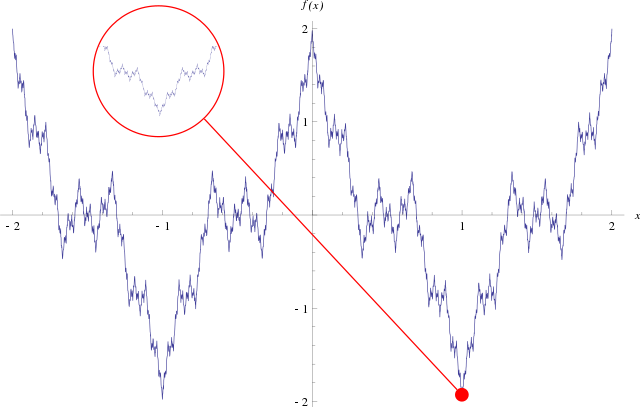
Функция Вейерштрасса задается на всей вещественной прямой единым аналитическим выражением

${\displaystyle w(x)=\sum _{n=0}^{\infty }b^{n}\cos(a^{n}\pi x),}$

где ${\displaystyle a}$ — произвольное нечётное число, не равное единице, а ${\displaystyle b}$ — положительное число, меньшее единицы. Этот функциональный ряд мажорируется сходящимся числовым рядом

${\displaystyle \sum _{n=0}^{\infty }b^{n},}$

поэтому функция ${\displaystyle w}$ определена и непрерывна при всех вещественных ${\displaystyle x}$. Тем не менее, эта функция не имеет производной по крайней мере при

${\displaystyle ab>{\tfrac {3}{2}}\pi +1.}$

Для доказательства отсутствия производной в произвольной точке ${\displaystyle x_{0}}$ строят две последовательности ${\displaystyle \{x_{m}\}}$ и ${\displaystyle \{y_{m}\}}$, сходящиеся к точке ${\displaystyle x_{0}}$, и доказывают, что отношения

${\displaystyle {\frac {w(x_{m})-w(x_{0})}{x_{m}-x_{0}}}}$ и ${\displaystyle {\frac {w(y_{m})-w(x_{0})}{y_{m}-x_{0}}}}$

имеют разные знаки по крайней мере при

${\displaystyle ab>{\tfrac {3}{2}}\pi +1}$ и ${\displaystyle a>1}$.

Указанные последовательности могут быть определены как

${\displaystyle x_{m}={\frac {\gamma _{m}-1}{a^{m}}}}$ и ${\displaystyle y_{m}={\frac {\gamma _{m}+1}{a^{m}}},}$

где ${\displaystyle \gamma _{m}}$ — ближайшее целое число к ${\displaystyle a^{m}x_{0}}$.

Отсутствие производной во всех точках при более общих условиях

${\displaystyle ab\geqslant 1}$ и ${\displaystyle a>1}$

было установлено Харди^[1].

Историческая справка

Запрос «Гипотеза Ампера» перенаправляется сюда. На эту тему нужно создать отдельную статью.

В 1806 году Ампер^[2] предпринял попытку доказать аналитически, что всякая «произвольная» функция дифференцируема всюду, за исключением «исключительных и изолированных» значений аргумента. При этом принималась за очевидное возможность разбиения интервала изменения аргумента на части, в которых функция была бы монотонна. С этими оговорками гипотезу Ампера можно рассматривать как нестрогую формулировку теоремы Лебега^{[англ.][3]}. В первой половине XIX века предпринимались попытки доказать гипотезу Ампера для более широкого класса, именно для всех непрерывных функций. В 1861 году Риман привёл своим слушателям в качестве контрпримера следующую функцию:

${\displaystyle r(x)=\sum \limits _{n=1}^{\infty }{\frac {\sin n^{2}x}{n^{2}}},}$

однако исследование дифференцируемости этой функции чрезвычайно сложно. Джозеф Гервер (англ. Joseph Gerver) доказал, что эта функция всё же имеет производную в некоторых точках, лишь в 1970 году^[4].

В 1872 году Вейерштрасс предложил свой контрпример — описанную выше функцию ${\displaystyle w}$ и представил строгое доказательство её недифференцируемости^[5]. В печати этот пример впервые появился в 1875 году в работе П. Дюбуа-Реймона^[6].

Ещё один пример принадлежит ван дер Вардену (1930):

${\displaystyle v(x)=\sum \limits _{n=0}^{\infty }{\frac {\{10^{n}x\}}{10^{n}}},}$

где фигурные скобки означают взятие дробной части^[7].