Visina trougla

Visina trougla je duž određena vrhom trougla i podnožjem normale spuštene iz tog vrha na naspramnu stranicu trougla.

malo

U svakom trouglu moguće je konstruisati tri visine. Presjek svih visina u trouglu naziva se ortocentar.

To je najkraće rastojanje od vrha do naspramne stranice. Visina se obično obilježava latiničnim slovom ${\displaystyle h}$.

Visina je normalna na tu stranicu, a ta stranica se naziva osnovica. Presjek visine i osnovice naziva se podnožje visine.

Dužina visine je rastojanje između vrha trougla i podnožja visine.

Visina trougla koristiti se za izračunavanje površine trougla, koja je jednaka polovini proizvoda osnovice i visine:

${\displaystyle P={\frac {a\cdot h_{a}}{2}}}$

Visina u različitim vrstama trougla

Visina u pravouglom trouglu

malo

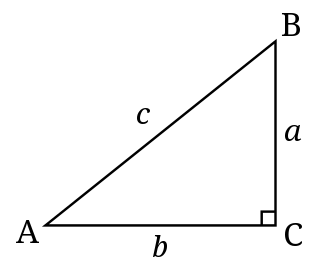
U pravouglom trouglu dvije visine se poklapaju sa katetama, a treća visina dijeli hipotenuzu na odsječke ${\displaystyle p}$ i ${\displaystyle q}$. Formula koja ih povezuje sa visinom koja ih dijeli glasi

${\displaystyle h={\sqrt {pq}}}$ .

Visina u jednakokrakom trouglu

U jednakokrakom trouglu podnožje visine se poklapa sa središtem stranice. U ovom slučaju, visina se poklapa sa simetralom ugla i simetralom stranice.

Ortocentar

Ortocentar trougla je tačka u kojoj se sijeku sve tri visine trougla.

Ortocentar pripada unutrašnjosti trougla ako i samo ako je trougao oštrougli.

U pravouglom trouglu, ortocentar se nalazi u vrhu kod pravog ugla, dok se u tupouglom trouglu ortocentar nalazi izvan trougla.

Ortocentar trougla ima i sledeće osobine.

1. Tačke simetrične ortocentru trougla u odnosu na prave određene stranicama trougla pripadaju kružnici opisanoj oko trougla.
2. Tačke simetrične ortocentru trougla u odnosu na sredine stranica trougla pripadaju kružnici opisanoj oko trougla
3. Rastojanje od tjemena do ortocentra trougla dvaput je veće od rastojanja centra opisane kružnice od naspramne stranice.

Trilinearne koordinate ortocentra

${\displaystyle H={\begin{bmatrix}cos\beta cos\gamma :cos\alpha cos\gamma :cos\alpha cos\beta \end{bmatrix}}}$

Ortocentrični sistem

Ortocentrični sistem je sistem od četiri tačke u ravni - ortocentar trougla (${\displaystyle H}$) zajedno sa sva tri njegova vrha (${\displaystyle A}$, ${\displaystyle B}$ i ${\displaystyle C}$).

Za četiri tačke u ortocentričnom sistemu karakteristično je da je u isto vrijeme svaka od njih ortocentar za trougao koji obrazuju preostale tri tačke kao njegovi vrhovi. Ovako definisana četiri trougla: ${\displaystyle ABC}$, ${\displaystyle ABH}$, ${\displaystyle ACH}$ i ${\displaystyle BCH}$ imaju zajedničku Ojlerovu kružnicu.

Heronova formula

Heronova formula daje obrazac za izračunavanje dužine visine u trouglu poznavanjem dužina sve tri stranice.

U trouglu ${\displaystyle ABC}$ u kojem su dužine stranica ${\displaystyle a}$, ${\displaystyle b}$ i ${\displaystyle c}$, i ${\displaystyle s=(a+b+c)/2}$, visina normalna na stranicu ${\displaystyle a}$ računa se po formuli

${\displaystyle h_{a}={\frac {2{\sqrt {s(s-a)(s-b)(s-c)}}}{a}}}$

Odnosi

${\displaystyle h_{a}=b\sin \gamma =c\sin \beta }$ ${\displaystyle h_{a}={\frac {2P}{a}}}$,

${\displaystyle h_{a}:h_{b}:h_{c}={\frac {1}{a}}:{\frac {1}{b}}:{\frac {1}{c}}=bc:ac:ab}$

${\displaystyle {\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}={\frac {1}{r}}}$,

r radijus upisane kružnoce. ${\displaystyle h_{c}={\frac {1}{2}}{\sqrt {4a^{2}-c^{2}}}}$, gdje je c osnova

${\displaystyle h={\frac {a{\sqrt {3}}}{2}}}$ – za istostranični trougao

Izvori

Треугольники

Značajne tačke i linije u trouglu