Integral
From Wikipedia, the free encyclopedia
Remove ads
Integrál je osnova tako imenovane »višje matematike«, natančneje matematične analize in infinitezimalnega računa.
Temelje integralskega računa sta postavila Isaac Newton in Gottfried Wilhelm Leibniz v poznem 17. stoletju. Integral funkcije je prek osnovnega izreka infinitezimalnega računa povezan z njenim odvodom, določen integral funkcije na nekem intervalu pa je, ko poznamo nedoločenega, moč enostavno izračunati. Integral in odvod sta postala osnovni orodji infinitezimalnega računa, izjemno uporabnega v znanosti in tehniki.
Remove ads
Nedoločeni in določeni integral
Beseda integral zajema dva precej različna pojma:
- Nedoločeni integral dane funkcije f je družina funkcij F, katerih odvod je enak dani funkciji f. V tem smislu je integriranje inverzna operacija kot odvajanje. Rezultat nedoločenega integrala imenujemo primitivna funkcija.
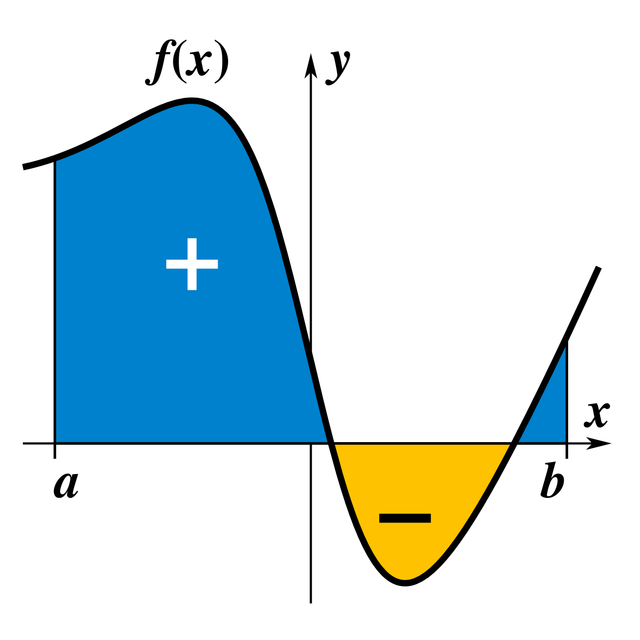
- Določeni integral je povezan s ploščino lika, omejenga z grafom funkcije f. Naj bosta dana pozitivna funkcija f realne spremenljivke x in interval [a, b] na številski premici. Določeni integral funkcije f je ploščina lika, ki ga omejujejo graf funkcije f, os x ter navpični premici x = a in x = b.
Določeni in nedoločeni integral povezuje osnovni izrek infinitezimalnega računa, ki se imenuje tudi Newton-Leibnizova formula: Ploščino omenjenga lika izračunamo tako, da najprej z nedoločenim integralom izračunamo primitivno funkcijo F, potem pa vanjo vstavimo meji intervala: p = F(b) − F(a).
Remove ads
Osnovni izrek infinitezimalnega računa
Osnovni izrek infinitezimalnega računa pravi, da sta si odvajanje in (nedoločeno) integriranje inverzni operaciji: če neko zvezno funkcijo integriramo in nato odvajamo, spet dobimo začetno funkcijo. Pomembna posledica, včasih imenovana drugi osnovni izrek infinitezimalnega računa, omogoča izračun določenega integrala funkcije s pomočjo njenih nedoločenih integralov.
Izreki
- Osnovni izrek infinitezimalnega računa. Naj bo f realna integrabilna funkcija, definirana na zaprtem intervalu [a, b]. Če je F definirana za x na intervalu [a, b] s predpisom
- je F zvezna na intervalu [a, b]. Če je f zvezna v točki x na intervalu [a, b], je F odvedljiva v točki x, in F ′(x) = f(x).
- Drugi osnovni izrek infinitezimalnega računa. Naj bo f realna integrabilna funkcija, definirana na zaprtem intervalu [a, b]. Če je F takšna funkcija, da F ′(x) = f(x) za vsak x na intervalu [a, b] (torej, F je nedoločeni integral funkcije f), potem
- Opomba. Če je f zvezna funkcija na intervalu [a, b], je f odvedljiva na intervalu [a, b], in F, definirana z
- je nedoločeni integral funkcije f na [a, b]. Nadalje
Remove ads
Glej tudi
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads



