Епициклоида

Епициклоида (од грч. -на, над и грч. -круг ) је крива, која се добија када се једна кружница котрља по другој кружници са центром у исходишту и тада произвољна тачка покретне кружнице описује епициклоиду.

Једначина епициклиде

Ако фиксирана кружница има радијус ${\displaystyle R}$, а покретна кружница радијус ${\displaystyle r}$ тада се епициклоида може описивати следећим једначинама:

${\displaystyle x(\theta )=(R+r)\cos \theta -r\cos \left({\frac {R+r}{r}}\theta \right)}$

${\displaystyle y(\theta )=(R+r)\sin \theta -r\sin \left({\frac {R+r}{r}}\theta \right),}$

Пошто између радијуса две кружнице постоји омер ${\displaystyle \textstyle k={\frac {R}{r}}}$ онда се једначине могу написати као:

${\displaystyle x(\theta )=r(k+1)\cos \theta -r\cos \left((k+1)\theta \right)\,}$

${\displaystyle y(\theta )=r(k+1)\sin \theta -r\sin \left((k+1)\theta \right).\,}$

Ако је ${\displaystyle k}$ целобројан онда је епициклоида затворена и има ${\displaystyle k}$ шиљака. У случају да је ${\displaystyle k}$ рационалан број једнак p/q тада епициклоида има p шиљака. У случају да је ${\displaystyle k}$ ирационалан број крива се никада не затвара, па се добија бесконачан број шиљака. Епициклиоида са једним шиљком назива се кардиоида.

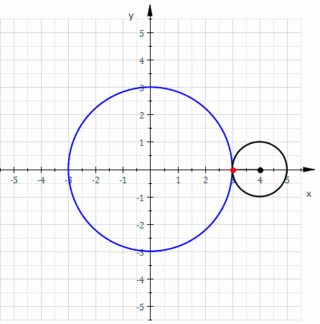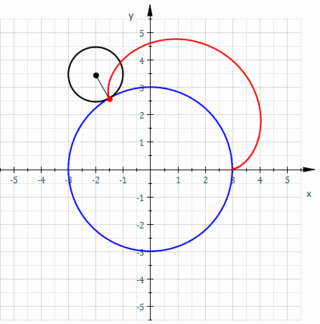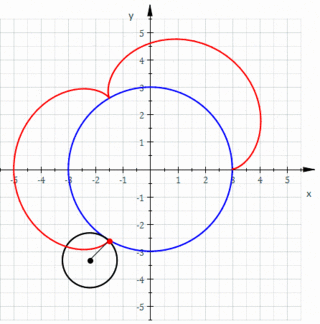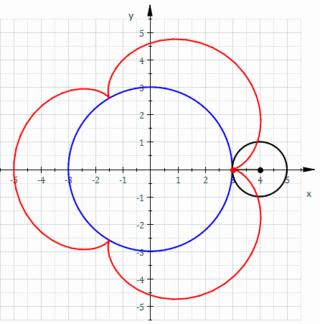
• Epicycloid Examples
• 
  k = 1
• 
  k = 2
• 
  k = 3
• 
  k = 4
• 
  k = 2.1 = 21/10
• 
  k = 3.8 = 19/5
• 
  k = 5.5 = 11/2
• 
  k = 7.2 = 36/5

Доказ

Претпоставимо да желимо да решимо положај тачке ${\displaystyle p}$ и да ${\displaystyle \alpha }$ и ${\displaystyle \theta }$ одговарајући углови приказани на слици. По претпоставци нема клизања између кружница, па вреди:

${\displaystyle \ell _{R}=\ell _{r}}$ тј.

${\displaystyle \ell _{R}=\theta R,\ell _{r}=\alpha r}$, па се добија једначина:

${\displaystyle \theta R=\alpha r}$ и одатле

${\displaystyle \alpha ={\frac {R}{r}}\theta }$

Са слике добија се позиција:

${\displaystyle x=\left(R+r\right)\cos \theta -r\cos \left(\theta +\alpha \right)=\left(R+r\right)\cos \theta -r\cos \left({\frac {R+r}{r}}\theta \right)}$

${\displaystyle y=\left(R+r\right)\sin \theta -r\sin \left(\theta +\alpha \right)=\left(R+r\right)\sin \theta -r\sin \left({\frac {R+r}{r}}\theta \right)}$

Литература

• Епициклоида