Полиедар

Полиедар је геометријско тело омеђено са четири или више многоуглова (који се називају стране или пљоснати полиедри) и коме су ивице дужи. Сама реч је настала као сложеница речи поли (πολυς), што значи много, и речи едрон (εδρον), што значи база, површ, седиште.^[1]

Полиедарска површ

Скуп површи многоуглова таквих да је свака страница сваког многоугла уједно и страница још само једног многоугла, образују затворену површ која се назива полиедарска површ. Део геометријског простора који ограничава (затворена) полиедарска површ је унутрашњост полиедарске површи.

Унија полиедарске површи и њене унутрашњости је полиедар.

• Површи многоуглова, од којих се састоји полиедарска површ, називају се стране (или пљосни) полиедра, а странице тих многоуглова називају се ивице полиедарске површи и полиедра.

• Рогљеви које образују стране полиедра са једним заједничким теменом су рогљеви полиедра, а врхови тих рогљева су темена полиедра.
• Свака дуж која спаја два темена полиедра, а не припада ниједној страни полиедра представља дијагоналу полиедра.
• Свака раван коју одређују три темена полиедра и не садржи ниједну страну полиедра представља дијагоналну раван полиедра.

Подела полиедра

Полиедри могу бити конвексни и неконвексни-конкавни.

• Полиедар је конвексан уколико свака дуж која спаја његове две произвољне тачке припада том полиедру, у супротном случају полиедар је неконвексан односно конкаван.

Конвексни Полиедри

• Конвексан полиедар лежи само са једне стране равни сваке своје стране.
• Конвексан полиедар се може представити као пресек коначног броја полупростора одређених равнима његових страна.

Регуларни полиедри

Полиедар чије су све стране регуларни подударни многоуглови и чији су сви рогљеви подударни назива се регуларан полиедар.

Конвексни регуларни полиедри - Платонова тела

Конвексни регуларни полиедри су познати под називом Платонова тела. Њихове стране су подударни правилни многоуглови, а рогљеви су међусобно подударни и конвексни. То значи да су све стране једног полиедра правилни многоуглови са истим бројем n међусобно једнаких страница и у темену сваког рогља се сустиче исти број k тих многоуглова.

Дуални полиедри

У геометрији полиедри се посматрају у паровима. Сваком полиедру одговара дуални полиедар који настаје метаморфозом датог полиедра у којој:

• сваком темену полазног полиедра одговара страна новог полиедра
• свакој страни полазног полиедра одговара теме новог полиедра
• свакој ивици полазног полиедра одговара ивица новог полиедра.

Особине

• Страна прелази у теме новог полиедра, а њено теме у страну која садржи то теме.
• Теме прелази у страну новог полиедра, а свака страна чије је то теме у теме те стране.
• Ивица која спаја два темена прелази у заједничку ивицу две одговарајуће стране новог полиедра.
• Заједничка ивица две суседне стране полиедра прелази у ивицу која спаја одговарајућа темена новог полиедра.
• Свака страна полиедра је полигон са одређеним бројем својих темена. Метаморфозом полигон прелази у теме, а његова темена у стране новог полиедра чије је то теме, односно страни одовара рогаљ.
• Свако теме полиедра је теме једног његовог рогља. Теме прелази у страну, а стране полиедра које се сустичу у том темену (стране рогља) у темена која припадају тој страни новог полиедра.
• Дуални полиедар дуалног полиедра је полазни полиедар.

Дуални полиедри – Платонова тела

Стране конвексног регуларног полиедра типа {n, k} су правилни полигони са n темена. Страна се пресликава у теме новог полиедра a, а њена темена у стране новог полиедра које се сустичу у том темену. Добија се рогаљ са n страна.

Темена конвексног регуларног полиедра типа су {n, k} су темена подударних рогљева са k страна. Теме рогља прелази у страну, а његове стране (односно стране полиедра које се сустичу у том темену) у k темена те стране новог полиедра.

• Дуални полиедар конвексног регуларног полиедра типа {n, k} је конвексни регуларни полиедар типа {k, n}.

Нумеричке карактеристике Платонових тела

Карактеристика полиедра:

• n – број темена (страница) стране полиедра
• k – број страна које се сустичу у истом темену
• T – број темена полиедра
• S – број страна полиедра
• I – број ивица полиедра

Диедар чине две суседне стране са заједничком ивицом која представља ивицу диедра. Сви диедрални углови једног Платоновог тела су међусобно једнаки. Диедрални угао се очитава у равни нормалној на ивицу диедра.

Тетраедар (види анимацију)

Размотана фигура тетраедра

Платонова тела - тетраедар

• 4 темена
• 6 ивица
• 4 стране
• Диедрални угао: 70.53°

Формуле

Површина	${\displaystyle P={\sqrt {3}}a^{2}}$
Запремина	${\displaystyle V={\begin{matrix}{1 \over 12}\end{matrix}}{\sqrt {2}}a^{3}}$
Полупречник описане сфере	${\displaystyle r_{o}\,=\,{\frac {\sqrt {6}}{4}}\,a\approx 0{,}61\,a}$
Полупречник уписане сфере	${\displaystyle r_{u}\,=\,{\frac {\sqrt {6}}{12}}\,a\approx 0{,}20\,a}$
Висина	${\displaystyle h=r_{o}+r_{u}\,=\,{\frac {\sqrt {6}}{3}}\,a\,=\,{\sqrt {\frac {2}{3}}}\,a\approx 0{,}82\,a}$
Угао између ивице и површи	${\displaystyle arctg{\sqrt {2}}\approx 55^{\circ }}$
Угао између две површи	${\displaystyle \arccos {1/3}=arctg2{\sqrt {2}}\approx 71^{\circ }}$

Платонова тела – хексаедар

Коцка

• 8 темена
• 12 ивица
• 6 страна
• Диедрални угао: 90°

Формуле

Важнији елементи коцке

Површина	${\displaystyle S=6a^{2}\,}$
Запремина	${\displaystyle V=a^{3}\,}$
Мала дијагонала[2]	${\displaystyle d_{1}=a{\sqrt {2}}}$
Велика дијагонала	${\displaystyle d_{2}=a{\sqrt {3}}}$
Полупречник уписане сфере	${\displaystyle r_{u}={\frac {a}{2}}}$
Полупречник описане сфере	${\displaystyle r_{o}={\frac {d_{2}}{2}}=a{\frac {\sqrt {3}}{2}}}$

Платонова тела – октаедар

Октаедар

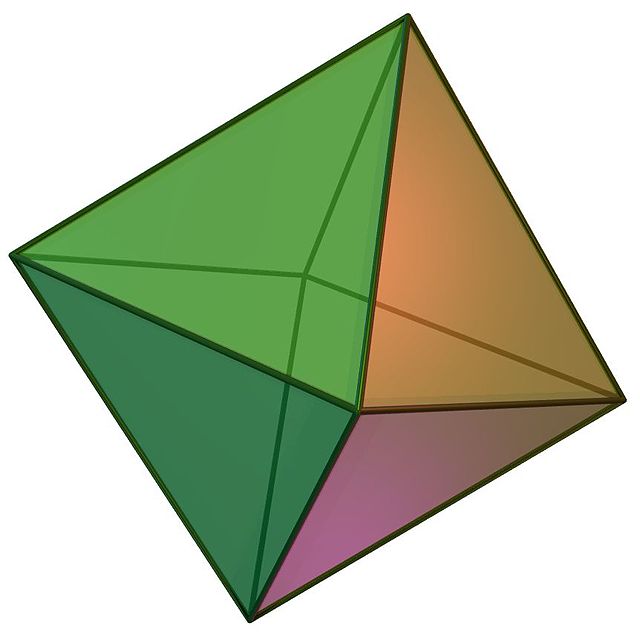
• 6 темена
• 12 ивица
• 8 страна
• Диедрални угао: 109.47°

Формуле

Површина	${\displaystyle S=2{\sqrt {3}}a^{2}}$
Запремина	${\displaystyle V={\frac {\sqrt {2}}{3}}a^{3}}$
Полупречник описане сфере	${\displaystyle r_{o}={\frac {\sqrt {2}}{2}}a}$
Полупречник уписане сфере	${\displaystyle r_{u}={\frac {\sqrt {6}}{6}}a}$

Платонова тела – додекаедар

Додекаедар

• 20 темена
• 30 ивица
• 12 страна
• Диедрални угао: 116.56°

Формуле

Површина	${\displaystyle S=3{\sqrt {25+10{\sqrt {5}}}}\,a^{2}}$
Запремина	${\displaystyle V={\frac {1}{4}}\left(15+7{\sqrt {5}}\right)a^{3}}$
Полупречник уписане сфере	${\displaystyle r_{u}={\frac {\sqrt {5}}{20}}{\sqrt {50+22{\sqrt {5}}}}\,a}$
Полупречник описане сфере	${\displaystyle r_{o}={\frac {\sqrt {3}}{4}}\left(1+{\sqrt {5}}\right)\,a}$

Платонова тела – икосаедар

Икосаедар

• 12 темена
• 30 ивица
• 20 страна
• Диедрални угао: 138.19°

Формуле

Површина	${\displaystyle P=5{\sqrt {3}}a^{2}}$
Запремина	${\displaystyle V={\frac {5}{12}}\left(3+{\sqrt {5}}\right)a^{3}}$
Полупречник уписане сфере	${\displaystyle r_{u}={\frac {a}{12}}{\sqrt {3}}\left(3+{\sqrt {5}}\right)}$
Полупречник описане сфере	${\displaystyle r_{o}={\frac {a}{4}}{\sqrt {10+2{\sqrt {5}}}}}$

Изометрија полиедра

Узајамно једнозначно пресликавање f: T1 → T2 полиедара (тела) T1, T2 у коме долази до очувања метрике односно очувања растојања између тачака је изометрично пресликавање или изометрија. Геометријске трансформације: транслација, ротација, рефлексија и њихова композиција (узастопно извођење) у произвољном поретку и произвољном броју су изометричне трансформације.

Симетрије полиедра

Изометрично пресликавање f : T → T полиедара T у самог себе је симетрија. Група симетрија сваког полиедра садржи све могуће ротације и све могуће рефлексије које полиедар пресликавају у самог себе. Композиција симетрија једног полиедра (у произвољном поретку) је такође једна симетрија из групе свих могућих симетрија тог полиедра.