Topološko uređenje

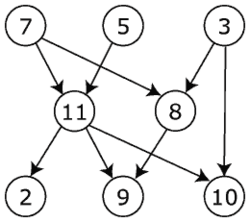
U informatici, topološko sortiranje (skraćeno topsort ili toposort) ili topološko uređenje usmerenog grafa je linearno uređenje njegovih čvorova tako da svaka usmerena grana UV od čvora U ka čvoru V, U dolazi pre V u uređenju. Na primer, čvorovi grafa predstavljaju zadatke koje treba izvršiti, a grane predstavljaju ograničenja da neki zadataka mora biti izvršen pre nekog drugog; u ovoj aplikaciji, topološko uređenje je samo validan raspored izvršavanja zadataka. Topološko uređenje je moguće, ako i samo ako graf nema usmerene cikluse, odnosno da je usmereni acikličan graf (UAG). Svaki UAG ima najmanje jedno topološko uređenje, i poznat je algoritam za konstruisanje topološkog uređenja bilo kog UAG u linearnom vremenu.

Primeri

Kanonska aplikacija topološkog sortiranja (topološkog uređenja) je u planiranju rasporeda poslova ili zadata na osnovu njihove zavisnosti; algoritmi topološkog sortiranja su prvi put proučavani ranih 1960-ih godina u kontekstu PERT tehnike planiranja upravljanja projektima (^[1]). Poslovi su predstavljeni čvorovima i postoji grana od A ka B, ako posao A mora biti izvršen pre nego što se posao B može zapoceti (primer: kod pranja veš mašine, mašina mora da završi sa pranjem veša da bi ga mi satvili na sušenje). Dakle, topološko sortiranje nam daje redosled kojim treba da izvršavamo poslove.

U informatici, aplikacije ovog tipa prerastaju u instrukcije organizacije, uređenju formula ćelija evaluacije pri reizračunavanju formula valuacije u tabelama, logičke sinteze, određivanje rasporeda zadataka kompilacije koji se izvršavaju u mejkfajlovima, serijalizaciji podataka i određivanju zavisnosti simbola u linkerima.

Graf prikazan sa leve strane se može na mnogo načina topološki sortirati, uključujući: 7, 5, 3, 11, 8, 2, 9, 10 (vuzuelno sa leva na desno, sa vrha ka dnu) 3, 5, 7, 8, 11, 2, 9, 10 (prvo čvorovi sa najmanjom vrednošću) 3, 7, 8, 5, 11, 10, 2, 9 5, 7, 3, 8, 11, 10, 9, 2 (najkrace grane prvo) 7, 5, 11, 3, 10, 8, 9, 2 (prvo čvorovi sa največom vrednošću) 7, 5, 11, 2, 3, 8, 9, 10

Algoritmi

Uobičajeni algoritmi sa topološkim sortiranjem imaju linearnu složenost po broju grana plus broju čvorova (${\displaystyle O(\left|{V}\right|+\left|{E}\right|)}$).

Jedan od ovih algoritama, koji je opisao Kahn 1962, radi tako što odabira čvorove u istom redosledu kao i eventualno topološko sortiranje.Prvo nade listu „početnih čvorova“ koji nemaju ulazne grane i ubacuje ih u S; barem jedan takav čvor mora postojati u acikličnom grafu. Zatim:

L ← Prazna lista koja će sadržati sortirane elemente
S ← Skup svih čvorova bez ulaznih grana
while S is non-empty do
    remove a node n from S
    insert n into L
    for each node m with an edge e from n to m do
        remove edge e from the graph
        if m has no other incoming edges then
            insert m into S
if graph has edges then
    return error (Graf ima bar jedan ciklus)
else 
    return L (Topološki sortirani)

Ako je graf UAG, rešenje ce se nalaziti u listi L(rešenja ne moraju biti jedinstvena). U suprotnom, graf ima bar jedan ciklus i topološko sortiranje se ne može uraditi.

Napomenimo da, zbog ne-jedinstvenosti rezultata sortiranja, struktura S može biti jednostavno skup, red ili stek.U zavisnosti od redosleda kojim se čvorovi n izbacuju iz skupa S, dobijamo različita rešenja.Varijacije Kahn-ovog algoritma koji razbije veze leksikografskih oblika, ključna je komponenta Kafman-Grahamovog algoritma za paralelno planiranje i slojevito crtanje grafa.

Alternativni algoritam za topološko sortiranje je zasnovan na pretraživanju u dubinu.Kod ovog algoritma, grane su usmerene u suprotnom smeru od prethnog algoritma(a u suprotnom smeru nego sto su prikazane na dijagramu uznad). Postoji grana od A ka B ako posao A zavisi od posla B(ako posao B mora biri izvršen pre nego sto posao A može da se započne). Algoritam se kreće kroz svaki čvor grafa, u proizvoljnom redosledu, započinjući pretragu u dubinu koja se zaustavlja kada se dođe do čvora koji je već posećen.

L ← Prazna lista koja će sadržati sortirane čvorove
while there are unmarked nodes do
    select an unmarked node n
    visit(n) 
function visit(čvor n)
    if n has a temporary mark then stop (nije UAG)
    if n is not marked (nije posećen) then
        mark n temporarily
        for each node m with an edge from n to m do
            visit(m)
        mark n permanently
        add n to head of L

Primetimo da se svaki čvor n dodaje u izlaznu listu L tek nakon što se razmotre svi čvorovi od kojih n zavisi(svi potomci čvora n u grafu).Posebno, kada algoritam doda čvor n, zagarantovano je da su svi čvorovi od kojih zavisi n već dodati u izlaznu listu L:dadati su u L ili prethodnim rekurzivnim pozivom visit() ili ranijim pozicom visit(). Kako su svi čvorovi i svaka grana posećeni jednom, algoritam se izvršava u linearnom vremenu. Ovaj algoritam, zasnovan je na pretrazi u širinu, opisao ga je Cormen et al. 2001, ali ga je pre njega opisao Tarjan 1976 u stampi.

Složenost

• Računarska kompleksnost izračunavanja u usmerenom grafu je NC²; što znači da se može izračunati za O(log² n) vremena na paralelnom računaru pomoću polinomijalnog broja od O(n^k)procesora, za istu konstantu k^[2].

Jedinstvenost

Kada bi topološko sortiranje imalo osobinu da sve parove uzastopnih čvorova u sortiranom poretku poveže granama, dobili bismo usmeren Hamiltonov put u UAG. Ako Hamiltonov put postoji, topološki poredak je jedinstven; nijedan drugi poredak ne zadovoljava ivice puta.Obrnuto, ako topološko sortiranje ne formira Hamiltonov put, UAG će imati dva ili više validna topološka poretka, jer je u ovom slučaju uvek moguće formirati drugi ispravan poredak zamenom dva uzastopna čvora koji nisu povezani granom. Dakle, moguće je proveriti u linearnom vremenu da li postoji jedinstveni poredak, i da li postoji Hamiltonov put, uprkos NP-težini problema Hamiltonovog puta za neke opštije usmerene grafove^[3].

Odnos prema relaciji poretka

Topološka sortiranja su usko povezana sa konceptom lineanog istezanja relacije poretka u matematici.

Parcijalno uredjen skup je skup objekata sa definicijom relacije manje ili jednako "≤", zadovoljavajući aksiome refleksivnosti(x ≤ x), antisimetričnosti(ako je x ≤ y i y ≤x onda je x = y), i tranzitivnosti (ako je x ≤ y i y ≤ z, onda je x ≤ z).Relacija totalnog poretka je relacija poretka u kojoj su svaka dva objekta x i y iz skupa uporedivi, ili je x ≤ y ili je y ≤ x.Totalna uređenja se koriste u informatici kako bi operatori poređenja mogli da izedu upoređivanje kod algoritama za sortiranje.Za konačne skupove, totalna uređenja se mogu identifikovati kao linearan niz objekata gde je "≤" relacija tačna kad god prvi objekat prethodi drugom u redu;algoritmi za sortiranje upoređivanjem se mogu iskoristiti za pretvaranje totalnog uređenja u niz na ovaj način. Linearno istezanje relacije poretka je totalni poredak koji je usaglašen sa njim, u smislu ako je x ≤ y u relaciji poretka onda je i x ≤ y u totalnom poretku takođe.

Može se definisati relacija poretka iz bilo kog DAL-a tako što ćemo postaviti da skup objekata budu čvorovi DAL-a i definišemo da je x ≤ y tačno za bilo koja dva čvora x i y', kad god postoji usmeren put od x ka y,tj. kad god iz x možemo da stignemo do y. Ovako definisano, topološko uređenje DAL-a je isto što i linearno istezanje ove relacije poretka. Obrnuto, svaka relacija poretka može biti definisana kao relacija domašaja u DAL-u. Jedan način da se ovo izvede je da se definiše DAL koje ima čvor za svaki objekat iz skupa relacije poretka i granu xy za svaki par objekata za koje važi x ≤ y. Alternativan način da se uradi ovo je da se koristi tranzitivno zatvorenje relacije poretka;u celini, ovako dobijamo DAL-ove sa manje grana ali je relacija domašaja i dalje ista relacija poretka. Ovako se algoritmi za topološko sortiranje mogu koristiti za nalaženje linearnih istezanja relacije poretka.

Vidi još

• tsort, Јуникс програм за тополошко сортирање