Hipoteza (matematika)

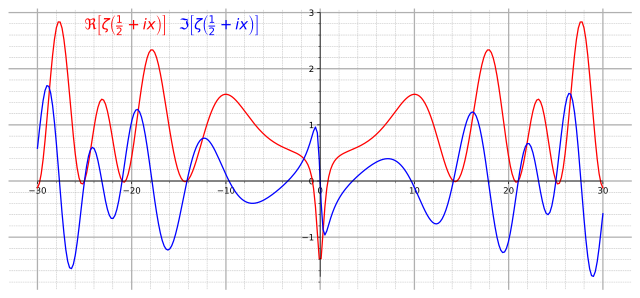
U matematici, hipoteza je zaključak ili predlog za koji se pretpostavlja da je istinit zbog preliminarnih pratećih dokaza, ali za koji još nije pronađen dokaz ili opovrgnuće.^[1][2][3][4] Neke konjekture, kao što je Rimanova hipoteza (još uvek pretpostavka) ili poslednja Fermaova teorema (pretpostavka koju je Endru Vajls dokazao 1995. godine), oblikovali su veći deo matematičke istorije, jer su razvijena nova područja matematike kako bi se dokazale.^[5]

Realni deo (crveno) i imaginarni deo (plavo) Rimanove zeta funkcije duž kritične linije = 1/2. Prve netrivijalne nule mogu se videti kod = ±14,135, ±21,022 i ±25,011. Rimanova hipoteza je poznata hipoteza, kaže da sve netrivijalne nule zeta funkcije leže duž kritične linije.

Važni primeri

Poslednja Fermaova teorema

Glavni članak: Poslednja Fermaova teorema

U teoriji brojeva, Poslednja Fermaova teorema (ponekad zvana Fermaova konjektura, posebno u starijim tekstovima) navodi da nijedna tri pozitivna cela broja ${\displaystyle a}$, ${\displaystyle b}$, i ${\displaystyle c}$ ne mogu da zadovolje jednačinu ${\displaystyle a^{n}+b^{n}=c^{n}}$ za bilo koju celobrojnu vrednost ${\displaystyle n}$ veću od dva.

Ovu teoremu je prvi formulisao Pjer de Ferma 1637. godine na marginama kopije Diofantove Aritmetike, gde je tvrdio da ima dokaz koji je prevelik da bi stao u marginu.^[6] Prvi uspešan dokaz objavio je Endru Vajls 1994. godine, a formalno je objavljen 1995. godine, nakon 358 godina napora matematičara. Ovaj nerešeni problem podstakao je razvoj algebarske teorije brojeva u 19. veku, i dokaz teoreme modularnosti u 20. veku. Ovo je jedna je od najistaknutijih teorema u istoriji matematike, a pre njenog dokaza bila je u Ginisovoj knjizi svetskih rekorda kao jedan od „najtežih matematičkih problema”.^[7]