Функција расподеле

Функција расподеле, функција дистрибуције или кумулативна расподела вероватноће је функција у теорији вероватноће у ознаци која за сваки реалан број , одређује вероватноћу да је случајна променљива узела вредност мању од или једнаку :

${\displaystyle x\to F_{X}(x)=\operatorname {P} (X\leq x).}$

За означавање функције расподеле обично се користи велико латинично слово , за разлику од малог латиничног слова , које се користи за расподелу вероватноће.

Кумулативна расподела вероватноће се може изразити и преко расподеле вероватноће на следећи начин^[1]:

${\displaystyle F(x)=\int _{-\infty }^{x}f(t)\,dt.}$

Вероватноћа да лежи на интервалу за је једнака .

Својства

Одозго надоле, функција расподеле дискретне случајне променљиве, непрекидне случајне променљиве, и случајне променљиве која има и непрекидне и дискретне делове.

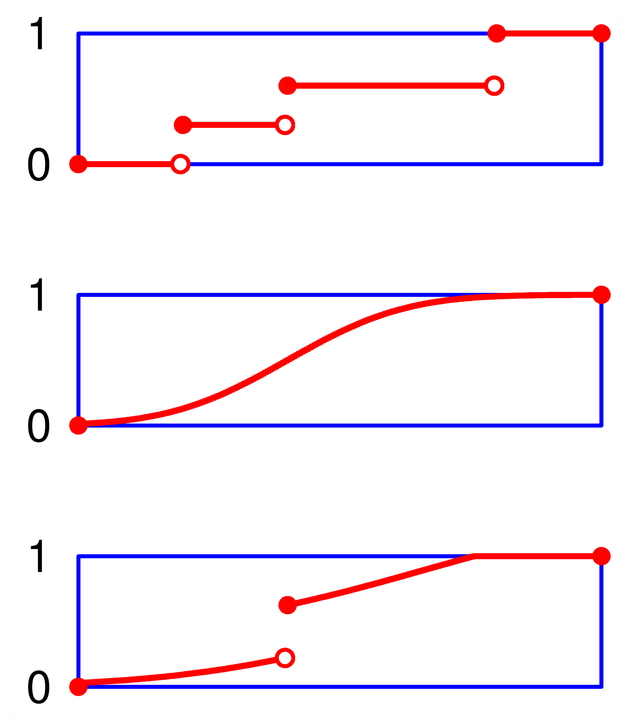
Свака функција расподеле, има следеће особине:

• монотоно је неопадајућа
• непрекидна је здесна
• ${\displaystyle \lim _{x\to -\infty }F(x)=0}$
• ${\displaystyle \lim _{x\to +\infty }F(x)=1.}$

Дискретне случајне променљиве

Ако је дискретна случајна променљива која узима вредности ₁, ₂, ... са вероватноћама , њена функција расподеле ће имати прекиде у тачкама , и бити константна између њих:

${\displaystyle F(x)=\operatorname {P} (X\leq x)=\sum _{x_{i}\leq x}\operatorname {P} (X=x_{i})=\sum _{x_{i}\leq x}p(x_{i}).}$

Континуалне случајне променљиве

Ако је функција расподеле , случајне променљиве , непрекидна, онда је непрекидна случајна променљива; ако је осим тога, апсолутно непрекидна, онда постоји Лебег-интеграбилна функција , таква да

${\displaystyle F(b)-F(a)=\operatorname {P} (a\leq X\leq b)=\int _{a}^{b}f(x)\,dx}$

за све реалне бројеве и . (Прва од горње две једнакости не би била тачна у општем случају ако не би било назначено да је расподела непрекидна. Непрекидност расподеле имплицира да је , па разлика између < и ≤ у том контексту нема значаја.) Функција је једнака изводу од скоро свуда, и назива се расподела вероватноће за случајну променљиву .

Види још

• Расподела вероватноће