Optimizacija roja čestica

U računarskoj nauci, optimizacija roja čestica (particle swarm optimization, PSO)^[1] je računarski metod koji optimizuje problem iterativnim pokušajem da se poboljša rešenje kandidata s obzirom na datu meru kvaliteta. On rešava problem tako što ima populaciju kandidata rešenja, ovde nazvanih česticama, i pomera ove čestice u prostoru za pretragu prema jednostavnoj matematičkoj formuli preko položaja i brzine čestice. Kretanje svake čestice je pod uticajem njene lokalne najbolje poznate pozicije, ali je takođe vođeno ka najpoznatijim pozicijama u prostoru za pretragu, koje se ažuriraju kako bolje pozicije pronalaze druge čestice. Očekuje se da će to pomeriti roj ka najboljim rešenjima.

Roj čestica koji traži globalni minimum funkcije.

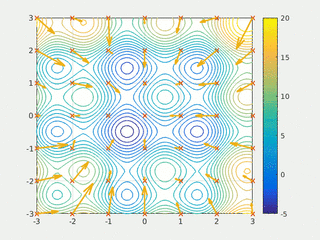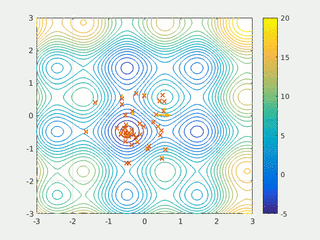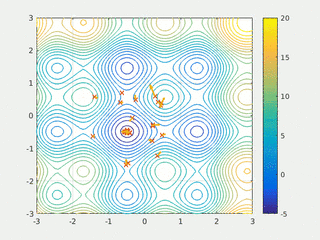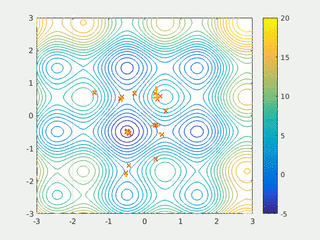
PSO se prvobitno pripisuje Kenediju, Eberhartu i Šiju^[2][3] i inicijalno je bio namenjen simulaciji društvenog ponašanja,^[4] kao stilizovani prikaz kretanja organizama u jatu ptica ili jatu riba. Algoritam je pojednostavljen i primećeno je da vrši optimizaciju. Knjiga Kenedija i Eberharta^[5] opisuje mnoge filozofske aspekte PSO i inteligencije roja. Poli je napravio opsežnu anketu o PSO aplikacijama.^[6][7] Godine 2017, Bonjadi i Mihalevič su objavili sveobuhvatan pregled teorijskih i eksperimentalnih radova o PSO.^[1]

PSO je metaheurističan jer daje malo ili nimalo pretpostavki o problemu koji se optimizuje i može pretraživati veoma velike prostore rešenja kandidata. Takođe, PSO ne koristi gradijent problema koji se optimizuje, što znači da PSO ne zahteva da problem optimizacije bude diferencibilan kao što se zahteva klasičnim metodama optimizacije poput gradijentnog spuštanje i kvazi-njutnovske metode. Međutim, metaheuristika kao što je PSO ne garantuje da će se ikada naći optimalno rešenje.