உட்கணம்

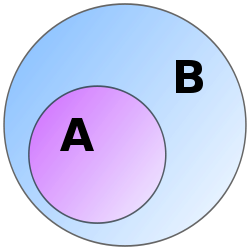
கணிதத்தில், குறிப்பாகக் கணக் கோட்பாட்டில், A என்னும் ஒரு கணத்தின் உறுப்புகள் அனைத்தும் B என்னும் இன்னொரு கணத்தில் அமைந்திருந்தால், A கணமானது B இன்உட்கணம் (Subset) என்று வழங்கப்படும். சமானமாக, B கணமானது A கணத்தின் மேற்கணம் அல்லது மிகை கணம் (superset) எனப்படும். A , B ஆகிய இரு கணங்களும் ஒன்றிடனொன்று ஒன்றலாம்.

B இன் தகு உட்கணம் A; மறுதலையாக A இன் தகு மேற்கணம் B என்பதை விளக்கும் ஆய்லர் வரைபடம்.

${\displaystyle A\subseteq B}$ எனில், ${\displaystyle \forall x\left(x\in A\Rightarrow x\in B\right).}$^[1]

உட்கண உறவானது கணங்களின் மீது ஒரு பகுதி வரிசையை (partial order) வரையறுக்கும். உட்கணங்களின் இயற்கணிதமானது, உட்கண உறவை ”உள்ளடக்கலாகக்” (inclusion) கருதும் பூலிய இயற்கணிதத்தை உருவாக்கும்.

வரையறை

பொதுவாகக் கணம் என்பது நன்கு வரையறுக்கப்பட்ட பொருள்களின் தொகுப்பைக் குறிக்கும். உட்கணமும் ஒரு கணத்தையே குறிக்கும். B என்பது ஒரு வெற்றற்ற கணம் என்க. அதில் A என்பது B யின் உட்கணம் எனில், A யில் உள்ள ஒவ்வொரு உறுப்பும் B யின் உறுப்பாகும். மாறாக, B ஆனது A யின் மிகைக் கணம் அல்லது மேற்கணம் எனவும் அழைக்கலாம்.

A இன் உறுப்பு ஒவ்வொன்றும் B இன் உறுப்பாகவும் இருந்தால், A என்பது B இன் உட்கணம் என வரையறுக்கப்படுகிறது.

இதன் குறியீடு:

${\displaystyle A\subseteq B}$,

இதற்குச் சமானமாகப் B என்பது Aஇன் மிகைக் கணம் அல்லது மேற்கணம் எனவும் வரையறுக்கப்படும்.

குறியீடு:

${\displaystyle B\supseteq A.}$

வெற்றுக் கணம் (${\displaystyle \{\}}$ அல்லது ${\displaystyle \varnothing ,}$), உறுப்புகளற்ற கணம் என்பதால் அது எந்தவொரு கணம் X க்கும் உட்கணமாக இருக்கும்.

பண்புகள்

A ⊆ B ; B ⊆ C எனில் A ⊆ C

• ஒரு முடிவுறு கணம் A , மற்றுமொரு கணம் B இரண்டின் வெட்டு கணத்தின் எண்ணளவையும், A இன் எண்ணளவையும் சமமாக இருந்தால், இருந்தால் மட்டுமே, A ஆனது B இன் உட்கணமாக இருக்கும். அதாவது,

${\displaystyle A\subseteq B\Leftrightarrow |A\cap B|=|A|}$ என இருந்தால், இருந்தால் மட்டுமே, ${\displaystyle A\subseteq B}$ ஆகும்.

• A ⊆ B ; B ⊆ C எனில் A ⊆ C ஆக இருக்கும்.

⊂ , ⊃ குறியீடுகள்

உட்கணம் மற்றும் மிகைக்கணம் இரண்டையும் குறிப்பதற்குச் சில நூலாசிரியர்கள் ⊊ and ⊋ என்பவற்றுக்குப் பதில் ⊂ , ⊃ என்ற குறியீடுகளைப் பயன்படுத்துகின்றனர்.^[2] எடுத்துக்காட்டாக, இவர்களைப் பொறுத்தவரை ஒவ்வொரு கணம் A க்கும், A ⊂ A.

வேறுசிலர் தகு உட்கணம், தகு மிகைக்கணம் இரண்டையும் குறிப்பதற்கு ⊊ , ⊋ குறிகளுக்குப் பதில் முறையே ⊂ , ⊃ இரண்டையும் பயன்படுத்துகின்றனர்.^[3]

எடுத்துக்காட்டுகள்

ஒழுங்கு பல்கோணிகளின் கணமானது பல்கோணிகள் கணத்தின் உட்கணமாக அமையும்

• A = {1, 2} ஆனது B = {1, 2, 3} இன் தகு உட்கணமாகும். எனவே A ⊆ B , A ⊊ B என்ற இரு குறியீடுகளுமே உண்மையாகும்.
• D = {1, 2, 3} ஆனது E = {1, 2, 3} இன் உட்கணமாகும். எனவே D ⊆ E உண்மை; D ⊊ E உண்மையில்லை.
• எந்தவொரு கணமும் தனக்குத்தானே உட்கணமாக இருக்கும், ஆனால் தகு உட்கணமாக இருக்காது. (X ⊆ X என்பது உண்மை, ஆனால் X ⊊ X உண்மையில்லை.)
• எந்தவொரு கணத்துக்கும் வெற்றுக் கணம் (∅) ஒரு உட்கணமாக இருக்கும். வெற்றுக்கணமானது தன்னைத் தவிரப் பிற கணங்கள் அனைத்திற்கும் தகு உட்கணமாக இருக்கும்.
• {x: x ஒரு பகா எண்; x > 10} என்பது {x: x ஒரு ஒற்றையெண்; x > 10} என்ற கணத்தின் தகு உட்கணமாகும்.
• இயல் எண்களின் கணமானது விகிதமுறு எண்களின் கணத்தின் தகு உட்கணமாகும்;கோட்டுத்துண்டிலுள்ள புள்ளிகளின் கணமானது ஒரு கோட்டின் மீதமைந்த புள்ளிகளின் கணத்தின் தகு உட்கணமாகும். இவ்விரு எடுத்துக்காட்டுகளிலும் முழு கணங்களும் உட்கணங்களும் முடிவிலி கணங்களாகவும் சமமான எண்ணளவைகள் கொண்டவையாகவும் இருக்கும்.
• ஆய்லர் படத்தில் மற்றுமொரு எடுத்துக்காட்டு:

• 
  A ஆனது B இன் தகு உட்கணம்
• 
  C ஆனது B இன் உட்கணம், ஆனால் தகு உட்கணமல்ல.

மேற்கோள்கள்

1. Rosen, Kenneth H. (2012). Discrete Mathematics and Its Applications (7th ed.). New York: McGraw-Hill. p. 119. பன்னாட்டுத் தரப்புத்தக எண் 978-0-07-338309-5.
2. Walter Rudin (1987), Real and complex analysis (3rd ed.), New York: McGraw-Hill, p. 6, பன்னாட்டுத் தரப்புத்தக எண் 978-0-07-054234-1, MR 0924157
3. Subsets and Proper Subsets (PDF), archived from the original (PDF) on 2013-01-23, பார்க்கப்பட்ட நாள் 2012-09-07

• Jech, Thomas (2002). Set Theory. Springer-Verlag. பன்னாட்டுத் தரப்புத்தக எண் 3-540-44085-2.

வெளியிணைப்புகள்

• Weisstein, Eric W., "Subset", MathWorld.