கோடு (வடிவவியல்)

வடிவவியலில் கோடு (அல்லது நேர்கோடு)(Line) என்பது கணக்கிடமுடியாத அளவுக்கு (தோராயமாக முடிவிலிக்குச் சமமாக) மிகச் சன்னமானதும் மிக நீளமானதுமான ஒரு வடிவவியல் உருவம் அல்லது பொருளாகும். அதாவது நீளமானதும் நேரானதுமான வளைகோடு, நேர் கோடு ஆகும். ஒரு நேர்கோட்டை வரையறுக்க இரண்டு புள்ளிகள் தேவை. அந்த இரண்டு புள்ளிகளுக்கு இடையேயான குறைந்த பட்ச தூரத்தின் பாதையில் நேர்கோடு அமையும். இரு கோடுகள் அதிக பட்சம் ஒரு புள்ளியில் தான் வெட்டி கொள்ள முடியும். இரு தளங்கள் அதிக பட்சம் ஒரு நேர்கோட்டில் தான் வெட்டி கொள்ள முடியும்.^[1][2][3][4]

நேர்கோடுகள்

வளைகோடு (வ), நேர்க்கோடு (நே), மடிக்கோடு (ம) காட்டப்பட்டுள்ளன.

ஓர் ஒப்பச்சுச் சட்டத்தில் பல நேர்க்கோடுகளும் அதன் சமன்பாடுகளும் காட்டப்பட்டுள்ளன. காட்டாக, சிவப்புக் கோட்டைக் குறிக்கும் சமன்பாட்டில் x = 0 என்று கொண்டால், y-வெட்டு மதிப்பாக y = 1 என்பது கிடைப்பதைப் படத்தில் காணலாம்.

நேர்க்கோடு (நேர்கோடு) என்பது எல்லா இடத்திலும் ஒரே சாய்வு கொண்டுள்ள ஒரு கோடு. இடத்திற்கு இடம் சாய்வு மாறாது. துல்லியமாய் வரையறை செய்கையில், ஒரு நேர்க்கோடு என்பது பருமன் ஏதும் அற்ற ஒரே சாய்வோடு முழுநீளமும் நேராக இருக்கும் ஒரு கோடு. யூக்கிளிடின் வடிவவியல் கணிதத்தின் படி எந்த இரு புள்ளிகளின் வழியாகவும் ஒரே ஒரு நேர்க்கோடு மட்டுமே செல்லும். எந்த இரு புள்ளிகளுக்கும் இடையே உள்ள மிகக்குறைந்த இணைப்பு, தொலைவு அல்லது நீளப் பாதை ஒரு நேர்க்கோடுதான்.

நேர்க்கோட்டிற்கான கணித சமன்பாட்டு வழி விளக்கம்

ஓரு கார்ட்டீசியன் ஒப்பச்சுச் சட்டத்தில் வரையப்பட்ட எந்த ஒரு நேர்க்கோட்டையும் செயற்கூறு வழி ஒரு சமன்பாட்டால் விளக்கலாம்:

${\displaystyle y=mx+b\,}$

மேலே உள்ள பொதுச் சமன்பாட்டில்:

m என்பது நேர்க்கோட்டின் சாய்வைக் குறிக்கும்.

b என்பது நேர்க்கோடு நெடுக்கு அச்சை (y-அச்சை) வெட்டும் தொலவு y-வெட்டு

x என்பது கிடை அச்சின் (x-அச்சின்) வழி அளக்கப்படும் சாரா மாறி.

y என்பது சார் மாறியால் மாறும் செயற்கூறு.

மேற்கூறிய சமன்பாட்டில்:

x என்னும் சார்பற்ற மாறி சுழியாக இருந்தால் ( x = 0), y = b.

y = 0, என்றால், x = -b/m = x-வெட்டு.

m = - ( y-வெட்டு) / (x-வெட்டு) .

ஆகவே சாய்வு எனப்படுவது, கிடையாக x தொலைவு சென்றால், நேர்க்கோடானது எவ்வளவு உயர்கின்றது ( y அளவு என்ன) என்பதைக் குறிக்கும்.

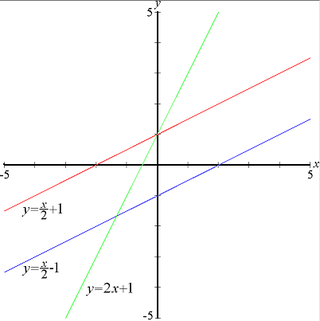
இக்கருத்துக்களைப் படத்தில் வரைந்து காட்டியுள்ள பல நேர்க்கோடுகளையும் அதற்கான சமன்பாடுகளையும் கொண்டு புரிந்து கொள்ளலாம்.

நேர்கோட்டு சமன்பாடுகள்

பொதுச் சமன்பாடு

நேர்கோட்டுச் சமன்பாட்டின் பொது வடிவம்:

${\displaystyle Ax+By+C=0}$,

இங்கு A, B இரண்டும் ஒரே சமயத்தில் பூச்சியமாக இருக்காது.

இரு புள்ளிகள் வழி சமன்பாடு

(x₁, y₁) மற்றும் (x₂, y₂) என்ற இரு புள்ளிகள் வழிச் செல்லும் நேர்கோட்டின் சமன்பாடு:

f(x) = y₁ + [(y₂ - y₁) / (x₂ - x₁)](x - x₁),

இங்கு x₁ மற்றும் x₂ வெவ்வேறாவவை. இவை சமமாக இருந்தால் சமன்பாடு பின்வருமாறு எளியதொன்றாகி விடும்.

${\displaystyle x=x_{1}}$

இப்பொழுது, இரண்டாவது புள்ளிக்கு அவசியமில்லாமல் போய்விடுகிறது.

சாய்வு - புள்ளி சமன்பாடு

${\displaystyle (a,b)}$ என்ற புள்ளி வழியே செல்வதும் சாய்வு(Slope) ${\displaystyle m}$ கொண்டதுமான நேர்கோட்டின் சமன்பாடு:

${\displaystyle y=m(x-a)+b}$.

சாய்வு - வெட்டுத்துண்டு சமன்பாடு

சாய்வு m மற்றும் y -வெட்டுத்துண்டு(Intercept) b

${\displaystyle y=mx+b}$.

வெட்டுப்புள்ளி - வெட்டுப்புள்ளி சமன்பாடு

நேர்கோடானது x -அச்சை (a, 0) -புள்ளியிலும் y -அச்சை (0, b) -புள்ளியிலும் சந்தித்தால் அதன் சமன்பாடு.

${\displaystyle x/a+y/b=1}$,

இதனை,

${\displaystyle xb+ya=ab}$ எனவும் எழுதலாம். a மற்றும் b பூச்சியமாக இருந்தாலும் இவ்வடிவில் கணக்கிடுதல் சாத்தியமாகும்.

மேலும் பார்க்க

• கோட்டுத்துண்டு
• வளைகோடு
• இயங்குவரை
• ஒரு புள்ளியிலிருந்து ஒரு கோட்டின் தூரம்
• தளம்
• பல்கோண வளைவரை