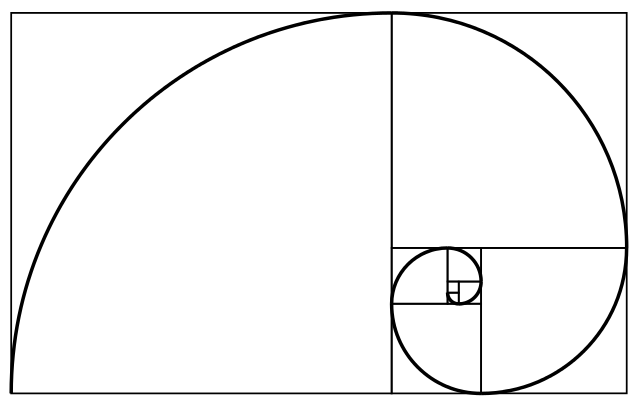
Золота спіраль

Золота спіраль — логарифмічна спіраль, швидкість зростання якої дорівнює φ — золотій пропорції

Наближена і справжня спіралі за числами Фібоначчі: зелена спіраль складена з четвертинок кіл всередині квадратів, в той час як червона спіраль є золотою спіраллю, особливим типом логарифмічної спіралі. Місця, де спіралі накладаються одна на одну, показано жовтим кольором. Довжина частини спіралі всередині більшого квадрата відноситься до довжини спіралі всередині наступного квадрата згідно правила золотого перетину

Золота спіраль.
Якщо довжина сторони квадрата дорівнює 1, то наступний менший квадрат має сторони довжиною 1/φ. Наступні — 1/φ², 1/φ³ і так далі.

Золоті спіралі є самоподібними. Їхня форма ідеально повторюється при збільшенні.

Формула

Рівняння для золотої спіралі в полярній системі координат таке ж саме, що і для інших логарифмічних спіралей, але зі спеціальним значенням коефіцієнта зростання b:

${\displaystyle r=ae^{b\theta }}$,

або:

${\displaystyle \theta ={\frac {1}{b}}\ln(r/a)}$,

де e — основа натуральних логарифмів, a — довільна позитивна дійсна константа, а b знаходиться з рівняння:

${\displaystyle e^{\frac {\pi b}{2}}\,=\varphi }$,

в якому ${\displaystyle \varphi ={\frac {{\sqrt {5}}+1}{2}}}$ — золотий перетин. Рішенням цього рівняння є:

${\displaystyle b={\frac {2\ln {\varphi }}{\pi }}\approx 0{,}306349}$.

Оскільки спіраль може йти як за годинниковою стрілкою, так і проти неї, b може бути і негативним:

Спіраль Фібоначчі апроксимує золоту спіраль з використанням четвертинок кола в квадратах з розмірами квадратів, що дорівнюють числам Фібоначчі. На малюнку показані квадрати з розмірами 1, 1, 2, 3, 5, 8, 13, 21 34.

${\displaystyle b=\pm {\frac {2\ln {\varphi }}{\pi }}\approx \pm 0{,}306349}$.

Альтернативною формулою для золотої спіралі є:

${\displaystyle r=ac^{\theta }}$,

де константа c задається формулою:

${\displaystyle c=e^{b}=\varphi ^{\frac {2}{\pi }}\approx 1{,}358456}$.

Наближення золотої спіралі

Литовська монета

Існує кілька схожих спіралей, які наближені, але не збігаються в точності з золотою спіраллю, з якою їх часто плутають.

Наприклад, золоту спіраль можна апроксимувати, почавши з прямокутника, у якого відношення між довжиною і шириною дорівнює золотій пропорції (такий прямокутник називають золотим). Цей прямокутник можна розділити на квадрат і подібний йому прямокутник, його, своєю чергою, розділити тим же чином, і продовжувати цей процес довільну кількість разів. Тоді ми отримаємо майже повне розкладання прямокутника на квадрати. Кути цих квадратів можна з'єднати четвертинками кіл, і тоді ми отримаємо криву, яка хоч і не є справжньою логарифмічною спіраллю, але близько її апроксимує.

Ще однією апроксимацією є спіраль Фібоначчі, яка будується подібно до вищеописаної спіралі, за винятком того, що починають з прямокутника з двох квадратів і додають потім до більшої сторони прямокутника квадрат такої ж довжини. Оскільки відношення між сусідніми числами Фібоначчі наближається до золотої пропорції, спіраль все більше наближається до золотої спіралі в міру додавання квадратів (див. другий малюнок).

Спіралі у природі

Наближення до логарифмічних спіралей трапляється в природі (наприклад, рукави спіральних галактик чи раковини молюсків). Золоті спіралі є окремим випадком логарифмічних спіралей. Недавній глибокий аналіз спіралей, що зустрічаються в роговичному епітелії мишей, показав, що трапляються як золоті, так й інші логарифмічні спіралі. Іноді трапляються твердження, що спіральні галактики й раковини наутилідів частіше трапляються у формі золотої спіралі тому, що золота спіраль пов'язана із золотим перетином і послідовністю Фібоначчі, однак насправді спіральні галактики й раковини молюсків часто мають вигляд логарифмічних спіралей, які істотно відрізняються від золотої.

Див. також

• Золотий кут
• Золотий прямокутник

Інтернет-ресурси

Німецькою

• Marcus Frings: Goldener Schnitt. In: RDK. Labor (2015).

Англійською

• Marcus Frings: The Golden Section in Architectural Theory. In: Nexus Network Journal, 2002, 4/1.
• Weisstein, Eric W. Golden Ratio(англ.) на сайті Wolfram MathWorld.
• Джон Дж. О'Коннор та Едмунд Ф. Робертсон. The Golden Ratio в архіві MacTutor (англ.)
• Alexander Bogomolny: Golden Ratio. cut-the-knot.org
• Steven Strogatz: Proportion Control. New York Times (Online), 24. September 2012.
• послідовність A001622 з Онлайн енциклопедії послідовностей цілих чисел, OEIS (Dezimalentwicklung von ${\displaystyle \Phi }$), послідовність A028259 з Онлайн енциклопедії послідовностей цілих чисел, OEIS (Engel-Entwicklung von ${\displaystyle \Phi }$), послідовність A118242 з Онлайн енциклопедії послідовностей цілих чисел, OEIS (Pierce-Entwicklung von ${\displaystyle 1/\Phi }$).