Коваріантність і контраваріантність (математика)

У Вікіпедії є статті про інші значення цього терміна: Коваріантність і контраваріантність.

Коваріантність і контраваріантність — поняття, які використовуються в математиці (лінійній алгебрі, диференціальній геометрії, тензорному аналізі) і у фізиці, для опису того, як тензори (скаляри, вектори, оператори, білінійні форми тощо) змінюються при перетвореннях базисів у відповідних просторах або многовидах. Контраваріантними називають «звичайні» компоненти, які при зміні базису простору змінюються за допомогою перетворення, зворотного до перетворення базису. Коваріантними — ті, які змінюються так само, як і базис.

     вектор v, описаний в термінах

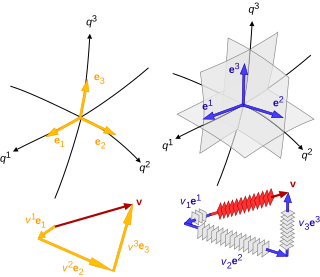
дотичного базиса

     e₁, e₂, e₃ в      координатних кривих (ліворуч),

дуального базиса, ковекторного базиса або взаємного базиса

     e¹, e², e³ в      координатних поверхнях (праворуч),

в 3-d загальних криволінійних координатах (q¹, q², q³), кортеж чисел для визначення точки в координатному просторі. Зверніть увагу, що базис і кобазіс збігаються тільки тоді, коли базис ортогональний.^[1]

Зв'язок між коваріантними і контраваріантними координатами тензора можливий тільки в просторах, де заданий метричний тензор (не слід плутати з метричним простором).

Терміни коваріантність і контраваріантність були введені Сильвестром в 1853 році для досліджень з алгебричної теорії інваріантів.