Радикал Брінга

Радикал Брінга чи ультрарадикал від дійсного числа ${\displaystyle \ a}$ це єдиний дійсний корінь многочлена

${\displaystyle x^{5}+x+a.}$

Графік функції радикала Брінга для дійсного аргумента

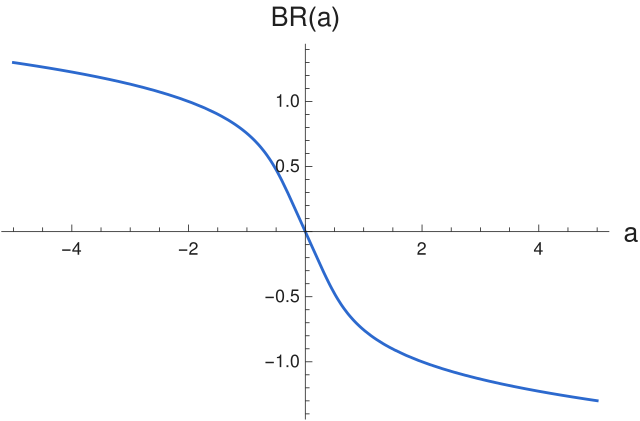
Позначається ${\displaystyle \operatorname {BR} (a).}$ Для дійсного аргумента, це спадна необмежена непарна функція, з асимптотою для великих значень ${\displaystyle \mathrm {BR} (a)\sim -a^{1/5}}$.

Джордж Жерард показав, що рівняння п'ятого степеня можуть бути розв'язані у закритій формі використовуючи радикали та Брінгові радикали, які були введені Ерландом Брінгом.

Нормальні форми рівняння п'ятого степеня

Загальна форма рівняння п'ятого степеня:

${\displaystyle x^{5}+a_{4}x^{4}+a_{3}x^{3}+a_{2}x^{2}+a_{1}x+a_{0}=0.\,}$

Існують різні методи спрощення, що використовують перетворення Чірнхауса скорочення ненульових коефіцієнтів:

Первинна форма

Форма без 4-го степеня та куба:

${\displaystyle y^{5}+c_{2}y^{2}+c_{1}y+c_{0}=0\,}$

називається первинною і може бути отримана квадратичним перетворенням Чірнхауса, що пов'язує корені загальної і первинної форм

${\displaystyle y_{k}=x_{k}^{2}+\alpha x_{k}+\beta \,,}$

коефіцієнти α та β можуть бути отримані з результанта чи тотожностей Ньютона.

Форма Брінга—Жерарда

Можливо також занулити коефіцієнт при квадраті, це форма Брінга—Жерарда:

${\displaystyle v^{5}+d_{1}v+d_{0}=0.\,}$

Кубічне перетворення Чірнхауса не допомагає, бо приводить до рівняння 6-го степеня.

Але в 1786 році Брінг знайшов перетворення Чірнхауса 4-го степеня:

${\displaystyle v_{k}=y_{k}^{4}+\alpha y_{k}^{3}+\beta y_{k}^{2}+\gamma y_{k}+\delta \,.}$

що приводить до системи 5 рівнянь з 6 невідомими, де потрібно розв'язувати кубічні і квадратні рівняння. Цей метод також був відкритий Джорджем Жерардом в 1832.

Таку систему краще розв'язувати в одній із систем комп'ютерної алгебри, оскільки запис розв'язку є незрівнянно довшим за розв'язок рівняння четвертого степеня.

Далі лінійною заміною змінної можна звести до форми від одного коефіцієнта:

${\displaystyle u^{5}-u+a=0\,,}$

яка використовується в методах розв'язку Ерміта—Кронекера—Брілші, Глассера, Коклі—Харлі з різними резольвентами.

Загальний розв'язок рівняння 5-го ступеня

Корені многочлена

${\displaystyle x^{5}+px+q\,}$

Можуть бути отримані використовуючи радикал Брінга:

${\displaystyle {\sqrt[{4}]{-{\frac {p}{5}}}}\,\operatorname {BR} \left(-{\frac {1}{4}}\left(-{\frac {5}{p}}\right)^{\frac {5}{4}}q\right)}$

Джерела

• Hazewinkel, M. (2001), transformation Tschirnhausen transformation, у Hazewinkel, Michiel (ред.), Математична енциклопедія, Springer, ISBN 978-1-55608-010-4
• Weisstein, Eric W. Bring–Jerrard Quintic Form(англ.) на сайті Wolfram MathWorld.
• Weisstein, Eric W. Bring Quintic Form(англ.) на сайті Wolfram MathWorld.
• Weisstein, Eric W. Ultraradical(англ.) на сайті Wolfram MathWorld.