Реберне покриття

Ребе́рне покриття́ графа — це множина ребер C, така, що кожна вершина графа інцидентна принаймні одному ребру з C.

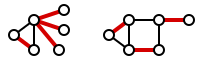
На малюнку показано реберне покриття двох графів.

Найме́нше ребе́рне покриття́ — це реберне покриття найменшого розміру. Число ребер у найменшому реберному покритті графа називають число́м ребе́рного покриття́ і позначають ${\displaystyle \rho (G)}$ (в книзі Свамі, Тхулалірамана — ${\displaystyle \beta _{1}(G)}$). На малюнку показано приклади найменших реберних покриттів.

Зауважимо, що покриття правого графа є не тільки реберним покриттям, але й паруванням. Більш того, це парування є досконалим паруванням — у ньому кожна вершина відповідає рівно одному ребру парування. Досконале парування (якщо існує) завжди є найменшим реберним покриттям.

Задача пошуку найменшого реберного покриття є задачею оптимізації, яка належить до класу задач покриття^[en] і може бути розв'язана за поліноміальний час.

Приклад

• Якщо в графі немає ізольованих вершин (тобто вершин степеня 0), то множина всіх ребер є реберним покриттям (але не обов'язково найменшим!). Якщо ізольовані вершини є, реберного покриття в цьому графі не існує.
• Повний двочастковий граф K_m,n має число реберного покриття max(m, n).

Властивості

• Згідно з другою тотожністю Галлаї, в графі без ізольованих вершин загальне число ребер у найменшому реберному покритті і найбільшому паруванні дорівнює числу вершин графа.

Алгоритм

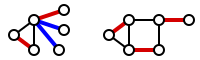
Найменше реберне покриття можна знайти за поліноміальний час, знайшовши найбільше парування і додавши за допомогою жадібного алгоритму ребра для покриття решти вершин^[1][2]. На малюнку найбільше парування показано червоним кольором. Додаткові ребра, додані для покриття непокритих вершин, показано синім кольором (у графі праворуч найбільше парування є досконалим паруванням, у якому всі вершини вже покриті, так що немає потреби в додаткових ребрах.)

Див. також

• Задача про вершинне покриття
• Задача про покриття множини — задача про реберне покриття є окремим випадком задачі про покриття множини е лементами генеральної сукупності є вершини, а кожна підмножина покриває рівно два елементи.