Сортування гребінцем

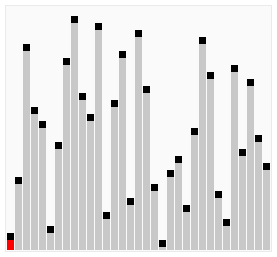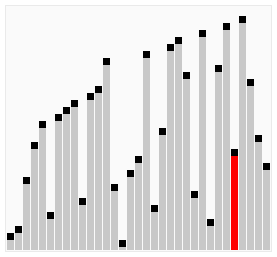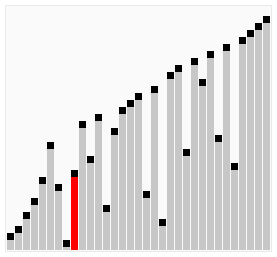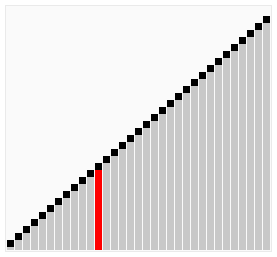
Сортування гребінцем (англ. Comb sort) — спрощений алгоритм сортування, розроблений Влодеком Добошєвічем (Wlodek Dobosiewicz) у 1980 році. Пізніше його заново дослідили та популяризували Стефан Лакей (Stephen Lacey) та Річард Бокс (Richard Box), які опублікували статтю про нього в журналі «Byte Magazine» у квітні 1991 р. Сортування гребінцем є поліпшенням алгоритму сортування бульбашкою, і конкурує за швидкодію з швидке сортування. Основна його ідея полягає в тому, щоб усунути так званих «черепах», або малих значень ближче до кінця списку, оскільки у сортування бульбашкою вони сильно уповільнюють процес сортування. (Кролики та великі сортування на початку списку у сортуванні бульбашкою не являють собою проблеми).

Сортування гребінцем

Клас	Алгоритм сортування
Структура даних	масив
Найгірша швидкодія	${\displaystyle \Omega (n^{2})}$[1]
Найкраща швидкодія	${\displaystyle O(n)}$
Середня швидкодія	${\displaystyle \Omega (nlogn)}$
Просторова складність у найгіршому випадку	О(n) загальний, O(1) допоміжний
Оптимальний	Так

У сортуванні бульбашкою, коли два елементи порівнюються, вони завжди мають розрив (відстань один від одного) рівну 1. Основна ідея сортування гребінцем полягає у тому, що цей розрив може бути більший одиниці. (Алгоритм Сортування Шелла також базується на даній ідеї, однак, він є модифікацією алгоритму сортування включенням, а не сортування бульбашкою).

Розрив починається зі значення, що рівне довжині списку, поділеного на фактор зменшення (зазвичай, 1.3; див. нижче), і список сортується з урахуванням цього значення (при необхідності воно заокруглюється до цілого). Потім розрив знову ділиться на фактор розриву, і список продовжує сортуватись з новим значенням, процес продовжується доти, доки розрив рівний 1. Далі список сортується з розривом рівним 1 доти, доки не буде повністю відсортований. Таким чином, фінальний етап сортування аналогічний такому ж у сортуванні бульбашкою, однак, до цього «черепахи» усуваються.

Фактор зменшення

Фактор зменшення справляє великий ефект на швидкість алгоритму сортування гребінцем. В оригінальній статті, автор пропонує значення 1.3 після багатьох експериментів з іншими значеннями.

Текст описує процес вдосконалення алгоритму використовуючи значення ${\displaystyle 1/\left(1-{\frac {1}{e^{\varphi }}}\right)\approx 1.247330950103979}$ як фактор зменшення. Вона також мість приклад використання алгоритму на псевдокоді.

Приклади реалізації на різних мовах програмування

Псевдокод

function combsort11(array input)
    gap := input.size

    loop until gap > 1 and swaps = 1
        if gap > 1
            gap := gap / 1.3
        end if
        

        i := 0
        swaps := 0
        

        loop until i + gap <= input.size
            if input[i] > input[i+gap]
                swap(input[i], input[i+gap])
                swaps := 1
            end if
            i := i + 1
        end loop
       

    end loop
end function

C

int newGap(int gap)
{
    gap /= 1.3;
    if (gap < 1)
        return 1;

    return gap;
}

void combSort(int* a, int len)
{
    int gap = len;
    bool swapped = true;

    while (gap > 1 || swapped)
    {
        swapped = false;
        gap = newGap(gap);

        for (int i = 0; i < len - gap; ++i)
        {
            if (a[i] > a[i + gap])
            {
                swap(a[i], a[i + gap]);
                swapped = true;
            }
        }
    }
}

Java

private static int newGap(int gap)
{
        gap = gap * 10 / 13;
        if(gap < 1)
                return 1;

        return gap;
}

private static void sort(int a[])
{       int gap = a.length;
        boolean swapped;

        do {
                swapped = false;
                gap = newGap(gap);

		for(int i = 0; i < (a.length - gap); i++) {
			if(a[i] > a[i + gap]){
		        	swapped = true;
                                int temp = a[i];
                                a[i] = a[i + gap];
                                a[i + gap] = temp;
                        }
                }
        } while(gap > 1 || swapped);
}

Python

def update_gap(gap):
    gap = (gap * 10) / 13
    if gap == 9 or gap == 10:
        gap = 11
    return max(1, gap)

def combsort(x):
    gap = len(x)
    swapped = True
    if gap < 2:
        return
    while gap > 1 or swapped:
        gap = update_gap(gap)
        swapped = False
        for i in range(0, len(x) - gap, gap):
            if x[i] > x[i + gap]:
                x[i], x[i + gap] = x[i + gap], x[i]
                swapped = True

Див. також

• Сортування бульбашкою
• Сортування змішуванням