Теорема Брамагупти

Теоре́ма Брамагу́пти (англ. Brahmagupta's Theorem) — теорема елементарної геометрії про одну з властивостей вписаного у коло чотирикутника, доведена у сьомому столітті нашої ери індійським математиком Брамагуптою і носить його ім'я^[1].

Формулювання теореми

${\displaystyle {\overline {BD}}\perp {\overline {AC}},{\overline {EF}}\perp {\overline {BC}}}$ ${\displaystyle \Rightarrow |{\overline {AF}}|=|{\overline {FD}}|}$

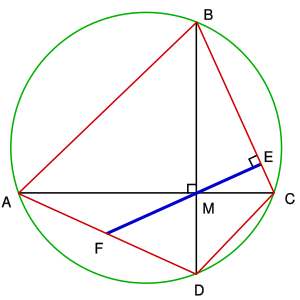
Основне формулювання теореми^[2]:

Якщо вписаний у коло чотирикутник має взаємно перпендикулярні діагоналі, які перетинаються у точці ${\displaystyle M}$, то пряма, що проходить через точку ${\displaystyle M}$ і є перпендикулярною до однієї з його сторін, ділить протилежну до неї сторону навпіл.

Примітка По аналогії із серединним перпендикуляром (медіатрисою) до сторони трикутника відрізок FE на рисунку праворуч називають антимедіатрисою протилежних сторін чотирикутника. З урахуванням цієї примітки теорема Брамагупти може бути сформульована у вигляді:

Якщо вписаний у коло чотирикутник має перпендикулярні діагоналі, що перетинаються у точці ${\displaystyle M}$, то дві пари його антимедіатрис проходять через точку ${\displaystyle M}$.

Доведення теореми

На рисунку зображено вписаний чотирикутник ${\displaystyle ABCD}$, що має перпендикулярні діагоналі ${\displaystyle AC}$ і ${\displaystyle BD}$, а пряма ${\displaystyle ME}$ є перпендикулярною до сторони ${\displaystyle BC}$ й перетинає сторону ${\displaystyle DA}$ у точці ${\displaystyle F}$. Тоді

${\displaystyle \angle {DMF}=\angle {BME}=\angle {MCE}\equiv \angle {ACB}=\angle {ADB}\equiv \angle {FDM}.}$

Отже, трикутник ${\displaystyle FMD}$ є рівнобедреним.

Аналогічно, рівнобедреним буде і трикутник ${\displaystyle FAM}$. Тому ${\displaystyle |FA|=|FM|=|FD|}$.

Див. також

• Формула Брамагупти