五复合正四面体

在几何学中，五复合正四面体是一种由五个正四面体组合成的几何图形^[3]，属于星形二十面体^[4]，也是唯一五种正复合体之一^[5]，其索引编号为UC₅。温尼尔在他的书中列出了许多星形多面体模型，其中也收录了五复合正四面体，并将之给予编号W₂₄^[6]。其也收录于哈罗德·斯科特·麦克唐纳·考克斯特的书《五十九种二十面体》中，编号为47^[7]，但这个多面体最早是由埃德蒙·赫斯在1876年发现并描述的。

五复合正四面体

（单击查看旋转模型）
类别	复合正多面体 星形二十面体
对偶多面体	五复合正四面体
识别
名称	五复合正四面体
参考索引	UC5, W24
数学表示法
考克斯特符号 （英语：Coxeter-Dynkin diagram）	{5,3}[5{3,3}] {3,5}[2]
性质
体	5
面	20
边	30
顶点	20
欧拉特征数	F=20, E=30, V=20 （χ=10）
组成与布局
复合几何体数量	5
复合几何体种类	5个正四面体
面的种类	20个正三角形
对称性
对称群	手性（英语：Chirality (mathematics)）二十面体群（英语：Icosahedral symmetry） (I)
旋转对称群 （英语：Rotation_groups）	手性（英语：Chirality (mathematics)）四面体群（英语：Tetrahedral symmetry） (T)
图像
星状图（英语：Stellation_diagram） 星状（英语：Stellation）核 凸包 正二十面体 正十二面体

性质

五复合正四面体为五个正四面体组合成的形状，由于没有顶点共用的情况，因此其边、面和顶点的数量为正四面体的5倍，共有20个面、30条边和20个顶点。

结构

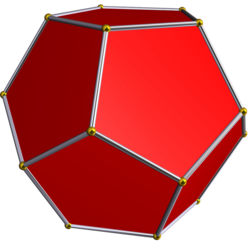
五复合正四面体可以视为正十二面体刻面（英语：faceting）后的多面体，在正十二面体凸包中每个正四面体定位在12个顶点中的其中4个顶点。也因此，正十二面体有相同的顶点布局（英语：Vertex arrangement）。^[8]

实体的五复合正四面体的旋转模型

五复合正四面体可以透过将正四面体置于旋转的二十面体群（英语：Icosahedral symmetry） (I)构造

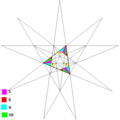
其也可以利用20组3个凹五边形组合起来构造，如上图。这种凹五边形有三种边长，其中有两组等长边，较长的等长边长度为黄金比例倒数的根号2倍，为${\displaystyle {\sqrt {3-{\sqrt {5}}}}}$，较短的等长边长度为黄金比例平方的倒数，为${\displaystyle {\frac {3-{\sqrt {5}}}{2}}}$，另外一边长度为黄金比例平方倒数的根号2倍，${\displaystyle {\sqrt {7-3{\sqrt {5}}}}}$。这种方法由温尼尔提出^[10]。

这种形状也正是每个正四面体露出来的部分。

球面镶嵌

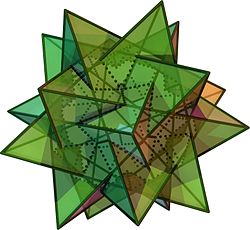透明的模型 (旋转模型)

五个互交叉的四面体

顶点坐标

由于五复合正四面体可以看作是在正十二面体中嵌入正四面体，因此其顶点坐标与正十二面体相同：

(±1, ±1, ±1)、

(0, ±1/ϕ, ±ϕ)、

(±1/ϕ, ±ϕ, 0)、

(±ϕ, 0, ±1/ϕ)。

其中ϕ = 1 + √5/2为黄金比例。

作为星形多面体

五复合正四面体是一种星形二十面体，其星状核为正二十面体、凸包为正十二面体，在杜·瓦尔记号（英语：Patrick du Val）中以Ef₁d表示。

星状图（英语：Stellation diagram）	星形	星状核	凸包
		正二十面体	正十二面体

其他的五复合正四面体

• 
  琳弦缔吉（Linkshändige）的版本
• 
  雷克弦缔吉（Rechtshändige）的版本

相关多面体

五复合正四面体与其手性镜像可组合出十复合正四面体，也就是说十复合正四面体可以看作是两个五复合正四面体的复合体^[11]。

参见

• 正四面体
• 十复合正四面体