热门问题
时间线
聊天
视角
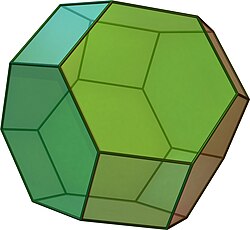
截角八面体
来自维基百科,自由的百科全书
Remove ads
在几何学中,截角八面体[1]是一种具有十四个面的半正多面体,属于阿基米德立体也是个平行多面体。由6个正方形和8个正六边形组成,共有14个面、36个边以及24个顶点[2]。因为每个面皆具点对称性质,因此截角八面体也是一种环带多面体。同时,因为它具有正方形和六边形面,因此也是一种戈德堡多面体,其戈德堡符号为GIV(1,1)。另外,由于截角八面体也是一种排列多面体[3][4],因此可以独立填满整个三维空间[5],而由截角八面体堆成的图形称为截角八面体堆砌[6]。
Remove ads
性质
截角八面体仅具有点可递性质,也就是截角八面体每一个顶点相邻面的组成都是一样的,都是一个四边形和两个六边形的公共顶点。但截角八面体不具面可递和边可递性质,因为截角八面体有两种面,四边形和六边形,边也不可递,因为截角八面体并不是所有组成边的相邻面都只有一种,截角八面体共有两种棱,一种为六边形与六边形的公共棱、另一种为六边形与四边形的公共棱。
由于截角八面体仅具有点可递性质,因此只能算是均匀多面体[7]中的半正多面体,不具拟正多面体性质。但这个多面体是阿几米德研究的13种半正多面体之一,因此截角八面体也是一种阿基米德立体[8]。

|
|
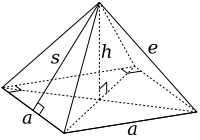
截角八面体可以从边长3a的正八面体切去六个底边长为a的四角锥构成。这些被切下来的棱锥体的底与侧面边长皆等长,因此其侧面皆为正三角形,底边长为a、底面积为a2,这些四角锥是正四角锥,是第一种詹森多面体,J1。
这些被截下来的正四角锥其高h与斜高s为:
Remove ads

|

|
| 在(±2,±2,±2)范围内的平行投影 | 每个六边形面切割成六个正三角形产生了八个新的顶点,他们分别为(±1,±1,±1)的所有组合。 |
截角立方体的体积,表面积,其中是该截半立方体的边长[2]。
- 表面积 = ≈
- 体积 = ≈
Remove ads
作法
正交投影
球面镶嵌
分割
截角八面体可分割成正中央一个正八面体、其余每个面切成8三角帐塔,剩余的部分在分割成6个正四角锥。[10]
排列多面体
截角八面体是一种排列多面体[3][4],可以以更“对称”的形式表示:四维空间中,(1,2,3,4)所有排列的坐标在三维子空间组成截角八面体。(对应的二维形状是正六边形:三维空间中,(1,2,3)所有排列的坐标在二维子空间组成正六边形。)
相关多面体及镶嵌
Remove ads

截角八面体可以独立填满整个三维空间,而这种由截角八面体堆砌出来的几何图形称为截角八面体堆砌。
截角八面体堆砌是三维空间内28个半正密铺之一,由截角八面体独立堆积而成,虽然他每个胞都全等、每边皆等长,但其不能称为正密铺,因为虽然她只由一种胞,截角八面体组成,但是该胞不是正多面体,因此并非所有“面”皆全等,因此截角八面体堆砌只能称为半正堆砌。
- 其他堆砌
 
|
 
|
 
|
 
|
 
|
 
|
... |
| 过截角立方体 | 过截角超立方体 | 过截角五维超立方体 | 过截角六维超立方体 | 过截角七维超立方体 | 过截角八维超立方体 | |
参见
参考文献
外部链接
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads