标准模型的数学表述

关于对此机制较不数学性的描述及综论，请见“标准模型”。

这篇文章讲的是粒子物理的标准模型的数学表述，而标准模型是一个包含SU(3) × SU(2) × U(1)这个由酉群的直积构成的群的内禀对称性的规范量子场论。学界常将这理论给视为对轻子、夸克、规范玻色子及希格斯玻色子等基本粒子的描述。

粒子物理的标准模型。这张图呈现了标准模型的基本粒子（希格斯玻色子、三代的夸克与轻子，以及规范玻色子等），其中包括了其名称、质量、自旋、电荷、手征性，以及其透过强交互作用、弱相互作用或电磁作用等与彼此交互作用。这张图同时显示了希格斯玻色子在电弱对称性破缺上扮演的关键角色，也显示了多种粒子的性质在（高能）对称相（图上方）及（低能）对称破缺相（图下方）之间的不同。

标准模型可重整化，且是数学自洽的^[1]；然而，尽管有着巨大且持续的成功，但依旧有些现象，无法以标准模型解释。^[2]特别地，尽管这模型涉及了狭义相对论，但这模型不涉及广义相对论；此外，一般认为标准模型会在引力子预期出现的能量或距离范畴上失效。因此在当代场论的语境中，一般将这理论视为有效场论。

量子场论

主条目：量子场论

所有已知的基本粒子的弱同位旋T₃、弱超荷Y_W及色荷。此图以弱混合角进行旋转以显示大略沿着垂直线的电荷Q。中性希格斯场（灰方块）打破电弱对称并与其他基本粒子互动，借此赋予其他粒子质量。

标准模型是种量子场论，也就是说其基本对象是对定义于时空的每一点上的量子场。量子场论将粒子视为其基底量子场的激发态（也就所谓的“量子”），而这量子场比粒子更加基本。

以下是几种标准模型牵涉到的量子场：

• 费米场ψ，也就是物质粒子所属的量子场；
• 电弱玻色场${\displaystyle W_{1},W_{2},W_{3}}$及B；
• 胶子场G_a；以及
• 希格斯场φ

这些场是量子场而非古典场的事实，表示说这些场的“值”在数学上是以算符表示的；特别地，这些场的“值”不服从交换律。作为算符，这些数值是在量子态（以右矢表记）上作用的。

场的另类表示

量子论常见的一点是，观察事物可有多个角度。第一眼看上去，以上给出的量子场可能不像上述的“基本粒子”表；然而对粒子，存在有多种不同的描述，而这些描述可能更适合某些给定的情境。

费米场

费米场ψ可以不只有一个，研究者也可对每种粒子都各别分出费米场不同的成分。这反映了量子场论的历史演变，而这是因为费米场的电子成分ψ_e（用以描述电子及其反粒子正子）是用于量子电动力学的原始ψ之故，而之后随着物理学的发展，其中又加入了ψ_μ跟ψ_τ这两个分别对应μ子跟τ子及其反粒子的场。之后的电弱理论又给费米场加入了与三个世代的中微子分别对应的${\displaystyle \psi _{\nu _{\mathrm {e} }},\psi _{\nu _{\mu }}}$及${\displaystyle \psi _{\nu _{\tau }}}$等成分。

夸克的存在给给费米场加入了更多的成分，由于要跟电子跟其他轻子一样，保持4-旋量之故，因此对于夸克每个风味跟色荷的组合，都必须有一个相对应的夸克场，而这表示费米场会有24种划分（3个带电轻子各一种、三个世代的中微子各一种，夸克则有${\displaystyle 2\times 3\times 3=18}$种，而这是因为夸克有三种风味、每种风味各两种夸克，且每种夸克各有三个不同颜色的版本之故）；此外，由于每个上述的划分都是有四个成分的双旋量（英语：bispinor）之故，因此费米场总共有96个复数值成分。

一个重要的定义是附标（英语：Dirac adjoint）费米场${\displaystyle {\bar {\psi }}}$，其定义是${\displaystyle \psi ^{\dagger }\gamma ^{0}}$，其中${\displaystyle \dagger }$是ψ的埃尔米特伴随，而γ⁰是第零个γ矩阵。若ψ是一个n × 1矩阵，那么${\displaystyle {\bar {\psi }}}$就应该要是一个1 × n矩阵。

手征性理论

ψ的一种独立分解，是按照手征性将之分拆：

• “左”手性：${\displaystyle \psi ^{\rm {L}}={\frac {1}{2}}(1-\gamma _{5})\psi }$
• “右”手性：${\displaystyle \psi ^{\rm {R}}={\frac {1}{2}}(1+\gamma _{5})\psi }$

其中${\displaystyle \gamma _{5}}$是第五个γ矩阵。这点在标准模型中非常重要，而这是因为左手性跟右手性粒子在规范场作用下有不同的表现之故。特别地，在弱同位旋的SU(2)变换下，左手性粒子呈现弱同位旋双重态，而右手性粒子则呈现单重态，也就是说，ψ_R的弱同位旋为零。举个例子，弱交互作用可将左手性电子旋转成左手性中微子（这过程会放出W⁻粒子），但不能对相对应的右手性粒子做同样的变换。另外，本来标准模型中是不包含右手性中微子的；然而，中微子振荡的发现，显示说中微子必然有质量，而由于手征性在具有质量的粒子传播的过程中可以改变之故，因此右手性中微子必然得存在；然而这不会改变弱交互作用经实验证明的手征性本质。

除此之外，U(1)对${\displaystyle \psi _{\mathrm {e} }^{\rm {L}}}$及${\displaystyle \psi _{\mathrm {e} }^{\rm {R}}}$作用方式不同，而这是因为它们有不同的弱超荷之故。

质量与交互本征态

有鉴于此，因此可做出像是中微子的质量与交互本征态之间的区别。前者是在自由空间中传播的状态；而后者则是参与互动的“不同”状态。那么哪个才是“基本”粒子？就中微子而言，一般都以其本征态来定义其“风味”（
ν
e 、
ν
μ 或
ν
τ ）；而对夸克而言，一般都以质量态来定义其风味（上、下、奇、粲、底、顶等等）。我们可借由对夸克的卡比博-小林-益川矩阵（CKM矩阵）以及对中微子的庞蒂科夫-牧-中川-坂田矩阵（PMNS矩阵）等来转换这些状态。另一方面，带荷的轻子，其质量及风味皆为其本征态。

另外，若这些矩阵存在复数项的话，就会导致直接的CP破坏，而这可解释为何在我们现在的宇宙中，物质会多于反物质。这点已在卡比博-小林-益川矩阵上得证，且预计会在庞蒂科夫-牧-中川-坂田矩阵上出现。

正负能量

最后，量子场可分解成“正能量”与“负能量”两个成分：ψ = ψ⁺ + ψ⁻。这种作法在已经建立的量子场论上不常见，但在建立量子场论的过程中，这常常是显著的特性。

玻色子

温伯格角θ_W及其与耦合常数${\displaystyle g,g'}$及${\displaystyle e}$之间的关系。此图取自T D Lee于1981年出版的《粒子物理学及场论介绍》（Particle Physics and Introduction to Field Theory）一书。

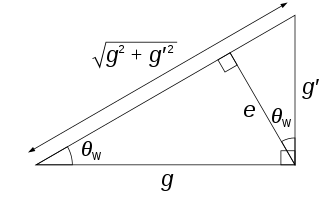
由于希格斯机制之故，电弱玻色场${\displaystyle W_{1},W_{2},W_{3}}$及${\displaystyle B}$发生混合，进而产生物理上可观察的状态。若要保持规范场不变性，这些量子场必须是无质量的；然而可观测的状态在这过程中可以“得到质量”。这些状态如下：

• 带质量中性Z玻色子：

  $${\displaystyle Z=\cos \theta _{\rm {W}}W_{3}-\sin \theta _{\rm {W}}B}$$

• 无质量中性玻色子：

  $${\displaystyle A=\sin \theta _{\rm {W}}W_{3}+\cos \theta _{\rm {W}}B}$$

• 带质量中性W玻色子：

  $${\displaystyle W^{\pm }={\frac {1}{\sqrt {2}}}\left(W_{1}\mp iW_{2}\right)}$$

其中θ_W是温伯格角。

量子场A是光子的量子场，其对应至众所皆知的电磁四维势，也就是电场与磁场。量子场Z（Z玻色子的量子场）实际上参与所有光子参与的过程，但有鉴于其庞大的质量之故，其参与一般可忽略。

微扰量子场论及互动绘景

许多以“粒子”和“力”等词语对标准模型的质性描述，都来自对此模型的微扰量子场论视角。在其中，拉格朗日量可分解为“自由场”跟“交互场”拉格朗日量，并以${\displaystyle {\mathcal {L}}={\mathcal {L}}_{0}+{\mathcal {L}}_{\mathrm {I} }}$表示。自由场表示的是孤立粒子；而交互场表示的是起自交互作用的数个粒子。这表示背后的想法是状态向量应该只在产生交互作用时改变，也就是说自由粒子是量子态保持不变者。这与量子力学的相互作用绘景相对应。

在较常见的薛定谔绘景中，即使是自由粒子，也会随时间改变：其相改变的速率取决于其能量；而在与之相对的海森堡绘景中，状态向量保持不变，而这么做的代价就是其算符（尤其可观测的）是取决于时间的。相互作用绘景则是两者的折衷，其中部分取决于时间的成分置于算符（也就是量子场）上，而其他的一些则置于状态向量上。在微扰量子场论中，前者又称为“自由场部分”，而后者称为“交互场部分”。自由场模型可得到精准解，而整个模型的解可以自由场解的微扰表示，而微扰可使用诸如戴森级数（英语：Dyson series）等方式表示。

应当注意的是，将量子场给分解为自由场及交互场的作法，在原则上是任意的。像例如说量子电动力学的重整化修改了自由场电子的质量以使之合乎物理的电子（带有电磁场），并因此给其自由场拉格朗日量加入了一个必须在交互场拉格朗日量当中以相反项抵销的项，这使其在费曼图中以带有两条线的顶点表示。这也被认为是希格斯场赋予粒子质量的方式：希格斯场中，与非零真空期望值相对应的交互项部分，被从交互场拉格朗日量移动到自由场拉格朗日量当中，在其中，这项看起来就像与希格斯场无关的质量项。

参见：费曼图

自由场

在常规的、适用于低能情境的自由场/交互场分解下，自由场遵循以下等式：

• 费米场ψ满足狄拉克方程，也就是对于每种费米子${\displaystyle f}$而言，有${\displaystyle (i\hbar \gamma ^{\mu }\partial _{\mu }-m_{\rm {f}}c)\psi _{\rm {f}}=0}$。
• 光子场A满足波动方程${\displaystyle \partial _{\mu }\partial ^{\mu }A^{\nu }=0}$。
• 希格斯场φ满足克莱因-戈尔登方程。
• 弱交互作用场Z, W^±满足Proca方程。

这些方程可得精确解。一般会首先考虑沿着每个空间轴且带有周期L的周期解，之后取其极限L → ∞可解除周期性的限制。

在周期性的状况下，任意量子场F（F可以是上述的任意量子场）的解都可以形式如下的傅立叶级数表示： $${\displaystyle F(x)=\beta \sum _{\mathbf {p} }\sum _{r}E_{\mathbf {p} }^{-{\frac {1}{2}}}\left(a_{r}(\mathbf {p} )u_{r}(\mathbf {p} )e^{-{\frac {ipx}{\hbar }}}+b_{r}^{\dagger }(\mathbf {p} )v_{r}(\mathbf {p} )e^{\frac {ipx}{\hbar }}\right)}$$ 其中各参数定义如下：

• β是归一化因此；对于费米场${\displaystyle \psi _{\rm {f}}}$其值为${\textstyle {\sqrt {m_{\rm {f}}c^{2}/V}}}$，其中${\displaystyle V=L^{3}}$是受考虑的基本胞体积；而对于光子场A^μ而言，此归一化因子为${\displaystyle \hbar c/{\sqrt {2V}}}$。
• p的总和是对所有与周期L相容的动量之总和，也就是所有形如${\displaystyle {\frac {2\pi \hbar }{L}}(n_{1},n_{2},n_{3})}$的向量之总和，其中${\displaystyle n_{1},n_{2},n_{3}}$皆为整数。
• r的总和是对诸如自旋的极化等该量子场所有自由度的总和；一般此总和为1至2或1至3的总和。
• E_p是量子场量子的动量p的相对论性质量，在静止质量为m时，其形式为${\textstyle ={\sqrt {m^{2}c^{4}+c^{2}\mathbf {p} ^{2}}}}$。
• a_r(p)及${\displaystyle b_{r}^{\dagger }(\mathbf {p} )}$分别是动量为p的“a粒子”和“b粒子”的创生及湮灭算符，其中“b粒子”是“a粒子”的反粒子。不同的场有不同的“a粒子”和“b粒子”；此外，对于一些量子场而言，“a粒子”和“b粒子”相同。
• u_r(p)及v_r(p)是带有量子场相关的向量或旋量的非算符。
• ${\displaystyle p=(E_{\mathbf {p} }/c,\mathbf {p} )}$是带有动量p的量子的四维动量。${\displaystyle px=p_{\mu }x^{\mu }}$则是四维向量的内积。

在取极限L → ∞的状况下，由于藏于β的参数V之故，此和会变成一个积分，而β的数值会取决于对${\displaystyle u_{r}(\mathbf {p} )}$及${\displaystyle v_{r}(\mathbf {p} )}$选取的归一。

技术上而言，${\displaystyle a_{r}^{\dagger }(\mathbf {p} )}$是右矢的算符a_r(p)在内积空间中的埃尔米特伴随。之所以将${\displaystyle a_{r}^{\dagger }(\mathbf {p} )}$以及a_r(p)给鉴别做创生及湮灭算符，是因为这是比较其中之一在其上发生作用前后保存的量的结果之故。做为例子，${\displaystyle a_{r}^{\dagger }(\mathbf {p} )}$可视做加添一个粒子，而这是因为这会给粒子数算符的特征值加1之故；而这样操作之后，粒子的动量应当要是p，这是因为以向量为值的动量算符会如此增加之故。人们一般以量子场的算符表示作为起始进行衍伸。将带有${\displaystyle \dagger }$的算符做为创生算符是一个习惯，而这是因为导入其彼此间的交换符号之故。

一个在微扰量子场论计算中重要的步骤是将上述“算符”因子a与b从其向量或旋量因子u与v中分离。费曼图顶点的设置来自源于不同因子的交互拉格朗日量u与v彼此相合的方式；而其边的设置则来自a与b必须移动以在正规化的形式的戴森级数中设项的方式。

交互场项及路径积分法

在不使用创生及湮灭算符（也就是“常规”形式）的状况下，也可借由路径积分得到拉格朗日量，这作法最初由费曼基于狄拉克的工作所发展。费曼图乃是交互项的图像化展示。详情可见费曼图一文说明。

拉格朗日形式

标准模型中的互动。所有模型中的费曼图都起自这些顶点的混合。q代表任何夸克、g代表胶子、X代表任何带荷粒子、γ代表光子、f代表任何费米子、m代表任何带质量粒子（中微子可能是其例外）、m_B<nowiki>代表任何带质量玻色子。在图中有多个以“∕”分隔的粒子标签的部分，其中一个标签被使用；而图中有多个以“∣”分隔的粒子标签的部分，其标签须以相同顺序选取。像例如说，在有四个玻色子的电弱作用的状况下，可行的图有WWWW、WWZZ、WWγγ、WWZγ等几种组合。每个列出的顶点的共轭（将箭头方向倒过来）也是允许的。^[3]

我们现在可以给出前述出现在标准模型中的自由与交互场的拉格朗日量。任何如此的项都必须是规范且参考系不变的，不然物理法则会取决于任意的选择或者观察者所在的参考系。因此包含平移对称（英语：translational symmetry）、旋转对称及作为狭义相对论核心的惯性座标系的全域庞加莱对称必须成立。局域SU(3) × SU(2) × U(1)规范场对称是种内部对称如下所见，在一些合适的关系定义后，规范场对称的三个因子会给出三种基本作用力。

动能项

自由粒子可以一个质量项及一个与量子场“移动”有关的“动能”项表示。

费米场

狄拉克费米子的动能项如下：

$${\displaystyle i{\bar {\psi }}\gamma ^{\mu }\partial _{\mu }\psi }$$

其中的表记跟前文一致。ψ可指任何标准模型中的狄拉克费米子；此外一般而言，如下所述，这项可包含在耦合（并因此得到一般的动态项）当中。

规范场

对于自旋为1的量子场，首先定义场强度张量：

$${\displaystyle F_{\mu \nu }^{a}=\partial _{\mu }A_{\nu }^{a}-\partial _{\nu }A_{\mu }^{a}+gf^{abc}A_{\mu }^{b}A_{\nu }^{c}}$$

对于给定的、耦合常数为g的规范场（此处以A表记）而言， f ^abc这个量是该规范群的结构常数，而这常数可由以下交换子定义：

$${\displaystyle [t_{a},t_{b}]=if^{abc}t_{c},}$$

其中t_i是这个群的生成元。在交换群（如此处用的U(1)）中，结构常数会消失，而这是因为生成元t_a全都满足交换律之故。当然，这非一般情况，而这是因为标准模型也包含了非交换的SU(2)及SU(3)群之故。而这些非交换群也是杨-米尔斯规范场论出现的原因。

我们需要引入三个与SU(3) × SU(2) × U(1)这个群的每个子群相对应的规范场：

• 胶子场张量会以${\displaystyle G_{\mu \nu }^{a}}$表示，其中a这指数表示了代表SU(3)出现的八种色态的元素。强耦合常数一般会以g_s（或在不引起混淆的状况下记做g）表示。导致标准模型这部分发现的观察可见量子色动力学一文。
• SU(2)的规范场张量会以${\displaystyle W_{\mu \nu }^{a}}$表示，其中a表示了此群中出现的三个世代。其耦合常数一般会以g_w（或在不引起混淆的状况下记做g）表示。而其规范场会以${\displaystyle W_{\mu }^{a}}$表示。
• U(1)的规范场张量会以B_μν表示，其中g′表示其耦合，而其规范场会以B_μ表示。

因此动能项可表示如下：

$${\displaystyle {\mathcal {L}}_{\rm {kin}}=-{1 \over 4}B_{\mu \nu }B^{\mu \nu }-{1 \over 2}\mathrm {tr} W_{\mu \nu }W^{\mu \nu }-{1 \over 2}\mathrm {tr} G_{\mu \nu }G^{\mu \nu }}$$

其迹位于分别隐藏于SU(2)及SU(3)的指数中的W及G之上。而这些双指数物件乃是衍生自向量场W及G的场强度；此外，还有两个隐藏参数：SU(2)及SU(3)的角度。

耦合项

下一步是将规范场与费米场“耦合”以描述交互作用。

电弱部分

主条目：电弱交互作用

电弱交互作用可以对称群U(1) × SU(2)_L表示，其中L表示说其只与左手性费米子耦合。

$${\displaystyle {\mathcal {L}}_{\mathrm {EW} }=\sum _{\psi }{\bar {\psi }}\gamma ^{\mu }\left(i\partial _{\mu }-g^{\prime }{1 \over 2}Y_{\mathrm {W} }B_{\mu }-g{1 \over 2}{\boldsymbol {\tau }}\mathbf {W} _{\mu }\right)\psi }$$

其中B_μ是U(1)规范场；Y_W是弱超荷，也是U(1)的生成元；W_μ是有三个部分的SU(2)规范场；而τ由泡利矩阵（也是SU(2)群的极小生成元）组成，且其特征值给出弱同位旋。应当注意的是，我们给弱超荷定义了一个新的、不同于量子电动力学的新U(1)群，而这么做是为了统一弱作用力。

作为弱同位旋第三成分T₃（又作T_z, I₃或I_z等）的电荷Q及弱超荷Y_W之间，有以下关系： $${\displaystyle Q=T_{3}+{\tfrac {1}{2}}Y_{\rm {W}},}$$ （或用“另外的”常规表示，有Q = T₃ + Y_W） 用于此篇文的第一个常规表示与盖尔曼-西岛关系等价，这使得超荷等于同位多重态平均荷的两倍。

我们可接着定义弱同位旋的保守流（英语：conserved current）如下： $${\displaystyle \mathbf {j} _{\mu }={1 \over 2}{\bar {\psi }}_{\rm {L}}\gamma _{\mu }{\boldsymbol {\tau }}\psi _{\rm {L}}}$$ 并定义弱超荷的保守流如下： $${\displaystyle j_{\mu }^{Y}=2(j_{\mu }^{\rm {em}}-j_{\mu }^{3})~,}$$ 其中${\displaystyle j_{\mu }^{\rm {em}}}$是电流，而${\displaystyle j_{\mu }^{3}}$是第三弱同位旋流。如上所言，这些粒子流彼此混合以产生物理上观测到的玻色子，这也导致了耦合常数间可测试的关系。

换个方式解释，我们可以借由将不同项目从拉格朗日形式取出的做法来观察电弱交互作用的效应。我们可看见SU(2)对称在每个包含于ψ的（左手性）费米子二重态上发生作用，像例如说 $${\displaystyle -{g \over 2}({\bar {\nu }}_{e}\;{\bar {e}})\tau ^{+}\gamma _{\mu }(W^{+})^{\mu }{\begin{pmatrix}{\nu _{e}}\\e\end{pmatrix}}=-{g \over 2}{\bar {\nu }}_{e}\gamma _{\mu }(W^{+})^{\mu }e}$$ 其中粒子都被理解为左手性的，且其中 $${\displaystyle \tau ^{+}\equiv {1 \over 2}(\tau ^{1}{+}i\tau ^{2})={\begin{pmatrix}0&1\\0&0\end{pmatrix}}}$$

这是一个对应到“弱同位旋空间的旋转”或e_L与ν_eL之间，透过发射W⁻玻色子进行的变换。

另一方面，U(1)对称与电磁作用力类似，但经由中性的Z⁰，作用于所有带有弱超荷的（左手性跟右手性的）费米子上，也透过光子作用在带有电荷的费米子上。

量子色动力学部分

主条目：量子色动力学

量子色动力学部分定义了夸克与胶子之间的交互作用，而这部分带有由T_a生成的SU(3)对称。

由于轻子不与胶子作用之故，因此轻子与此部分无涉。夸克与胶子场耦合的狄拉克拉格朗日量如下：

$${\displaystyle {\mathcal {L}}_{\mathrm {QCD} }=i{\overline {U}}\left(\partial _{\mu }-ig_{s}G_{\mu }^{a}T^{a}\right)\gamma ^{\mu }U+i{\overline {D}}\left(\partial _{\mu }-ig_{s}G_{\mu }^{a}T^{a}\right)\gamma ^{\mu }D.}$$

其中U与D是分别与上类与下类夸克相关的狄拉克旋量，而其他的表记则同前文。

质量项与希格斯机制

质量项

对于任意费米子ψ而言，起自狄拉克拉格朗日量的质量项是${\displaystyle -m{\bar {\psi }}\psi }$，这项在电弱交互作用下并非不变的。这点可从将ψ给写作左手与右手部分的总和看出（此处跳过实际计算）：

$${\displaystyle -m{\bar {\psi }}\psi =-m({\bar {\psi }}_{\rm {L}}\psi _{\rm {R}}+{\bar {\psi }}_{\rm {R}}\psi _{\rm {L}})}$$

其中${\displaystyle {\bar {\psi }}_{\rm {L}}\psi _{\rm {L}}}$及${\displaystyle {\bar {\psi }}_{\rm {R}}\psi _{\rm {R}}}$项给出的贡献并未出现。

我们从中可见说质量生成作用是借由不断翻转粒子的手性而发生的。

半自旋粒子不带有同于SU(2)表示、并具有相同或相反弱超荷的左右手对，因此在假定这些规范荷在真空中不变的状况下，没有任何半自旋粒子可翻转手性，也因此必须保持无质量；此外，我们从实验中可知W和Z玻色子带质量，但玻色子质量项包含了A^μA_μ等组合，而这些组合明确地取决于规范的选取。因此没有任何标准模型中的费米子或玻色子可以“在开始时”就有质量，而其质量必须透过其他机制取得。

希格斯机制

主条目：希格斯机制

解决这些问题的方法来自希格斯机制，其中涉及了被“吸收”入带质量玻色子、成为其自由度一部分（此处尽量简短解释），以及透过汤川耦合以生成看起来是质量项的标量场，而标量场的值，取决于希格斯机制的实际形式。

在标准模型中，希格斯场是一个SU(2)_L群的复标量场：

$${\displaystyle \phi ={\frac {1}{\sqrt {2}}}{\begin{pmatrix}\phi ^{+}\\\phi ^{0}\end{pmatrix}},}$$

其中上标的+和0表示其成分的电荷Q。两成分的弱超荷Y_W都是1。

希格斯部分的拉格朗日量如下：

$${\displaystyle {\mathcal {L}}_{\rm {H}}=\left[\left(\partial _{\mu }-igW_{\mu }^{a}t^{a}-ig'Y_{\phi }B_{\mu }\right)\phi \right]^{2}+\mu ^{2}\phi ^{\dagger }\phi -\lambda (\phi ^{\dagger }\phi )^{2},}$$

其中λ > 0且μ² > 0以使得自发对称破缺机制可套用。在此有一个开始时隐藏于势能形态、但非常重要的参数。

统一性规范（英语：unitarity gauge）下，可设${\displaystyle \phi ^{+}=0}$并使得${\displaystyle \phi ^{0}}$为实数。在这种状况下，${\displaystyle \langle \phi ^{0}\rangle =v}$即是希格斯场不消逝的真空期望值。${\displaystyle v}$带有质量单位，且在标准模型中是唯一不是无因次的参数。

此外，其数值远小于普朗克尺度且大约是希格斯粒子质量的两倍，而这也给了标准模型中所有其他粒子的质量设置了一个尺度。这是整个模型中，唯一确实微调到微小非零数值的参数。W_μ及B_μ当中出现二次项，而这些项目赋予了W和Z玻色子质量：

$${\displaystyle {\begin{aligned}M_{\rm {W}}&={\tfrac {1}{2}}vg\\M_{\rm {Z}}&={\tfrac {1}{2}}v{\sqrt {g^{2}+{g'}^{2}}}\end{aligned}}}$$

希格斯玻色子本身的质量则为${\textstyle M_{\rm {H}}={\sqrt {2\mu ^{2}}}\equiv {\sqrt {2\lambda v^{2}}}.}$

汤川耦合

汤川耦合项如下：

$${\displaystyle {\mathcal {L}}_{\text{Yukawa}}=(Y_{u})_{mn}({\bar {q}}_{L})_{m}{\tilde {\varphi }}(u_{R})_{n}+(Y_{d})_{mn}({\bar {q}}_{L})_{m}\varphi (d_{R})_{n}+(Y_{e})_{mn}({\bar {L}}_{L})_{m}{\tilde {\varphi }}(e_{R})_{n}+\mathrm {h.c.} }$$

其中${\displaystyle Y_{u}}$、${\displaystyle Y_{d}}$及${\displaystyle Y_{e}}$为3 × 3汤川耦合矩阵，其中的mn项给出m和n这两世代的耦合，而${\displaystyle h.c.}$表示前述各项的埃尔米特共轭。

${\displaystyle q_{L}}$及${\displaystyle L_{L}}$等量子场代表左手性夸克与轻子的二重态；类似地，${\displaystyle u_{R},d_{R}}$及${\displaystyle e_{R}}$等量子场代表右手性上类夸克、下类夸克与轻子的单重态。最后，${\displaystyle \varphi }$表示希格斯双重态，且有${\displaystyle {\tilde {\varphi }}=i\tau _{2}\varphi ^{*}}$

中微子质量

如前所述，证据显示中微子有质量；然而在标准模型中，右手性中微子并不存在，因此即使是汤川耦合中微子，也依旧是无质量的。

对此一个明显的解^[4]是“加入右手性中微子”ν_R，而这样座要求在汤川耦合的部分中加入新的“狄拉克质量”项：

$${\displaystyle {\mathcal {L}}_{\nu }^{\text{Dir}}=(Y_{\nu })_{mn}({\bar {L}}_{L})_{m}\varphi (\nu _{R})_{n}+\mathrm {h.c.} }$$

但这样的量子场必须是惰性中微子，而这是因为在实验上，右手性粒子皆属于同位旋单重态（T₃ = 0）且其电荷Q = 0, implying Y_W = 0之故，此点可见上说明。也就是说，这样的粒子甚至不参与弱交互作用。目前惰性中微子的实验证据尚不明确。^[5]

另一个可能性是假定中微子满足马约拉纳方程式，而因为中微子的电荷为零之故，因此这乍看之下是可能的。在这种状况下，一个新的“马约拉纳质量”项会加入汤川耦合的部分中：

$${\displaystyle {\mathcal {L}}_{\nu }^{\text{Maj}}=-{\frac {1}{2}}m\left({\overline {\nu }}^{C}\nu +{\overline {\nu }}\nu ^{C}\right)}$$

其中C指的是共轭粒子（也就是反粒子），而${\displaystyle \nu }$这项则一致地为左手性（或右手性）。应当注意的一个反粒子的左手性投射是个右手性量子场；由于有些人会用不同的表记之故，因此这里要保持注意。

在此，我们基本翻转了左手性中微子和右手性反中微子，中微子可能是（但不必然）自身的反粒子，但这非必然的，因此这些粒子是相同的；然而，对于左手性中微子而言，这项会改变弱超荷达两单位，而这在标准希格斯交互作用下是不可能的，因此这要求将希格斯场延伸以包含额外带弱超荷为2的三重态；^[4]而对于右手性中微子而言，没有任何对希格斯场的延伸是必要的。不管在左手性或右手性的状况下，马约纳拉项违反轻子数守恒，但这可能性可能位于既有实验对这类违背的侦测敏感度的范围之外。

将狄拉克与马约拉纳质量项同时包含在同一个理论中是可能的，而这可借由将右手性中微子连结到物理上尚未清楚的大统一尺度^[6]，为中微子质量观测到的微小的大小提供一个“自然的”（相对于仅包含狄拉克质量项的作法）解释。详情可见翘翘板机制一文。

由于在上述任何情况下，新的量子场都必须引入以解释实验结果之故，因此中微子可作为超越标准模型的物理学明显的开端。

详细讯息

本段落为模型的一些面相提供更多细节，并提供一些参考资料。明确表达的拉格朗日项也可见于电弱交互作用一文。

量子场内容的详细讯息

标准模型有如下的场，这些场描述一个世代的轻子与夸克，而目前已知这些粒子有三个世代，因此对每种费米场都有三个复本。由CPT对称性可知，每种费米子都有与之相对的、带有相反宇称和电荷的反费米子。若一个左手性费米子存在于某些表示上，那其反粒子（右手性反费米子）也会存在于相对应的对偶表示（英语：dual representation）上。^[7]（当注意的是由于SU(2)是伪实数（英语：pseudo-real）之故，因此有${\displaystyle {\bar {\mathbf {2} }}={\mathbf {2} }}$）“表示”这直列指称说每个场在何种规范群的表示下进行转换，转换当中的顺序分别为对${\displaystyle (SU(3),SU(2),U(1))}$的转换，而对于${\displaystyle U(1)}$群也会给出弱超荷的值，在轻子场部分中，这数值的左手场部分两倍于右手场部分；但在夸克部分中，这数值的左手场部分与右手场部分相等。

标准模型的量子场内容
自旋为1的规范场
符号	相关的荷	群	耦合	表示[8]
${\displaystyle B}$	弱超荷	U(1)Y	${\displaystyle g'}$ or ${\displaystyle g_{1}}$	${\displaystyle (\mathbf {1} ,\mathbf {1} ,0)}$
${\displaystyle W}$	弱同位旋	SU(2)L	${\displaystyle g_{w}}$ or ${\displaystyle g_{2}}$	${\displaystyle (\mathbf {1} ,\mathbf {3} ,0)}$
${\displaystyle G}$	色荷	SU(3)C	${\displaystyle g_{s}}$ or ${\displaystyle g_{3}}$	${\displaystyle (\mathbf {8} ,\mathbf {1} ,0)}$
自旋为1⁄2的费米子
符号	名称	重子数	轻子数	表示
${\displaystyle q_{\rm {L}}}$	左手夸克	${\displaystyle \textstyle {\frac {1}{3}}}$	${\displaystyle 0}$	${\displaystyle (\mathbf {3} ,\mathbf {2} ,\textstyle {\frac {1}{3}})}$
${\displaystyle u_{\rm {R}}}$	右手夸克（上类）	${\displaystyle \textstyle {\frac {1}{3}}}$	${\displaystyle 0}$	${\displaystyle ({\mathbf {3} },\mathbf {1} ,\textstyle {\frac {4}{3}})}$
${\displaystyle d_{\rm {R}}}$	右手夸克（下类）	${\displaystyle \textstyle {\frac {1}{3}}}$	${\displaystyle 0}$	${\displaystyle ({\mathbf {3} },\mathbf {1} ,-\textstyle {\frac {2}{3}})}$
${\displaystyle \ell _{\rm {L}}}$	左手轻子	${\displaystyle 0}$	${\displaystyle 1}$	${\displaystyle (\mathbf {1} ,\mathbf {2} ,-1)}$
${\displaystyle \ell _{\rm {R}}}$	右手轻子	${\displaystyle 0}$	${\displaystyle 1}$	${\displaystyle (\mathbf {1} ,\mathbf {1} ,-2)}$
自旋为0的标量玻色子
符号	名称	表示
${\displaystyle H}$	希格斯玻色子	${\displaystyle (\mathbf {1} ,\mathbf {2} ,1)}$