泽尔尼克多项式

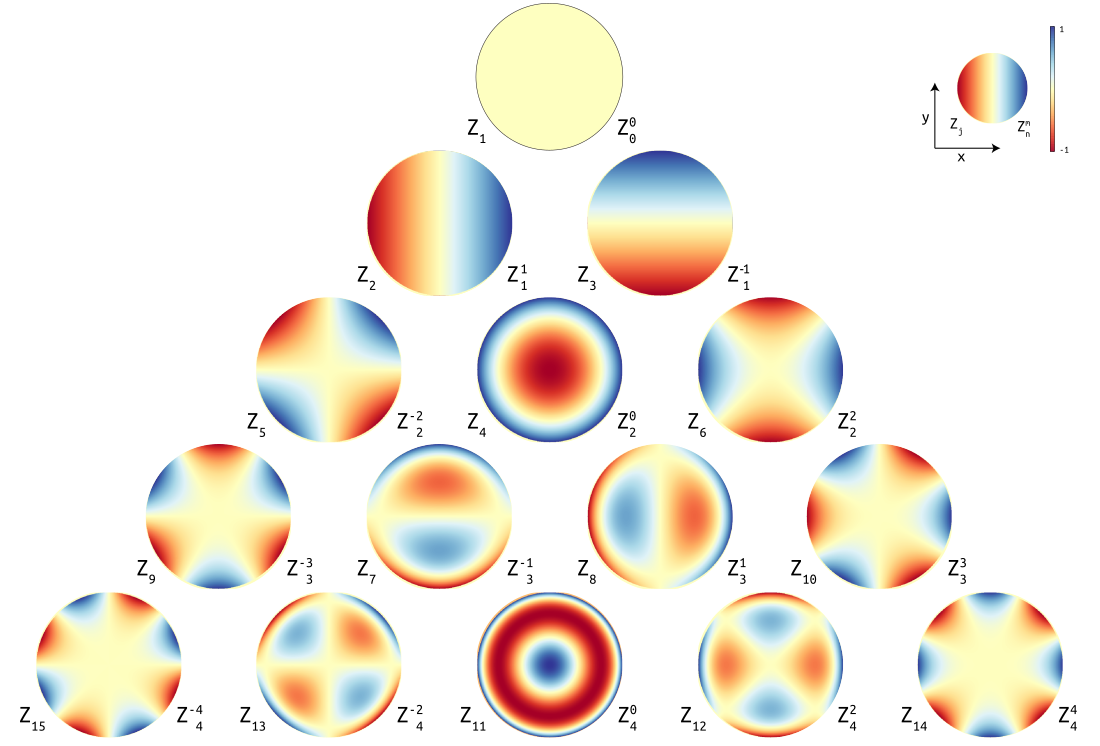
泽尔尼克多项式是一个以1953年获诺贝尔物理学奖荷兰物理学家弗里茨·泽尔尼克命名的正交多项式，分为奇、偶两类

头15个泽尔尼克多项式

20个泽尔尼克多项式 以Noll序列表示

奇多项式：

${\displaystyle Z_{n}^{m}(\rho ,\varphi )=R_{n}^{m}(\rho )\,\cos(m\,\varphi )\!}$

偶多项式

${\displaystyle Z_{n}^{-m}(\rho ,\varphi )=R_{n}^{m}(\rho )\,\sin(m\,\varphi ),\!}$

其中${\displaystyle n\geq m}$ 为非负整数，

${\displaystyle \phi }$为方位角

${\displaystyle 0\leq \rho \leq 1}$ 为径向距离

如果 n-m为偶数则

${\displaystyle R_{n}^{m}(\rho )=\sum _{k=0}^{\tfrac {n-m}{2}}{\frac {(-1)^{k}\,(n-k)!}{k!\left({\tfrac {n+m}{2}}-k\right)!\left({\tfrac {n-m}{2}}-k\right)!}}\;\rho ^{n-2\,k}}$

如果n-m为奇数，则

${\displaystyle R_{n}^{m}(\rho )=0}$

泽尔尼克多项式的超几何函数表示

泽尔尼克多项式也可以表示为超几何函数

${\displaystyle {\begin{aligned}R_{n}^{m}(\rho )&={\binom {n}{\tfrac {n+m}{2}}}\rho ^{n}\ {}_{2}F_{1}\left(-{\tfrac {n+m}{2}},-{\tfrac {n-m}{2}};-n;\rho ^{-2}\right)\\&=(-1)^{\tfrac {n+m}{2}}{\binom {\tfrac {n+m}{2}}{\tfrac {n-m}{2}}}\rho ^{m}\ {}_{2}F_{1}\left(1+n,1-{\tfrac {n-m}{2}};1+{\tfrac {n+m}{2}};\rho ^{2}\right)\end{aligned}}}$

Noll 序列

Noll 用一个J数字表示 [n,m]:如下表

n,m	0,0	1,1	1,−1	2,0	2,−2	2,2	3,−1	3,1	3,−3	3,3
j	1	2	3	4	5	6	7	8	9	10
n,m	4,0	4,2	4,−2	4,4	4,−4	5,1	5,−1	5,3	5,−3	5,5
j	11	12	13	14	15	16	17	18	19	20

泽尔尼克多项式

由于

${\displaystyle I_{j}=\int _{0}^{2\pi }\int _{0}^{1}Z_{j}^{2}\,\rho \,d\rho \,d\theta =k_{j}*\pi .}$

其中${\displaystyle k_{j}}$因j而异，

${\displaystyle k_{1}=1}$

${\displaystyle k_{2}={\frac {1}{4}}}$

${\displaystyle k_{3}={\frac {1}{4}}}$

${\displaystyle k_{4}={\frac {1}{3}}}$

${\displaystyle k_{5}={\frac {1}{6}}}$

必须先归一化

令${\displaystyle Z_{j}=Z_{j}/{\sqrt {(}}k_{j})}$

使得

${\displaystyle I_{j}=\int _{0}^{2\pi }\int _{0}^{1}Z_{j}^{2}\,\rho \,d\rho \,d\theta =\pi .}$

归一化泽尔尼克多项式以Noll序列排列如下：

Noll index (${\displaystyle j}$)	Radial degree (${\displaystyle n}$)	Azimuthal degree (${\displaystyle m}$)	${\displaystyle Z_{j}}$	Classical name
1	0	0	${\displaystyle 1}$	Piston
2	1	1	${\displaystyle 2\rho \cos \theta }$	Tip (lateral position) (X-Tilt)
3	1	−1	${\displaystyle 2\rho \sin \theta }$	Tilt (lateral position) (Y-Tilt)
4	2	0	${\displaystyle {\sqrt {3}}(2\rho ^{2}-1)}$	Defocus (longitudinal position)
5	2	−2	${\displaystyle {\sqrt {6}}\rho ^{2}\sin 2\theta }$	Astigmatism
6	2	2	${\displaystyle {\sqrt {6}}\rho ^{2}\cos 2\theta }$	Astigmatism
7	3	−1	${\displaystyle {\sqrt {8}}(3\rho ^{3}-2\rho )\sin \theta }$	Coma
8	3	1	${\displaystyle {\sqrt {8}}(3\rho ^{3}-2\rho )\cos \theta }$	Coma
9	3	−3	${\displaystyle {\sqrt {8}}\rho ^{3}\sin 3\theta }$	Trefoil
10	3	3	${\displaystyle {\sqrt {8}}\rho ^{3}\cos 3\theta }$	Trefoil
11	4	0	${\displaystyle {\sqrt {5}}(6\rho ^{4}-6\rho ^{2}+1)}$	Third-order spherical
12	4	2	${\displaystyle {\sqrt {10}}(4\rho ^{4}-3\rho ^{2})\cos 2\theta }$	—
13	4	−2	${\displaystyle {\sqrt {10}}(4\rho ^{4}-3\rho ^{2})\sin 2\theta }$	—
14	4	4	${\displaystyle {\sqrt {10}}\rho ^{4}\cos 4\theta }$	—
15	4	−4	${\displaystyle {\sqrt {10}}\rho ^{4}\sin 4\theta }$	—

正交性

径向正交性

${\displaystyle \int _{0}^{1}\rho {\sqrt {2n+2}}R_{n}^{m}(\rho )\,{\sqrt {2n'+2}}R_{n'}^{m}(\rho )\,d\rho =\delta _{n,n'}.}$

角度正交性

${\displaystyle \int _{0}^{2\pi }\cos(m\varphi )\cos(m'\varphi )\,d\varphi =\epsilon _{m}\pi \delta _{|m|,|m'|},}$

${\displaystyle \int _{0}^{2\pi }\sin(m\varphi )\sin(m'\varphi )\,d\varphi =(-1)^{m+m'}\pi \delta _{|m|,|m'|};\quad m\neq 0,}$

${\displaystyle \int _{0}^{2\pi }\cos(m\varphi )\sin(m'\varphi )\,d\varphi =0,}$

其中 ${\displaystyle \epsilon _{m}}$ 称为Neumann因子，其数值为 2 如果满足 ${\displaystyle m=0}$ ，数值为 1，如果 ${\displaystyle m\neq 0}$.

径向与角度正交性

${\displaystyle \int Z_{n}^{m}(\rho ,\varphi )Z_{n'}^{m'}(\rho ,\varphi )\,d^{2}r={\frac {\epsilon _{m}\pi }{2n+2}}\delta _{n,n'}\delta _{m,m'},}$

其中 ${\displaystyle d^{2}r=\rho \,d\rho \,d\varphi }$ 为 雅可比矩阵

${\displaystyle n-m}$ 与 ${\displaystyle n'-m'}$ 都是偶数.

参考文献

• 埃里克·韦斯坦因. Zernike Polynomial. MathWorld.
• Callahan, P. G.; De Graef, M. Precipitate shape fitting and reconstruction by means of 3D Zernike functions. Model. Simul. Mat. Sci. Engin. 2012, 20: 015003. Bibcode:2012MSMSE..20a5003C. doi:10.1088/0965-0393/20/1/015003.
• Campbell, C. E. Matrix method to find a new set of Zernike coefficients form an original set when the aperture radius is changed. J. Opt. Soc. Am. A. 2003, 20 (2): 209. Bibcode:2003JOSAA..20..209C. doi:10.1364/JOSAA.20.000209.
• Cerjan, C. The Zernike-Bessel representation and its application to Hankel transforms. J. Opt. Soc. Am. A. 2007, 24 (6): 1609. Bibcode:2007JOSAA..24.1609C. doi:10.1364/JOSAA.24.001609.
• Comastri, S. A.; Perez, L. I.; Perez, G. D.; Martin, G.; Bastida Cerjan, K. Zernike expansion coefficients: rescaling and decentering for different pupils and evaluation of corneal aberrations. J. Opt. Soc. Am. A. 2007, 9 (3): 209. Bibcode:2007JOptA...9..209C. doi:10.1088/1464-4258/9/3/001.
• Conforti, G. Zernike aberration coefficients from Seidel and higher-order power-series coefficients. Opt. Lett. 1983, 8 (7): 407–408. Bibcode:1983OptL....8..407C. doi:10.1364/OL.8.000407.
• Dai, G-m.; Mahajan, V. N. Zernike annular polynomials and atmospheric turbulence. J. Opt. Soc. Am. A. 2007, 24: 139 [2015-01-29]. Bibcode:2007JOSAA..24..139D. doi:10.1364/JOSAA.24.000139. （原始内容存档于2019-07-02）.
• Dai, G-m. Scaling Zernike expansion coefficients to smaller pupil sizes: a simpler formula. J. Opt. Soc. Am. A. 2006, 23 (3): 539 [2015-01-29]. Bibcode:2006JOSAA..23..539D. doi:10.1364/JOSAA.23.000539. （原始内容存档于2019-07-02）.
• Díaz, J. A.; Fernández-Dorado, J.; Pizarro, C.; Arasa, J. Zernike Coefficients for Concentric, Circular, Scaled Pupils: An Equivalent Expression. Journal of Modern Optics. 2009, 56 (1): 149–155. Bibcode:2009JMOp...56..149D. doi:10.1080/09500340802531224.
• Díaz, J. A.; Fernández-Dorado, J. Zernike Coefficients for Concentric, Circular, Scaled Pupils. [2015-01-29]. （原始内容存档于2020-03-18）. from The Wolfram Demonstrations Project.
• Farokhi, Sajad; Shamsuddin, Siti Mariyam; Flusser, Jan; Sheikh, U.U; Khansari, Mohammad; Jafari-Khouzani, Kourosh. Rotation and noise invariant near-infrared face recognition by means of Zernike moments and spectral regression discriminant analysis. Journal of Electronic Imaging. 2013, 22 (1). Bibcode:2013JEI....22a3030F. doi:10.1117/1.JEI.22.1.013030.
• Gu, J.; Shu, H. Z.; Toumoulin, C.; Luo, L. M. A novel algorithm for fast computation of Zernike moments. Pattern Recogn. 2002, 35 (12): 2905–2911. doi:10.1016/S0031-3203(01)00194-7.
• Herrmann, J. Cross coupling and aliasing in modal wave-front estimation. J. Opt. Soc. Am. 1981, 71 (8): 989 [2015-01-29]. Bibcode:1981JOSA...71..989H. doi:10.1364/JOSA.71.000989. （原始内容存档于2019-07-02）.
• Hu, P. H.; Stone, J.; Stanley, T. Application of Zernike polynomials to atmospheric propagation problems. J. Opt. Soc. Am. A. 1989, 6 (10): 1595. Bibcode:1989JOSAA...6.1595H. doi:10.1364/JOSAA.6.001595.
• Kintner, E. C. On the mathematical properties of the Zernike Polynomials. Opt. Acta. 1976, 23 (8): 679. Bibcode:1976AcOpt..23..679K. doi:10.1080/713819334.
• Lawrence, G. N.; Chow, W. W. Wave-front tomography by Zernike Polynomial decomposition. Opt. Lett. 1984, 9 (7): 267. Bibcode:1984OptL....9..267L. doi:10.1364/OL.9.000267.
• Liu, Haiguang; Morris, Richard J.; Hexemer, A.; Grandison, Scott; Zwart, Peter H. Computation of small-angle scattering profiles with three-dimensional Zernike polynomials. Acta Cryst. A. 2012, (A69): 278–285. doi:10.1107/S010876731104788X.
• Lundström, L.; Unsbo, P. Transformation of Zernike coefficients: scaled, translated and rotated wavefronts with circular and elliptical pupils. J. Opt. Soc. Am. A. 2007, 24 (3): 569. Bibcode:2007JOSAA..24..569L. doi:10.1364/JOSAA.24.000569.
• Mahajan, V. N. Zernike annular polynomials for imaging systems with annular pupils. J. Opt. Soc. Am. 1981, 71: 75. Bibcode:1981JOSA...71...75M. doi:10.1364/JOSA.71.000075.
• Mathar, R. J. Third Order Newton's Method for Zernike Polynomial Zeros. 2007. Bibcode:2007arXiv0705.1329M. arXiv:0705.1329  [math.NA]. cite arXiv模板填写了不支持的参数 (帮助)
• Mathar, R. J. Zernike Basis to Cartesian Transformations. Serbian Astronomical Journal. 2009, 179 (179): 107–120. Bibcode:2009SerAj.179..107M. arXiv:0809.2368 . doi:10.2298/SAJ0979107M.
• Prata Jr, A.; Rusch, W. V. T. Algorithm for computation of Zernike polynomials expansion coefficients. Appl. Opt. 1989, 28 (4): 749 [2015-01-29]. Bibcode:1989ApOpt..28..749P. doi:10.1364/AO.28.000749. （原始内容存档于2019-07-02）.
• Schwiegerling, J. Scaling Zernike expansion coefficients to different pupil sizes. J. Opt. Soc. Am. A. 2002, 19 (10): 1937 [2015-01-29]. Bibcode:2002JOSAA..19.1937S. doi:10.1364/JOSAA.19.001937. （原始内容存档于2019-07-02）.
• Sheppard, C. J. R.; Campbell, S.; Hirschhorn, M. D. Zernike expansion of separable functions in Cartesian coordinates. Appl. Opt. 2004, 43 (20): 3963 [2015-01-29]. Bibcode:2004ApOpt..43.3963S. doi:10.1364/AO.43.003963. （原始内容存档于2019-07-02）.
• Shu, H.; Luo, L.; Han, G.; Coatrieux, J.-L. General method to derive the relationship between two sets of Zernike coefficients corresponding to different aperture sizes. J. Opt. Soc. Am. A. 2006, 23 (8): 1960 [2015-01-29]. Bibcode:2006JOSAA..23.1960S. doi:10.1364/JOSAA.23.001960. （原始内容存档于2019-07-02）.
• Swantner, W.; Chow, W. W. Gram-Schmidt orthogonalization of Zernike polynomials for general aperture shapes. Appl. Opt. 1994, 33 (10): 1832 [2015-01-29]. Bibcode:1994ApOpt..33.1832S. doi:10.1364/AO.33.001832. （原始内容存档于2015-01-24）.
• Tango, W. J. The circle polynomials of Zernike and their application in optics. Appl. Phys. A. 1977, 13 (4): 327. Bibcode:1977ApPhy..13..327T. doi:10.1007/BF00882606.
• Tyson, R. K. Conversion of Zernike aberration coefficients to Seidel and higher-order power series aberration coefficients. Opt. Lett. 1982, 7 (6): 262. Bibcode:1982OptL....7..262T. doi:10.1364/OL.7.000262.
• Wang, J. Y.; Silva, D. E. Wave-front interpretation with Zernike Polynomials. Appl. Opt. 1980, 19 (9): 1510. Bibcode:1980ApOpt..19.1510W. doi:10.1364/AO.19.001510.
• Barakat, R. Optimum balanced wave-front aberrations for radially symmetric amplitude distributions: Generalizations of Zernike polynomials. J. Opt. Soc. Am. 1980, 70 (6): 739. Bibcode:1980JOSA...70..739B. doi:10.1364/JOSA.70.000739.
• Bhatia, A. B.; Wolf, E. The Zernike circle polynomials occurring in diffraction theory. Proc. Phys. Soc. B. 1952, 65 (11): 909. Bibcode:1952PPSB...65..909B. doi:10.1088/0370-1301/65/11/112.
• ten Brummelaar, T. A. Modeling atmospheric wave aberrations and astronomical instrumentation using the polynomials of Zernike. Opt. Commun. 1996, 132 (3–4): 329. Bibcode:1996OptCo.132..329T. doi:10.1016/0030-4018(96)00407-5.
• Novotni, M.; Klein, R. 3D Zernike Descriptors for Content Based Shape Retrieval (PDF). Proceedings of the 8th ACM Symposium on Solid Modeling and Applications. [2015-01-29]. （原始内容存档 (PDF)于2007-07-29）.
• Novotni, M.; Klein, R. Shape retrieval using 3D Zernike descriptors (PDF). Computer Aided Design. 2004, 36 (11): 1047–1062 [2015-01-29]. doi:10.1016/j.cad.2004.01.005. （原始内容存档 (PDF)于2007-07-29）.
• Farokhi, Sajad; Shamsuddin, Siti Mariyam; Sheikh, U.U; Flusser, Jan. Near Infrared Face Recognition: A Comparison of Moment-Based Approaches (PDF) 291 (1). Springer: 129–135. 2014. doi:10.1007/978-981-4585-42-2_15. |booktitle=被忽略 (帮助)
• Farokhi, Sajad; Shamsuddin, Siti Mariyam; Flusser, Jan; Sheikh, U.U; Khansari, Mohammad; Jafari-Khouzani, Kourosh. Near infrared face recognition by combining Zernike moments and undecimated discrete wavelet transform. Digital Signal Processing. 2014, 31 (1) [2015-01-29]. doi:10.1016/j.dsp.2014.04.008. （原始内容存档于2019-06-02）.