爱因斯坦模型

爱因斯坦模型是一种固体模型，基于三种假设：^[1]:131-132

• 晶格中的每一个原子都是三维量子谐振子；
• 原子不互相作用；
• 所有的原子都以相同的频率振动（与德拜模型不同）。

阿尔伯特·爱因斯坦

第一个假设是相当准确的，而第二个假设则不是。如果原子真的不互相作用，那么声波就不会在固体内传播。

历史上的影响

原先的理论是由爱因斯坦在1907年提出的，具有很大的历史相关性。由杜隆-珀蒂定律所预言的固体的热容已经知道是与经典力学一致的。然而，低温下的实验观察表明，热容在绝对零度时趋于零，在高温时单调增加到杜隆-珀蒂定律的预言。利用普朗克的量子化假设，爱因斯坦第一次能够预言所观察到的实验趋势。与光电效应在一起，这成为需要量子化的最重要的证据之一（值得注意的是，爱因斯坦是在现代量子力学的出现的许多年之前解决了量子谐振子问题）。尽管它成功了，但是爱因斯坦却错误预言为指数趋近于零，而正确的表现则是遵守${\displaystyle T^{3}}$幂定律。这个缺陷后来由德拜模型在1912年纠正。^[2]:389ff

热容（微正则系综）

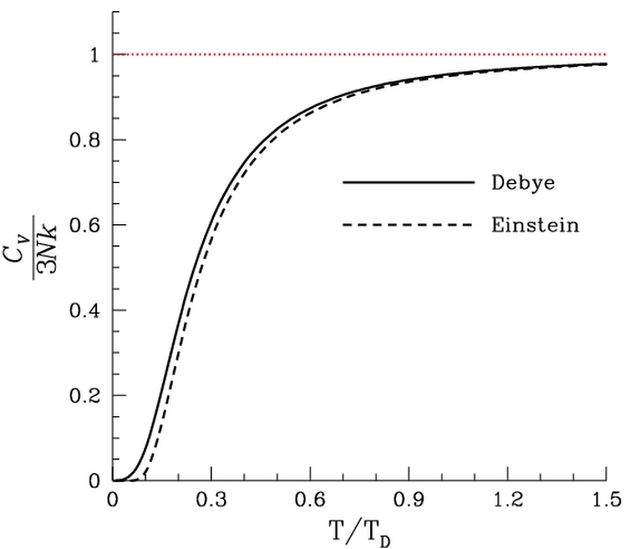
比较德拜、爱因斯坦分别对于热容与温度之间关系的预测。注意到在高温时趋于3Nk的实验值

恒定体积V的物体的热容，通过内能U定义为：

${\displaystyle C_{V}=\left({\partial U \over \partial T}\right)_{V}.}$

${\displaystyle T}$是系统的温度，可以从熵求出：

${\displaystyle {1 \over T}={\partial S \over \partial U}.}$

为了求出熵，考虑由${\displaystyle N}$个原子所组成的固体，每一个原子都有3个自由度。因此，总共有${\displaystyle 3N}$个量子谐振子（以下称SHO）。

${\displaystyle N^{\prime }=3N}$

SHO的可能的能量为：

${\displaystyle E_{n}=\hbar \omega \left(n+{1 \over 2}\right)}$

或者说，能级是均匀分隔的，我们可以定义能量的量子：

${\displaystyle \varepsilon =\hbar \omega }$

它是SHO的能量可以增长的最小的，也是唯一的数量。接着，我们必须计算系统的多重性。也就是说，计算有多少种方法把${\displaystyle q}$个能量量子分布在${\displaystyle N^{\prime }}$个SHO。我们可以想象把${\displaystyle q}$个石头分布在${\displaystyle N^{\prime }}$个盒子中：

或把一堆石头分成${\displaystyle N^{\prime }-1}$份：

或把${\displaystyle q}$个石头和${\displaystyle N^{\prime }-1}$个划分排成一行：

最后一个图最能说明问题。把${\displaystyle n}$ 样东西排成一行，有${\displaystyle n!}$ 种方法。因此，把${\displaystyle q}$个石头和${\displaystyle N^{\prime }-1}$个划分排成一行的方法有${\displaystyle \left(q+N^{\prime }-1\right)!}$ 种，然而，如果把第2个划分和第5个划分互换位置，是没有任何不同的。相同的理由对量子也成立。为了得出可能的不可区分的排列方法，我们必须把排列的总数除以不可区分的排列的数目。一共有${\displaystyle q!}$种相同的量子排列，以及${\displaystyle (N^{\prime }-1)!}$ 种相同的划分排列。因此，系统的多重性为：

${\displaystyle \Omega ={\left(q+N^{\prime }-1\right)! \over q!(N^{\prime }-1)!}}$

正如上面所提及的，这就是把${\displaystyle q}$个能量量子放在${\displaystyle N^{\prime }-1}$个谐振子中的方法数目。系统的熵具有下列形式：

${\displaystyle S/k=\ln \Omega =\ln {\left(q+N^{\prime }-1\right)! \over q!(N^{\prime }-1)!}.}$

${\displaystyle N^{\prime }}$是一个很大的数，把它减去一总体上没有任何影响：

${\displaystyle S/k\approx \ln {\left(q+N^{\prime }\right)! \over q!N^{\prime }!}}$

利用斯特灵公式的帮助，熵可以简化：

${\displaystyle S/k\approx \left(q+N^{\prime }\right)\ln \left(q+N^{\prime }\right)-N^{\prime }\ln N^{\prime }-q\ln q.}$

固体的总能量为：

${\displaystyle U={N^{\prime }\varepsilon \over 2}+q\varepsilon .}$

我们现在来计算温度：

${\displaystyle {1 \over T}={\partial S \over \partial U}={\partial S \over \partial q}{dq \over dU}={1 \over \varepsilon }{\partial S \over \partial q}={k \over \varepsilon }\ln \left(1+N^{\prime }/q\right)}$

把这个公式两边取倒数，以求出U：

${\displaystyle U={N^{\prime }\varepsilon \over 2}+{N^{\prime }\varepsilon \over e^{\varepsilon /kT}-1}.}$

两边关于温度求导，以求出${\displaystyle C_{V}}$：

${\displaystyle C_{V}={\partial U \over \partial T}={N^{\prime }\varepsilon ^{2} \over kT^{2}}{e^{\varepsilon /kT} \over \left(e^{\varepsilon /kT}-1\right)^{2}}}$

或

${\displaystyle C_{V}=3Nk\left({\varepsilon \over kT}\right)^{2}{e^{\varepsilon /kT} \over \left(e^{\varepsilon /kT}-1\right)^{2}}}$

虽然固体的爱因斯坦模型准确预言高温时的热容，在低温时与实验值仍有明显的差距。关于低温时准确的热容计算，参见德拜模型。

热容（正则系综）

热容可以通过利用SHO的正则配分函数来获得。

${\displaystyle Z=\sum _{n=0}^{\infty }e^{-E_{n}/kT}}$

其中

${\displaystyle E_{n}=\varepsilon \left(n+{1 \over 2}\right)}$

把该式代入配分函数的公式，得：

${\displaystyle {\begin{aligned}Z&{}=\sum _{n=0}^{\infty }e^{-\varepsilon \left(n+1/2\right)/kT}=e^{-\varepsilon /2kT}\sum _{n=0}^{\infty }e^{-n\varepsilon /kT}=e^{-\varepsilon /2kT}\sum _{n=0}^{\infty }\left(e^{-\varepsilon /kT}\right)^{n}\\&{}={e^{-\varepsilon /2kT} \over 1-e^{-\varepsilon /kT}}={1 \over e^{\varepsilon /2kT}-e^{-\varepsilon /2kT}}={1 \over 2\sinh \left({\varepsilon \over 2kT}\right)}.\end{aligned}}}$

这是一个SHO的配分函数。因为，统计上来说，固体的热容、能量，以及熵，都是在它的原子（SHO）中均匀分布的，因此我们可以利用这个配分函数来获得这些物理量，然后直接把它们乘以${\displaystyle N^{\prime }}$以得出总量。接着，我们来计算每一个谐振子的平均能量：

${\displaystyle \langle E\rangle =u=-{1 \over Z}\partial _{\beta }Z}$

其中

${\displaystyle \beta ={1 \over kT}.}$

因此：

${\displaystyle u=-2\sinh \left({\varepsilon \over 2kT}\right){-\cosh \left({\varepsilon \over 2kT}\right) \over 2\sinh ^{2}\left({\varepsilon \over 2kT}\right)}{\varepsilon \over 2}={\varepsilon \over 2}\coth \left({\varepsilon \over 2kT}\right).}$

于是，一个谐振子的热容为：

${\displaystyle C_{V}={\partial U \over \partial T}=-{\varepsilon \over 2}{1 \over \sinh ^{2}\left({\varepsilon \over 2kT}\right)}\left(-{\varepsilon \over 2kT^{2}}\right)=k\left({\varepsilon \over 2kT}\right)^{2}{1 \over \sinh ^{2}\left({\varepsilon \over 2kT}\right)}.}$

整个固体的热容由${\displaystyle C_{V}=3NC_{V}}$给出：

${\displaystyle C_{V}=3Nk\left({\varepsilon \over 2kT}\right)^{2}{1 \over \sinh ^{2}\left({\varepsilon \over 2kT}\right)}.}$

它与前面推导的公式是相等的。

物理量${\displaystyle T_{E}=\varepsilon /k}$的量纲是温度，是晶体的一个特有的性质。它称为“爱因斯坦温度”。因此，爱因斯坦晶体模型预言晶体的能量和热容是无量纲比率${\displaystyle T/T_{E}}$的通用函数。类似地，德拜模型预言了比率${\displaystyle T/T_{D}}$的通用函数。