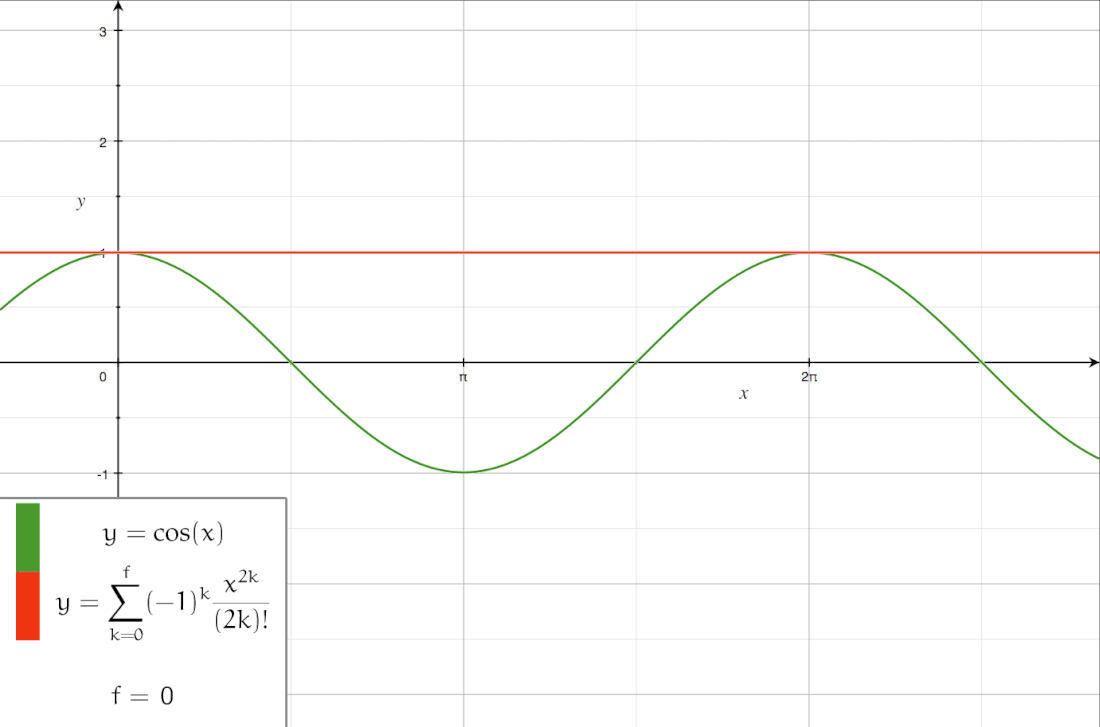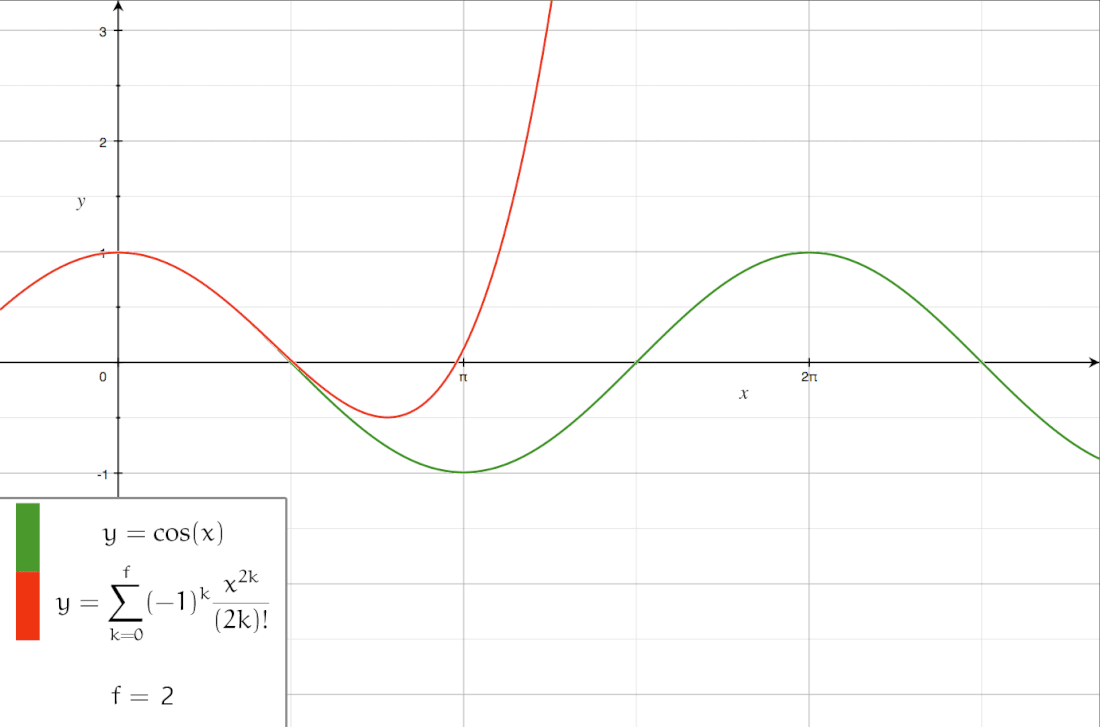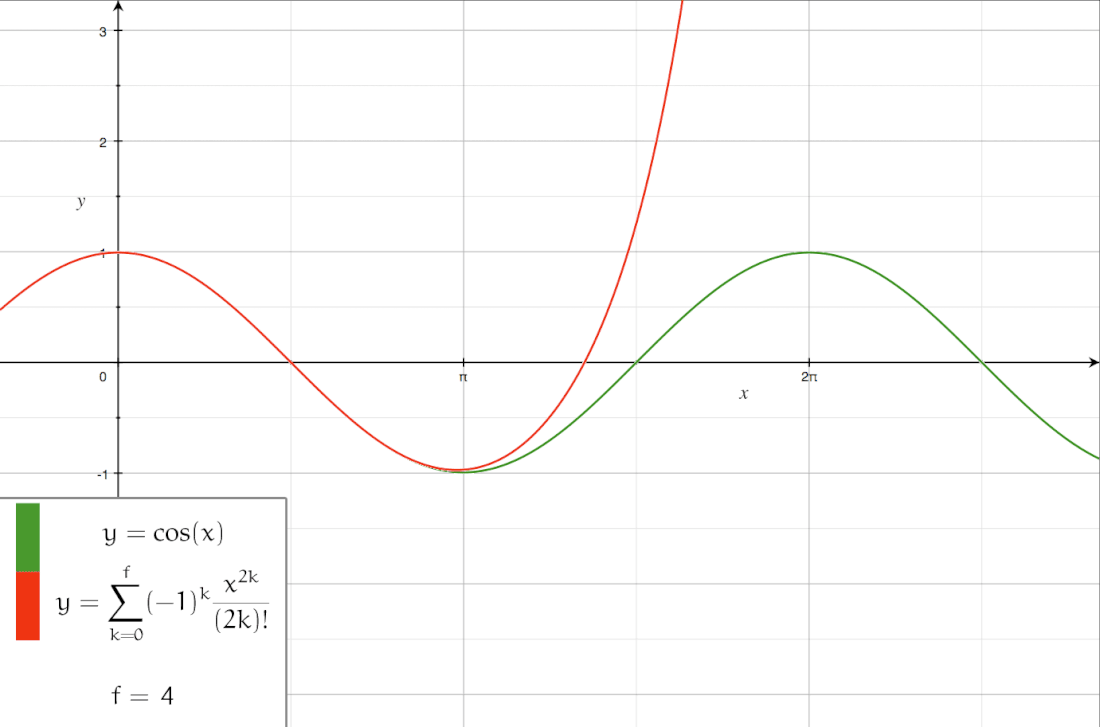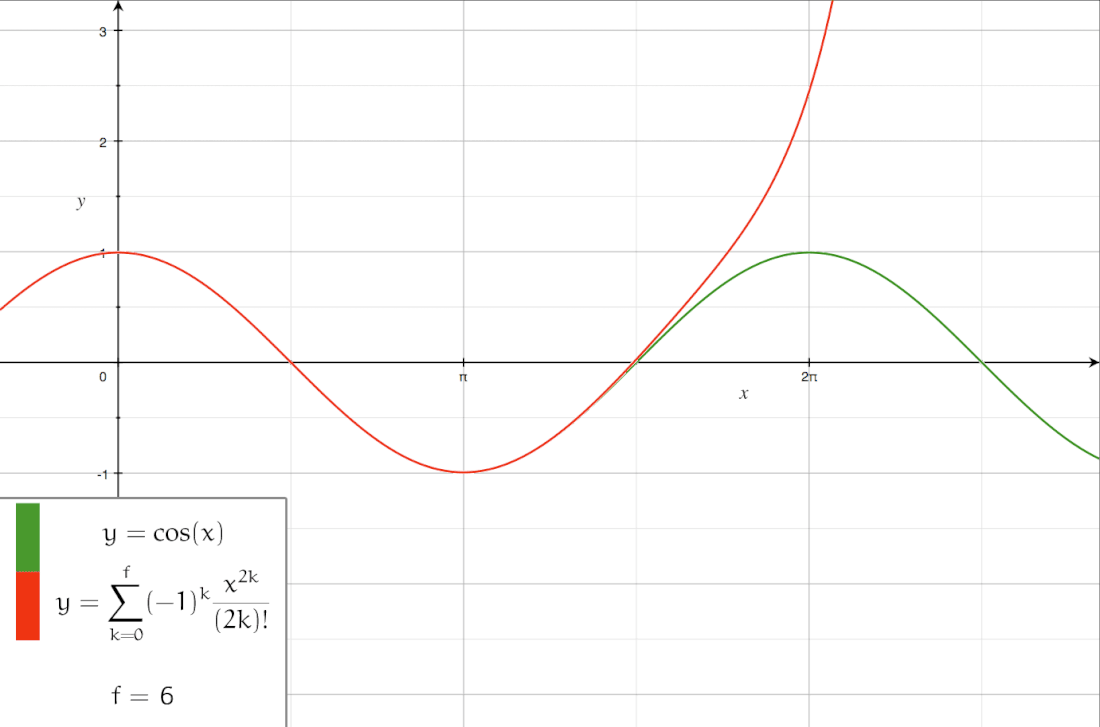
这里介绍了若干种级数展开的方式:
泰勒级数是基于函数在一个点上的导数的幂级数。具体来说,如果函数  在
在 附近是无限可微的,那么
附近是无限可微的,那么 在该点周围的泰勒级数为
在该点周围的泰勒级数为 ,按照惯例
,按照惯例 。
。 的麦克劳林级数是其在
的麦克劳林级数是其在 处的泰勒数列。洛朗级数是泰勒级数的延伸,允许负指数项;它的形式是
处的泰勒数列。洛朗级数是泰勒级数的延伸,允许负指数项;它的形式是  并在环内收敛。
并在环内收敛。
广义狄利克雷级数具有  的形式。它的一个重要特例是狄利克雷级数
的形式。它的一个重要特例是狄利克雷级数 。
。 傅里叶级数将周期函数展开成许多正弦和余弦函数之和。更具体地,一个周期为
傅里叶级数将周期函数展开成许多正弦和余弦函数之和。更具体地,一个周期为 的函数
的函数 的傅里叶级数为:
的傅里叶级数为:

其中系数为:

 在声学中,基音和泛音共同构成了一个傅里叶数列的例子。
在声学中,基音和泛音共同构成了一个傅里叶数列的例子。
斯特林公式 是对数Γ函数的一个近似值。
是对数Γ函数的一个近似值。