逆序对

在计算机科学和离散数学中，一个序列的逆序（inversion）对，是失去自然次序的元素对。

这个置换中的一个逆序对，表示为位置对（2,4）或元素对（5,2）。
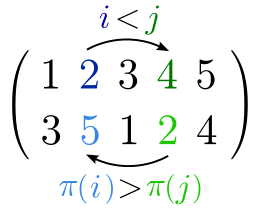
这个置换的逆序，使用基于位置表示法表示为：(1, 3), (1, 4), (2, 3), (2, 4)和(2, 5)；
或者使用基于元素表示法表示为：(3, 1), (3, 2), (5, 1), (5, 2)和(5, 4)。

定义

逆序

一个四元素置换的从基于位置逆序到基于元素逆序的映射。

设${\displaystyle \ \pi \ }$为一个排列，如果${\displaystyle \ i<j\ }$而且${\displaystyle \ \pi (i)>\pi (j)\ }$， 这个位置（有称为“序位”）对${\displaystyle \ (i,j)\ }$^[1][2]，或者这个元素对${\displaystyle \ {\bigl (}\pi (i),\pi (j){\bigr )}\ }$^[3][4][5]，被称为是${\displaystyle \ \pi \ }$的一个逆序。

逆序集是所有逆序的集合。一个排列${\displaystyle \ \pi \ }$的使用基于位置表示法的逆序集，相同于其反向排列${\displaystyle \ \pi ^{-1}\ }$的使用基于元素表示法的逆序集，只有每个有序对的两个分量交换位置，反之亦然^[6]。

通常逆序是对于排列的定义，但也可以用于序列： 设${\displaystyle \ S\ }$是一个序列（或多重集排列^[7]）。如果${\displaystyle \ i<j\ }$而且${\displaystyle \ S(i)>S(j)\ }$， 这个位置对${\displaystyle \ (i,j)\ }$^[7][8]，或者这个元素对${\displaystyle \ {\bigl (}S(i),S(j){\bigr )}\ }$^[9]，被称为是${\displaystyle \ S\ }$的一个逆序。

对于序列，根据基于元素定义的逆序不是唯一性的，因为不同的位置对上可能有相同的值对。

逆序数

序列${\displaystyle \ X=\langle x_{1},\dots ,x_{n}\rangle \ }$的逆序数${\displaystyle \ {\mathtt {inv}}(X)\ }$^[10]，是逆序集的势，它常用于量度排列^[5]或序列^[9]的已排序程度（有时叫做预排序度presortedness）。逆序数在${\displaystyle \ 0\ }$至${\displaystyle \ {\frac {n(n-1)}{2}}\ }$之间，含二者。

在一个排列的箭头指向图中，它是箭头指向相交叉的数^[6]，也是从单位排列而得到的Kendall tau距离（英语：Kendall tau distance），以及每个与逆序有关的向量之和，它们在后面章节中定义。

对于逆序数，基于位置与基于元素定义之间的分别并不重要，因为排列及其反向排列都具有相同的逆序数。

其它测量（预先）排序程度的方式，包括了为排好序列而从序列中可以删除元素的最小数量，对序列所“运行”排序的次数和长度，每个元素在已排序位置之上的距离总和（Spearman footrule），以及排序过程中必需的最少交换次数^[11]。比较排序算法计算逆序数的时间为${\displaystyle \ O(n\log n)\ }$^[12]。

目前求逆序对数目比较普遍的方法，是利用归并排序做到${\displaystyle \ O(n\log n)\ }$的时间复杂度；也可以利用树状数组、线段树来实现这种基础功能。复杂度均为${\displaystyle \ O(n\log n)\ }$。

逆序有关的向量

有三个类似的向量用于将排列的逆序，压缩到能唯一确定它的这个向量中。它们通常被称为逆序向量或Lehmer码（英语：Lehmer code）。这里的定义及公式来源于逆序 (离散数学)。

本文将逆序向量记为${\displaystyle \ v\ }$^[13]，其它的两个向量有时分别称为“左”和“右”逆序向量；为了避免与前面的逆序向量混淆，本文将另两个分别称为“左逆序计数”${\displaystyle \ l\ }$和“右逆序计数”${\displaystyle \ r\ }$。左逆序计数是以反向colexicographic次序的排列^[14]，右逆序计数则是以字典序的排列。

Rothe图

逆序向量${\displaystyle \ v\ }$：
采用基于元素的定义，${\displaystyle \ v(i)\ }$是有序对较小（右）分量为${\displaystyle \ i\ }$的逆序数^[3]。

${\displaystyle \ v(i)\ }$是在${\displaystyle \ \pi \ }$之中于${\displaystyle \ i\ }$之前，大于${\displaystyle \ i\ }$的元素的数量。

${\displaystyle v(i)~~=~~\#\{k\mid k>i~\land ~\pi ^{-1}(k)<\pi ^{-1}(i)\}}$

其更符合直觉的定义方式为：

${\displaystyle \ v{\bigl (}\pi (i){\bigr )}\ }$是在${\displaystyle \ \pi \ }$之中于${\displaystyle \ \pi (i)\ }$之前，大于${\displaystyle \ \pi (i)\ }$的元素的数量。

${\displaystyle v{\bigl (}\pi (i){\bigr )}~~=~~\#\{k\mid k<i~\land ~\pi (k)>\pi (i)\}~~=~~l(i)}$

后者定义也适用于没有反向对应者的序列。

左逆序计数${\displaystyle \ l\ }$：
采用基于位置的定义，${\displaystyle \ l(i)\ }$是有序对较大（右）分量为${\displaystyle \ l(i)\ }$的逆序数。

${\displaystyle \ l(i)\ }$是在${\displaystyle \ \pi (i)\ }$之中于${\displaystyle \ \pi (i)\ }$之前，大于${\displaystyle \ \pi (i)\ }$的元素的数量。

${\displaystyle l(i)~~=~~\#\left\{k\mid k<i~\land ~\pi (k)>\pi (i)\right\}}$

右逆序计数${\displaystyle \ r\ }$，通常称为Lehmer码：
采用基于位置的定义，${\displaystyle \ r(i)\ }$是有序对较小（左）分量为${\displaystyle \ i\ }$的逆序数。

${\displaystyle \ r(i)\ }$是${\displaystyle \ \pi (i)\ }$之中于${\displaystyle \ \pi (i)\ }$之后，小于${\displaystyle \ \pi (i)\ }$的元素的数量。

${\displaystyle r(i)~~=~~\#\{k\mid k>i~\land ~\pi (k)<\pi (i)\}}$

${\displaystyle \ l\ }$和${\displaystyle \ v\ }$之间的关系：

${\displaystyle v(i)~~=~~l{\bigl (}\pi ^{-1}(i){\bigr )}}$

${\displaystyle l(i)~~=~~v{\bigl (}\pi (i){\bigr )}}$

${\displaystyle \ l\ }$的第一个数字和${\displaystyle \ v\ }$的最后一个数字总是${\displaystyle \ 0\ }$，可以省略。

Rothe图可以协助找出${\displaystyle \ v\ }$和${\displaystyle \ r\ }$。Rothe（英语：Heinrich August Rothe）图是以黑点来表示1的排列矩阵，每一个位置上若为逆序（通常以叉号表示），则在其右侧与下方即有一点。${\displaystyle \ r(i)\ }$是图中第${\displaystyle \ i\ }$列排列逆序的加总，而${\displaystyle \ v(i)\ }$是${\displaystyle \ i\ }$栏中排列逆序的加总。排列矩阵的逆矩阵即是此矩阵的转置矩阵，因此某一排列的${\displaystyle \ v\ }$即是它转置矩阵的${\displaystyle \ r\ }$，反之亦然。

${\displaystyle \ r\ }$和${\displaystyle \ l\ }$之间的关系：

${\displaystyle \pi (i)~~=~~i+r(i)-l(i)}$

范例：四个元素的全部排列

四个元素的6种可能逆序

下面可排序表显示了四个元素的集合，它的逆序集会有不同位置的24种排列、逆序相关向量和逆序数（右栏是它的反向排列，用于以colex排序）。可以看出${\displaystyle \ v\ }$和${\displaystyle \ l\ }$的位数总是相同，而${\displaystyle \ l\ }$和${\displaystyle \ r\ }$与位逆序集有关。 最右侧栏是排列左上右下对角线的总和，如三角形图示，以及${\displaystyle \ r\ }$是左下右上对角线的总和（配对在下降对角线中其右侧都是${\displaystyle \ 2,3,4\ }$组成，而在上升对角线中的左侧都是${\displaystyle \ 1,2,3\ }$组成）。 此表中${\displaystyle \ \pi \ }$的预设排序是反向colex次序，这与${\displaystyle \ l\ }$的colex次序相同。${\displaystyle \ \pi \ }$的字典序与${\displaystyle \ r\ }$的字典序相同。

用于比较的三个元素全部排列表
0 1 2 3 4 5 ${\displaystyle \pi }$ ${\displaystyle v}$ ${\displaystyle l}$ p-b ${\displaystyle r}$ # 0 123 321 000 000 000 000 000 000 0 1 213 312 100 001 010 010 100 001 1 2 132 231 010 010 100 001 010 010 1 3 312 213 110 011 110 011 200 002 2 4 231 132 200 002 200 002 110 011 2 5 321 123 210 012 210 012 210 012 3

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

${\displaystyle \pi }$ ${\displaystyle v}$ ${\displaystyle l}$ p-b ${\displaystyle r}$ # 0 1234 4321 0000 0000 0000 0000 0000 0000 0 1 2134 4312 1000 0001 0010 0100 1000 0001 1 2 1324 4231 0100 0010 0100 0010 0100 0010 1 3 3124 4213 1100 0011 0110 0110 2000 0002 2 4 2314 4132 2000 0002 0200 0020 1100 0011 2 5 3214 4123 2100 0012 0210 0120 2100 0012 3 6 1243 3421 0010 0100 1000 0001 0010 0100 1 7 2143 3412 1010 0101 1010 0101 1010 0101 2 8 1423 3241 0110 0110 1100 0011 0200 0020 2 9 4123 3214 1110 0111 1110 0111 3000 0003 3 10 2413 3142 2010 0102 1200 0021 1200 0021 3 11 4213 3124 2110 0112 1210 0121 3100 0013 4 12 1342 2431 0200 0020 2000 0002 0110 0110 2 13 3142 2413 1200 0021 2010 0102 2010 0102 3 14 1432 2341 0210 0120 2100 0012 0210 0120 3 15 4132 2314 1210 0121 2110 0112 3010 0103 4 16 3412 2143 2200 0022 2200 0022 2200 0022 4 17 4312 2134 2210 0122 2210 0122 3200 0023 5 18 2341 1432 3000 0003 3000 0003 1110 0111 3 19 3241 1423 3100 0013 3010 0103 2110 0112 4 20 2431 1342 3010 0103 3100 0013 1210 0121 4 21 4231 1324 3110 0113 3110 0113 3110 0113 5 22 3421 1243 3200 0023 3200 0023 2210 0122 5 23 4321 1234 3210 0123 3210 0123 3210 0123 6

排列的弱次序

对称群的Permutohedron S₄

n物品排列的集合其部分次序的结构，称为排列的弱次序，而构成格。 以逆序集的子集关系绘出的哈斯图，则构成了称为permutohedron的骨架。 如果依位置将某一排列分配给每个逆序集，所得到的排序是permutohedron的次序，其中的边对应于连续两元素的交换。这是排列的弱排序。The identity is its minimum, and the permutation formed by reversing the identity is its maximum. 如果依元素将某一排列分配给每个逆序集，所得到的排序将是凯莱图的次序，其中的边对应于连续两元素的交换。对称组的凯莱图与其permutohedron相似，但是每个排列由其反向替换。

参见

• 阶乘进制
• 置换群
• 置换的奇偶性