龙伯透镜

龙伯透镜（Luneburg lens），是一种球面对称梯度折射率透镜。它由无损介电材料制成的实心球体组成，其介电常数与位置相关。如果其背面是镜面，它会将入射的平行波准确地反射到其源头方向，从而充当反射器的作用。典型的龙伯透镜的折射率n从中心到外表面呈径向减小。它们可用于从可见光到无线电波的电磁辐射。

标准龙伯透镜的横截面

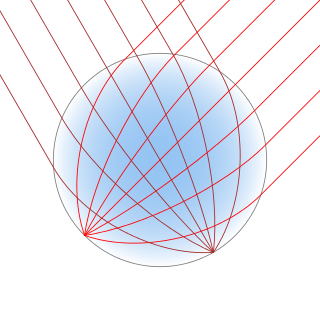
对于某些折射率分布，透镜将形成两个给定同心球的完美几何图像。有无数种折射率分布可以产生这种效果。最简单的解决方案是由数学家鲁道夫·龙伯（英语：Rudolf Luneburg）于1944年提出的。^[1] 龙伯的折射率解决方案在透镜外产生两个共轭焦点。如果一个焦点位于无穷远处，另一个焦点位于透镜的另一侧表面，则该解决方案采用简单而明确的形式。J. Brown和A. S. Gutman随后提出了产生一个内部焦点和一个外部焦点的解决方案。^[2][3] 这些解决方案并不是唯一的；解决方案集由一组必须进行数值评估的定积分定义。^[4]

龙伯透镜是由若干层介电常数不同的材料制成的介质球，能使照射在透镜上的电磁波，通过透镜聚焦在金属反射面的内表面上，经过反射，将反射波通过透镜返回发射源方向。主要用以产生假目标欺骗雷达。龙伯透镜反射器具有体积小，雷达截面积比相同尺寸的角反射器大，在水平和垂直方向上具有较宽的反射方向图等优点，但重量重、造价贵、制造工艺复杂。^[5]

设计

龙伯解决方案

当光源位于其边缘时，龙伯透镜会将点光源转换为准直光束。

理想龙伯透镜表面上的每个点都是入射到对侧的平行辐射的焦点。理想情况下，根据以下公式，透镜组成材料的介电常数${\displaystyle \epsilon _{r}}$从中心的2降至表面的1（或者等效地，折射率${\displaystyle n}$从${\displaystyle {\sqrt {2}}}$降至1）

${\displaystyle n={\sqrt {\epsilon _{r}}}={\sqrt {2-\left({\frac {r}{R}}\right)^{2}}},}$

其中${\displaystyle R}$为透镜的半径。由于表面的折射率与周围介质的折射率相同，因此表面不会发生反射。在透镜内，光线的路径是椭圆弧。

麦克斯韦的鱼眼透镜

麦克斯韦鱼眼透镜的横截面，蓝色阴影表示折射率增加.

麦克斯韦的鱼眼透镜 (Maxwell's fish-eye lens) 也是广义龙伯透镜的一个例子。鱼眼透镜最早由麦克斯韦于1854年^[6]完整描述（因此早于龙伯透镜的出现），其折射率根据以下公式变化

${\displaystyle n(r)={\sqrt {\epsilon _{r}}}={\frac {n_{0}}{1+\left({\frac {r}{R}}\right)^{2}}},}$

其中${\displaystyle n_{0}}$是透镜中心的折射率，而${\displaystyle R}$是透镜球面的半径。^[7] 透镜表面的折射率为${\displaystyle n_{0}/2}$。透镜将球面上的每个点都成像到表面上的相对点。在透镜内，光线的路径是圆弧。

应用

实际上，龙伯透镜通常是由离散同心壳组成的分层结构，每个壳的折射率不同。这些壳形成阶梯式折射率分布，与龙伯解决方案略有不同。这种透镜通常用于微波频率，尤其是用于构建高效的微波天线和雷达校准标准。龙伯透镜的圆柱形类似物也用于准直来自激光二极管的光。

雷达反射镜

通过对龙伯透镜的部分表面进行金属化处理，可将其制成雷达反射镜。来自远处雷达发射机的辐射被聚焦到透镜另一侧金属化的底部；在这里，辐射被反射，并被聚焦回雷达站。这种方案的一个难点是，金属化区域会阻止辐射进入或离开透镜的这一部分，而非金属化区域则会在反面形成一个盲点。

微波天线

龙伯透镜可用作高增益无线电天线的基础。这种天线与碟形天线类似，但使用透镜而不是抛物面反射器作为主要聚焦元件。与碟形天线一样，接收器或发射器的馈电也放置在焦点处，馈电通常由喇叭天线组成。^[8] 馈源喇叭的相位中心必须与聚焦点重合，但由于相位中心总是在喇叭口内侧，因此不能紧贴镜头表面。因此，有必要使用一种聚焦在表面之外的龙伯透镜，而不是聚焦在表面上的传统透镜。

参阅

• 声响诱饵
• 超材料