三侧锥三角柱

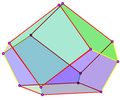
三侧锥三角柱（Triaugmented triangular prism）又称四角化三角柱（Tetrakis triangular prism）^[1]:41，由14个正三角形组成，由于这种多面体的面都是三角形，因此是一种十四面的三角面多面体^[2]，其亦属于詹森多面体之一，索引为J₅₁^[2]。形如其名地，它可由三个正四角锥（J₁）以底面黏合在一个正三角柱的侧面上组合而成，这与侧锥三角柱（J₄₉）和二侧锥三角柱（J₅₀）有著极为相似的构造。詹森多面体是凸多面体，面皆由正多边形组成但不属于均匀多面体，共有92种。这些立体最早在1966年由诺曼·詹森（Norman Johnson）命名并给予描述^[3]。

三侧锥三角柱

类别	詹森多面体 J50 - J51 - J52
对偶多面体	结合多面体（英语：Associahedron） K5
识别
名称	三侧锥三角柱
参考索引	J51
鲍尔斯缩写 （verse-and-dimensions的wikia：Bowers acronym）	tautip
数学表示法
康威表示法	k4P3
性质
面	14
边	21
顶点	9
欧拉特征数	F=14, E=21, V=9 （χ=2）
组成与布局
面的种类	14个三角形
顶点图	3个(34) 6个(35)
对称性
对称群	D3h群
特性
凸多面体、 三角形多面体
图像
结合多面体（英语：Associahedron） K5 （对偶多面体） （展开图）

性质

三侧锥三角柱共由14个面、21条边和9个顶点组成^[4][5][6]。组成三侧锥三角柱的14个面都是正三角形。在其9个顶点中，有3个顶点是4个三角形的公共顶点^[6]，在顶点图中可以用[3⁴]来表示^[7]、另外6个顶点是5个三角形的公共顶点^[6]，在顶点图中可以用[3⁵]来表示^[7]。

体积与表面积

若一个三侧锥三角柱边长为${\displaystyle a}$，则其体积${\displaystyle V}$与表面积${\displaystyle A}$为：^[8][2]

${\displaystyle V={\frac {2{\sqrt {2}}+{\sqrt {3}}}{4}}a^{3}\approx 1.14012a^{3}}$

${\displaystyle A={\frac {7{\sqrt {3}}}{2}}a^{2}\approx 6.06218a^{2}}$

二面角

三侧锥三角柱有3种二面角，这三种二面角皆为三角形和三角形的二面角，但位置不同，其角度分别为：

位于两个相异侧锥侧面的交角角度为：^[7]

${\displaystyle \arccos \left(-{\frac {1+2{\sqrt {6}}}{6}}\right)\approx 2.957830\approx 169.471221^{\circ }}$

位于底面和侧锥侧面的交角角度为负根号三分之二的反馀弦值，约为144.7356度：^[7]

${\displaystyle \arccos \left(-{\sqrt {\frac {2}{3}}}\right)\approx 2.52611294\approx 144.735610^{\circ }}$

位于同个侧锥侧面的交角角度为负三分之一的反馀弦值，约为109.471度：^[7]

${\displaystyle \arccos \left(-{\frac {1}{3}}\right)\approx 1.9106332\approx 109.471221^{\circ }}$

顶点座标

三侧锥三角柱的顶点座标为：^[2]

${\displaystyle \left(\pm {\frac {1}{2}},\,\pm {\frac {1}{2}},\,0\right)}$

${\displaystyle \left(0,\,0,\,{\frac {\sqrt {2}}{2}}\right)}$

${\displaystyle \left(0,\,\pm {\frac {1}{2}},\,-{\frac {\sqrt {3}}{2}}\right)}$

${\displaystyle \left(\pm {\frac {1+{\sqrt {6}}}{4}},\,0,\,-{\frac {{\sqrt {2}}+{\sqrt {3}}}{4}}\right)}$

最后一个座标的x和z值可透过解下列方程式获得：^[2]

${\displaystyle x^{2}+\left({\frac {1}{2}}\right)^{2}+\left(z+{\frac {\sqrt {3}}{2}}\right)^{2}=1^{2}}$

${\displaystyle \left(x-{\frac {1}{2}}\right)^{2}+\left({\frac {1}{2}}\right)^{2}+z^{2}=1^{2}}$

对偶多面体

三侧锥三角柱的对偶多面体为截四阶角双三角锥（order-4 truncated triangular bipyramid），又称底面截角双三角锥（base-truncated triangular bipyramid）^[9]或5阶结合多面体（英语：Associahedron）。

参见

• 詹森多面体
• 正四角锥
• 侧锥三角柱
• 二侧锥三角柱
• 多面体