切比雪夫连杆机构

切比雪夫连杆机构（Chebyshev linkage）是一种可将旋转运动转换为近似直线运动的连杆机构，属于平面四杆机构，且其构形中有出现交叉四边形。

切比雪夫连杆机构

切比雪夫连杆机构是由十九世纪的数学家巴夫努提·列沃维奇·切比雪夫所发明，他研究的主题是运动学的理论问题。其中一个问题是建构可以将旋转运动转换为近似直线运动的连杆。詹姆斯·瓦特在改进其蒸汽机时，也曾研究过此一主题^[1]。

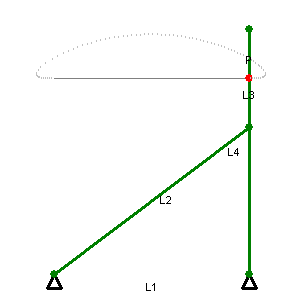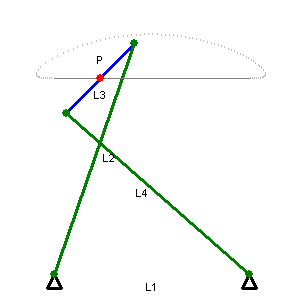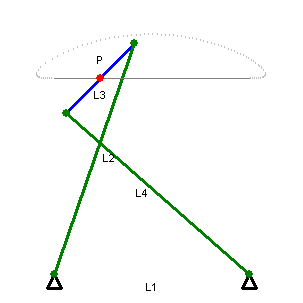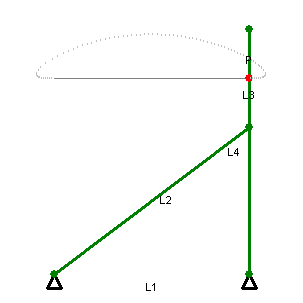
直线运动的连杆会限制点P–杆L₃的中点–在二个极限位置中间的直线上。（L₁, L₂, L₃和L₄如图所示）。在这段行程范围中，P的轨迹近似直线，只有少许的偏移。各杆的比例为

${\displaystyle L_{1}:L_{2}:L_{3}=2:2.5:1=4:5:2.\,}$

点P是L₃的中点。上述关系确保当连杆在直线行程的极限位置时，L₃会是垂直的。^[2]

各杆长度的关系如下：

${\displaystyle L_{4}=L_{3}+{\sqrt {L_{2}^{2}-L_{1}^{2}}}.\,}$

可以证明若各杆的比例如上，则下式成立

${\displaystyle L_{4}=L_{2}.\,}$

且可以让P有近似直线的轨迹。

运动方程

可以找出连杆随输入角变化的运动方程，随著输入角的变化，其速度及受力也随之改变。输入角可以是L₂相对水平线的角度，或是L₄相对水平线的角度。不论输入角为何，都可以计算连杆L₃中点的轨迹，假设L₃靠右侧的端点为A，靠左侧的端点为B，而其中点为P，以L₂不动的端点为原点，可得A的方程^[2]：

${\displaystyle x_{A}=L_{2}\cos(\varphi _{1})\,}$

${\displaystyle y_{A}=L_{2}\sin(\varphi _{1})\,}$

点B的运动可以用另一个角来计算

${\displaystyle x_{B}=L_{1}-L_{4}\cos(\varphi _{2})\,}$

${\displaystyle y_{B}=L_{4}\sin(\varphi _{2})\,}$

最终，可以得到输出角和输入角之间的关系：

${\displaystyle \varphi _{2}=\arcsin \left[{\frac {L_{2}\,\sin(\varphi _{1})}{\overline {AO_{2}}}}\right]-\arccos \left({\frac {L_{4}^{2}+{\overline {AO_{2}}}^{2}-L_{3}^{2}}{2\,L_{4}\,{\overline {AO_{2}}}}}\right)\,}$

其中的${\displaystyle {\overline {AO_{2}}}}$是A点和O₂点之间的直线距离。

${\displaystyle {\overline {AO_{2}}}={\sqrt {L_{1}^{2}+L_{2}^{2}-2L_{1}L_{2}\cos(\varphi _{1})}}\,}$

依照上式可以写出P点的方程。

${\displaystyle x_{P}={\frac {x_{A}+x_{B}}{2}}\,}$

${\displaystyle y_{P}={\frac {y_{A}+y_{B}}{2}}\,}$

输入角

极限位置的说明

在维持近似直线运动的情形下，输入角的极限分别是：

${\displaystyle \varphi _{\text{min}}=\arccos \left({\frac {4}{5}}\right)\approx 36.8699^{\circ }.\,}$

${\displaystyle \varphi _{\text{max}}=\arccos \left({\frac {-1}{5}}\right)\approx 101.537^{\circ }.\,}$

相关条目

切比雪夫λ连杆机构（蓝色和绿色）可以产生几乎直线的轨迹

• 切比雪夫λ连杆机构（英语：Chebyshev's Lambda Mechanism）
• 瓦特氏直线运动机构（英语：Watt's linkage），类似的直线机构。
• 直线运动机构
• Scott Russell机构（英语：Scott Russell linkage）
• 霍肯连杆机构（英语：Hoeckens linkage）：产生近似直线轨迹的四杆机构
• 波塞利耶-利普金机械：产生直线轨迹的八杆机构