加法

加法（英语、法语：addition）是基本的算术运算之一，与减法、乘法、除法合称“四则运算”。加法运算的本质，就是“一个以上的量的合并”。

“加”重定向至此。关于其他用法，请见“加 (消歧义)”。

如图，三个苹果和两个苹果被组合在一起，共有五个苹果，用数学表达式表示成${\displaystyle 3+2=5}$，即“3加2等于5”。

除了自然数，其他类型的数也可以定义加法，例如整数、实数、复数等，这些类型的加法是算术的一部分。在代数中，许多抽象的概念也可以相加，例如向量、矩阵等。

将多个一相加的动作被称为计数；一个数加零仍等于自身。当与相关的运算（像是减法、乘法等）同时出现时，加法也遵循一些法则。

加法是最简单的数学任务之一。蹒跚学步的小孩就能将较小的数正确相加；最基本的${\displaystyle 1+1=2}$连五个月大的婴儿都会，甚至其他种类的动物也会算。在初等教育中，学生使用十进制或二进制进行加法运算，从个位数的加法开始，逐渐变难。辅助加法的机械从古代的算盘，到现今的电子计算机，种类繁多。至今，人们还在研究在电子计算机上实现加法的高效算法。

定义

为证明加法的常见性质，首先必须给出加法的准确定义。

加法首先在自然数范围内定义。接着，在集合论中，加法被拓展至更加广阔的集合：整数，有理数，实数……

集合的“合并”

以不同图形展示的集合合并

加法最基础的诠释，或源于对集合的朴素合并：^[1]

当两个及以上互不相交的集合（即不交集）合并为单一集合时，该单一集合中的对象数量等于原集合中对象数量的总和。

该诠释易于直观呈现，且几乎不存在歧义。在高等数学中，它还为更严格的定义奠定基础。然而，如何将该诠释延伸至包含分数或负数的情形则并不显见^[2]。一种可行思路是考虑易分割的对象集合，例如派饼；另一种可行思路或为更优的方案——分段式杆件。相较于单纯合并杆件分段，更可采取杆件首尾相接的组合方式，由此接引加法的另一种定义：所叠加的并非杆件本身，而是杆件的长度。^[3]

长度的“延伸”

加法 2 + 4 = 6 在数轴上的视觉化版本。向右平移 2 个单位，再向右平移 4 个单位，就是向右平移 6 个单位。

加法 2 + 4 = 6 在数轴上的视觉化版本。向右平移 4 个单位相当于向右平移 1 个单位 4 次。

加法的第二种诠释，源于通过给定新长度延伸初始长度：^[4]

当初始长度延伸一定量时，最终长度等于初始长度与延伸长度之和。

和式 ${\displaystyle a+b}$ 可解释为代数上结合 ${\displaystyle a}$ 与 ${\displaystyle b}$ 的二元运算，亦可理解为向 ${\displaystyle a}$ 增添 ${\displaystyle b}$ 个单位。在该诠释下，和式 ${\displaystyle a+b}$ 的各组成部分具有非对称作用，该运算可视作对 ${\displaystyle a}$ 施加一元运算 ${\displaystyle +b}$ ^[5]。相较于将 ${\displaystyle a}$ 与 ${\displaystyle b}$ 均称为加数，将 ${\displaystyle a}$ 称为“被加数”显然更妥当，因其扮演被动角色。

一元视角在讨论减法时亦具效用，因每个一元加法运算均有对应的逆向一元减法运算，反之亦然。

符号与表示

主条目：加号

加号“+”（Unicode：U+002B；ASCII：+）是拉丁词语“et”（和）的缩写，它在数学中的使用至少可以追溯到1489年。

加法通过在各项之间加号“+”表示（中缀表示法的其中一种），运算结果用等号“=”表示。例如：

加号

${\displaystyle {{1}+{1}}=2}$（1 加 1 等于 2）

${\displaystyle {{2}+{2}}=4}$（2 加 2 等于 4）

${\displaystyle {{1}+{2}}=3}$（1 加 2 等于 3）

${\displaystyle {{{5}+{4}}+{2}}=11}$（见结合律）

${\displaystyle {{{{3}+{3}}+{3}}+{3}}=12}$（见乘法）

当一个整数紧接一个分数时，表示两者的和，此类形式称为带分数。例如：^[6]

${\displaystyle 3{1 \over 2}=3+{1 \over 2}=3.5}$

该记法可能引发混淆，因为在大多数其他数学语境中，符号并置（英语：Juxtaposition#Mathematics）通常表示乘法而非加法。^[7]

The Art of Nombryng（15 世纪）是最早的英语算术书之一，此图为重绘的插图。

一般加法运算中，待相加的数字或对象统称为项（term）^[8]或加数（addend 或 summand）^[1]，结果称为和（sum），此术语体系同样适用于多项求和情形，但需与乘法运算中的因数（factors）明确区分。有些人将第一个加数称为被加数（augend）^[9]。事实上，在文艺复兴时期，许多学者根本不将首个加数视为“加数”。而今由于了解加法交换律的普遍性，“被加数”一词已鲜少使用，两项通常统称为加数。^[10]

英语单词 addition（加法，名词） 和 add（加，动词）源自拉丁语动词 addere，它是由介词 ad 和动词 dare 组成的合成词。dare 源于原始印欧语词根 *deh₃-（给），因此 add 的本质即为“给予”^[10]。通过添加动名词后缀 -nd，得到 addend（加数，意为“待给予之物”）。类似地，由 augere（增加）派生出 augend（被加数，意为“待增加之物”）。中古英语术语 adden 和 adding 则由乔叟推广。^[11]

级数的和可以用求和符号（summation）表示，属于迭代的一种。例如：

${\displaystyle \sum _{k=1}^{5}k^{2}=1^{2}+2^{2}+3^{2}+4^{2}+5^{2}=55}$

至于 summand 和 sum ，则源自拉丁语名词 summa（意为“最高者”或“顶端”）和相关联的动词summare。此用法承袭自古希腊与古罗马将总和置于列顶的书写传统：在做加法时，这里的人通常将结果写在加数的上面，因此和字面上就比加数要“高”，^[12]这与现代的写法恰恰相反。

性质

交换律

用方块展示 4 + 2 = 2 + 4

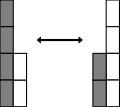
加法满足交换律：左右两个加数的顺序可以调换，结果不变。用符号语言来说，设 a 与 b 为任意两个数，则 a + b = b + a。

有一些其他的二元运算也满足交换律，例如乘法^[13]，但不是所有二元运算都满足交换律，例如减法和除法^[14]就不满足交换律。

结合律

利用分段的绳子展示的 2 + (1 + 3) = (2 + 1) + 3

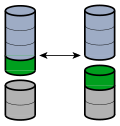
加法满足结合律：多个数相加，运算顺序可以调换，结果不变。设 a、b、c 为任意三个数，则 (a + b) + c = a + (b + c) 。例如，当 a = 1，b = 2，c = 3 时： ${\displaystyle (1+2)+3=3+3=6=1+5=1+(2+3)}$

然而，当加法与其他运算共同使用时，运算顺序就变得至关重要。在标准运算顺序中，加法的优先级低于乘方、${\displaystyle n}$ 次方根、乘法和除法，但与减法具有同等优先级。^[15]

单位元

用装有点的包展示 5 + 0 = 5

任何数加 0 都等于其本身；零是加法单位元。设 a 为任意数，则 a + 0 = 0 + a = a 。这个性质最早在婆罗摩笈多的《婆罗摩历算书》（公元628年）被提及，尽管他根据 a 是正数、负数还是零分成了三种情况，并且使用文字说明，而不是代数符号。之后的印度数学家们将这三种情况精简成了一种情况。大约 830 年，印度数学家 Mahavira 写道：“零加上一个数就会变成那个数”，对应一元陈述 0 + a = a 。12 世纪时，印度数学家婆什迦罗写道：“任何一个量（正负均可），加零或减零后保持不变”，对应一元陈述 a + 0 = a 。

后继

主条目：后继函数

在整数中，加数为 1 的加法有特殊意义：对于任何整数 a，整数 (a + 1) 是大于 a 的最小整数，称为 a 的后继。例如，3 是 2 的后继，7 是 6 的后继。这样，a + b 可以视为 a 的第 b 个后继，加法成为后继函数的迭代函数。例如，8 是 7 的后继，7 是 6 的后继，所以 8 是 6 的第 2 个后继，因此 6 + 2 = 8 。

单位

将有单位的物理量相加时，只有相同单位的量可以相加。例如，50 毫米加 150 毫米等于 200 毫米。相加不同的量时，情况则不同，例如5 英尺加 2 英寸等于 62 英寸，因为 1 英尺等于 12 英寸。另一个例子是，3 米加 4 平方米没有意义，因为米和平方米没有可比性。这是因次分析的一个基本例子。

不同的加法运算

有许多二元操作可以被视为实数加法的扩展。抽象代数主要关心这类扩展，集合论与范畴论中也有它们的影子。

自然数加法

更多信息：自然数

目前有两种流行的方法用于定义两个自然数 a 和 b 的和。如果自然数被定义为有限集合的元素个数，那么 a + b 可以这样定义：设 N(S) 为集合 S 中的元素个数。设 A 与 B 为不相交的集合且 N(A) = a 且 N(B) = b。那么 a + b 定义为 N(A ∪ B)（A ∪ B 表示 A 和 B 的交集）。另一种方法是允许 A 与 B 相交并取它们的不交并集（一种允许公共的元素被分开计算两次的运算）。

另一种流行的方法是递归：设 n⁺ 为 n 的后继，即继 n 后的下一个自然数，因此 0⁺ = 1，1⁺ = 2，依此类推。定义 a + 0 = a，并通过 a + (b⁺) = (a + b)⁺ 递归地定义一般的加法。因此 1 + 1 = 1 + 0⁺ = (1 + 0)⁺ = 1⁺ = 2。同样，这种定义也有很多变种。上述定义实际上是递归定理在部分有序集 N² 上的一个应用。然而，一些文献倾向于使用只在自然数集合上有定义的狭义递归定理：先将 a 临时想象为固定的，在 b 上应用递归以定义一元函数“ f(b) = a + b ”，然后将这些一元函数组合在一起形成完整的二元运算。早在 1854 年，德国数学家理查德·戴德金就发展了这种递归定义，并在接下来的几十年中扩展了这个定义。他利用数学归纳法证明了交换律、结合律等性质。

整数加法

更多信息：整数

整数最简单的理解就是由绝对值（一个自然数）和符号（一般情况下，正或负）组成。整数零是一个特殊情况：它既不是正数也不是负数。对于任何整数 n，定义 |n| 为 n 的绝对值。设 a 与 b 为整数，则它们的和 a + b 的定义需要分类讨论：

• 如果 a = 0，那么 a + b = b；如果 b = 0，那么 a + b = a。例如：(−2) + 0 = −2。特别地，0 + 0 = 0。
• 如果 a 和 b 都是正数，那么 a + b = |a| + |b|。例如：4 + 1 = 5。
• 如果 a 和 b 都是负数，那么 a + b = −(|a| + |b|)。例如：(−4) + (−1) = −(|−4| + |−1|) = −(4 + 1) = −5。
• 如果 a 和 b 一正一负，那么 a + b 的绝对值等于 a 的绝对值和 b 的绝对值之差（即 ||a| − |b||），符号与 a 和 b 中绝对值较大的一项符号一致。例如：(−6) + 4 = −2，因为 −6 和 4 一正一负，所以 (−6) + 4 的绝对值等于它们的绝对值之差 |−6| − |4| = 2，又因为负数项 −6 的绝对值大于正数项 4 的绝对值，结果为负，因此结果为 −2。

尽管对于实际的问题来说，这个定义足够了，但对于优雅的一般性的数学证明来说，它实在是太复杂了，情况太多了。

一个数学上更方便的整数的理解方式是使用格罗滕迪克群构造。给定自然数及其加法运算（+）和单位元 0 的定义，每个整数都可以（不唯一地）表达为两个自然数 a 和 b 的（未正式定义的）差，因此可以将整数定义为两个自然数组成的数对(a, b)。将等价的数对（差相同）考虑为同一个整数是个小问题。两个这样的新的整数 (a, b) 与 (c, d)（其中 a、b、c、d 为整数）的和（用 ⊕ 符号表示）通过自然数的加法（+）定义为：

只用整数的加法定义的 (−2) + 1：(2 − 4) + (3 − 2) = 5 − 6。

${\displaystyle (a,b)\oplus (c,d)=(a+c,b+d)}$

规定整数的加法单位元由数对 (a, a) 生成，且 (a, b) 的加法逆元由 (b, a) 生成（即 −(a, b) = (b, a)），这样整数的加法群的说明就完整了。利用加法逆元定义负数，将减法定义为“加加法逆元”，都比单独构造一个减法运算（在基础数学中被认为是逆运算）要方便许多。

分数加法

分数的加法可以用最小公分母计算，但从概念上来说只要用加法和乘法就可以了：

${\displaystyle {\frac {a}{b}}+{\frac {c}{d}}={ad+bc \over bd}}$

例如，${\displaystyle {\textstyle {\frac {3}{4}}+{\frac {1}{8}}={3\times 8+4\times 1 \over 4\times 8}={24+4 \over 32}={\frac {28}{32}}={\frac {7}{8}}}}$。

当分母相同时，分数的加法就更简单了，只要将分子相加，分母不变就行了：

${\displaystyle {\frac {a}{c}}+{\frac {b}{c}}={\frac {a+b}{c}}}$

例如，${\displaystyle {\textstyle {\frac {1}{4}}+{\frac {2}{4}}={\frac {1+2}{4}}={\frac {3}{4}}}}$。

有理数加法的交换律和结合律可以由整数算术的性质很容易地推导而来，见分式环。

实数加法

更多信息：实数的构造

复数加法

复数加法的视觉化表示。图中 O 为原点（0），向量 A（红色）与 B（蓝色）表示复数加数，X 是结果 A + B 所在的点。

要将两个复数相加，只需将实数部分和虚数部分分别相加即可，即：

${\displaystyle (a+bi)+(c+di)=(a+c)+(b+d)i}$

利用复数在复平面上的视觉化表示，复数的加法可以几何解释为：两个复数 A 和 B（解释为复平面上的点）的和，是由以 A、B 与原点 O 为顶点的平行四边形得到的顶点 X（如图所示）。等价地说，X 是使三角形 OAB 与三角形 XBA 全等的点。

抽象代数加法

向量加法

更多信息：向量

在线性代数中，向量空间是一个允许向量相加及缩放的代数结构。所有实数的有序对组成的集合就是一个常见的向量空间：有序对 (a, b) 被解释为欧几里得平面上从原点到由 (a, b) 表示的点的向量。两个向量的和是通过将对应的坐标相加完成的：(a, b) + (c, d) = (a + c, b + d)。

在经典力学中，向量解释为力，因此这个加法运算是经典力学的基础。

矩阵加法

更多信息：矩阵

大小相同的两个矩阵可以相加。两个 m × n 矩阵 A 和 B 的和也是一个 m × n 矩阵，用 A + B 表示，由对应元素相加得到：

${\displaystyle {\begin{aligned}\mathbf {A} +\mathbf {B} &={\begin{bmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\\\end{bmatrix}}+{\begin{bmatrix}b_{11}&b_{12}&\cdots &b_{1n}\\b_{21}&b_{22}&\cdots &b_{2n}\\\vdots &\vdots &\ddots &\vdots \\b_{m1}&b_{m2}&\cdots &b_{mn}\\\end{bmatrix}}\\&={\begin{bmatrix}a_{11}+b_{11}&a_{12}+b_{12}&\cdots &a_{1n}+b_{1n}\\a_{21}+b_{21}&a_{22}+b_{22}&\cdots &a_{2n}+b_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}+b_{m1}&a_{m2}+b_{m2}&\cdots &a_{mn}+b_{mn}\\\end{bmatrix}}\end{aligned}}}$

例如：

${\displaystyle {\begin{bmatrix}1&3\\1&0\\1&2\end{bmatrix}}+{\begin{bmatrix}0&0\\7&5\\2&1\end{bmatrix}}={\begin{bmatrix}1+0&3+0\\1+7&0+5\\1+2&2+1\end{bmatrix}}={\begin{bmatrix}1&3\\8&5\\3&3\end{bmatrix}}}$

模算数加法

更多信息：模算数

集合论与范畴论中的加法

自然数加法的一个影响深远的扩展即是集合论中的序数和基数的加法，它们是将自然数加法扩展到超限数的两种不同方式。不同于多数加法运算的是，序数的加法不满足交换律。不过，基数的加法满足交换律，且与不交并操作有着紧密的联系。

在范畴论当中，不交并操作是余积操作的一个特例。一般性的余积操作很可能是加法的所有扩展当中最抽象的一种。一些余积操作的命名突出了它们与加法运算的联系，例如直和和楔和。

发散级数加法

在通常意义下，发散级数没有传统意义上的“和”，但可以通过某些定义来求出该定义下发散级数的“和”，如切萨罗求和、阿贝尔求和、欧拉求和（英语：Euler Summation）等。这种扩展意义上的“和”不应与传统意义上的“和”混淆。

二进制加法

其他进位制下的加法和十进制加法很像。以二进制下的加法为例。两个二进制个位数相加相对来说比较简单，涉及到一种进位：

0 + 0 → 0

0 + 1 → 1

1 + 0 → 1

1 + 1 → 0，进位为 1（因为 1 + 1 = 2 = 0 + (1 × 2¹)）

两个“1”位相加得到“0”位并向前进位“1”。这和十进制下的加法很像：如果某一位的结果达到或超过基数 10，前一位需要加 1：

5 + 5 → 0，进位为 1（因为 5 + 5 = 10 = 0 + (1 × 10¹)）

7 + 9 → 6，进位为 1（因为 7 + 9 = 16 = 6 + (1 × 10¹)）

二进制的加法是一样的道理：二进制下的 1101 + 10111 = 100100（即十进制下的 13 + 23 = 36）如图所示。

竖式计算二进制加法 1101 + 10111 = 100100，即十进制下的 13 + 23 = 36。

运算方法

先天能力

自20世纪80年代起，关于数学发展的研究开始利用习惯化（英语：Habituation）现象​​：婴儿对意外情境的注视时间更长。^[16] 凯伦·温1992年的一项开创性实验通过屏风后操控米老鼠玩偶发现，5个月大的婴儿预期 ${\displaystyle 1+1=2}$ ，当实际情境暗示 ${\displaystyle 1+1}$ 等于 ${\displaystyle 1}$ 或 ${\displaystyle 3}$ 时，他们会表现出相对更强的惊讶反应。这一发现后来被采用不同研究方法的多个实验室反复验证。^[17]另一项1992年的实验，则针对18至35个月大的较大幼儿，通过让他们从盒中取出乒乓球来测试其运动控制能力的发展：年龄最小的幼儿能准确处理小数字，而年龄较大的受试者则能计算不超过5的数字之和。^[18]

此外，部分非人动物（特别是灵长类动物）也展现出有限的加法能力。^[19][20]

从数数开始学加法

通常，儿童最先掌握的是数数能力。当遇到需要将多个物品组合的问题时，年幼的孩子会借助实物（通常是手指或图画）来模拟情境，然后数出总数。随着经验的积累，他们逐渐学会或发现“接着数”的策略：当被要求计算 ${\displaystyle 2+3}$ 时，孩子会从 ${\displaystyle 2}$ 开始接着数三个数，即“${\displaystyle 3}$、${\displaystyle 4}$、${\displaystyle 5}$”（通常会逐根屈指计数），最终得出 ${\displaystyle 5}$ 这个结果。这种策略几乎具有普适性，孩子们很容易从同伴或老师那里习得。^[21]大多数孩子也能独立发现这一方法。

不同的国家在不同的年龄教授整数和算术。许多国家在学前就教授加法。然而，世界上几乎所有国家都在小学一年级结束前教授加法。

一位数的运算法

在十进制体系中，要进行任意数的加法运算，其前提是具备两位一位数（ ${\displaystyle 0}$ 到 ${\displaystyle 9}$ 之间的数）相加的能力。由于参与相加的两个一位数各有10种选择，所以总共会有100个一位数“加法算式”，这些算式可以用加法表呈现出来。

+	0	1	2	3	4	5	6	7	8	9
0	0	1	2	3	4	5	6	7	8	9
1	1	2	3	4	5	6	7	8	9	10
2	2	3	4	5	6	7	8	9	10	11
3	3	4	5	6	7	8	9	10	11	12
4	4	5	6	7	8	9	10	11	12	13
5	5	6	7	8	9	10	11	12	13	14
6	6	7	8	9	10	11	12	13	14	15
7	7	8	9	10	11	12	13	14	15	16
8	8	9	10	11	12	13	14	15	16	17
9	9	10	11	12	13	14	15	16	17	18

熟练且准确地计算一位数加法是早期算术学习的主要重点。有时，教师会鼓励学生通过死记硬背的方式记住完整的加法表，但基于规律的策略通常更具启发性，而且对大多数人来说效率更高：^[22]

• 利用交换律：这一规律能把需要掌握的算式数量从 100 个降低到 55 个。
• 加 ${\displaystyle 1}$ 或加 ${\displaystyle 2}$ ：这是一种基本运算，既可以通过接着数的方法来完成，最终也能凭借直觉快速得出结果。
• 加 ${\displaystyle 0}$ ：${\displaystyle 0}$ 是加法单位元，所以加 ${\displaystyle 0}$ 的运算很简单。不过，在算术教学中，有些学生最初接触加法时，会认为加法运算总会使加数增大。此时，一些应用题可以帮助他们理解加 ${\displaystyle 0}$ 这个“例外情况”。
• 相同数相加：一个数与自身相加，这与以及乘法运算相关联。相同数相加的算式是推导许多相关算式的基础，学生们通常觉得这类算式比较容易掌握。
• 近似相同数相加：类似 ${\displaystyle 6+7=13}$ 的算式，可以基于相同数相加的算式 ${\displaystyle 6+6=12}$ ，只需再加 ${\displaystyle 1}$ 得出结果；也可以从 ${\displaystyle 7+7=14}$ 出发，减 ${\displaystyle 1}$ 得到答案。
• 与 ${\displaystyle 5}$ 或 ${\displaystyle 10}$ 相加：形如 ${\displaystyle 5+x}$ 和 ${\displaystyle 10+x}$ 的算式通常会较早被记住，并且可以用来推导其他算式。例如， ${\displaystyle 6+7=13}$ 可以从 ${\displaystyle 5+7=12}$ 推导得出，只需再加 ${\displaystyle 1}$ 。
• 凑十法：这是一种“相对更高级的”策略。对于涉及 ${\displaystyle 8}$ 或 ${\displaystyle 9}$ 的加法运算，可以借 ${\displaystyle 10}$ 作中间数。例如， ${\displaystyle 8+6=8+2+4=10+4=14}$ 。

随着学生年龄增长，他们会记住更多算式，并学会快速、流畅地推导其他算式。许多学生不会记住所有的加法算式，但仍然能够快速算出任何基本的加法结果。

进位

竖式计算 ${\displaystyle 59+27=86}$

主条目：进位

多位数加法的标准算法是竖式计算：将加数竖直对齐，从最右侧的个位列开始，依据上述加法表逐列相加。若某一列相加结果超过九，则将超出部分的数字（即"进位"）传递至下一列。例如图中计算 ${\displaystyle 59+27}$ 时，个位列的运算为 ${\displaystyle 9+7=16}$ ，其中数字 ${\displaystyle 1}$ 即为进位。

另一种计算策略是，从最左侧的最高位开始相加。此法会使进位操作稍显复杂，但能更快地得出总和的近似值。

带小数点的运算法

小数加法只需对上述多位数加法流程稍作调整即可实现。具体操作时，先将两个小数上下对齐，确保小数点位置一致。若遇到位数不等的情况，可在较短的小数末尾补零，使其与较长的小数具有相同的位数。随后，按照前述多位数加法的方法进行计算。唯一区别在于：最终答案中的小数点必须与加数中的小数点保持在同一垂直位置。^[23]

例如，计算 ${\displaystyle 45.1+4.34}$的过程如下：

   4 5 . 1 0
+  0 4 . 3 4
————————————
   4 9 . 4 4

${\displaystyle 4.34}$开头的 ${\displaystyle 0}$ 可不写。

科学记数法

主条目：科学记数法 § 基本计算

在科学记数法中，一个数以 ${\displaystyle x=a\times 10^{n}}$ 的形式表示，其中 ${\displaystyle n}$ 是整数且 1 ≤ a < 10。为了将两个以科学记数法表示的数相加，它们的指数部分必须相同。^[24]例如：

${\displaystyle 2.34\times 10^{-5}+5.67\times 10^{-6}=2.34\times 10^{-5}+0.567\times 10^{-5}=2.907\times 10^{-5}}$

计算机算法

模拟计算机算加法

用运算放大器（op-amp）算加法。详见求和放大器（英语：Operational amplifier applications#Summing amplifier）。

模拟计算机直接处理物理量，因此其加法机制取决于加数的形式。机械式加法器可能将两个加数表示为滑块的相对位置，这种情况下可以通过平均杠杆来实现加法。如果加数是两个轴的转速，则可通过差速器来实现加法。液压式加法器可以利用牛顿第二定律，通过平衡活塞组上的力来计算两个腔室中的压强之和。

对通用模拟计算机而言，最常见的情况是计算两个（以地为参考的）电压之和，这可以通过电阻网络粗略实现，但更好的设计是利用运算放大器来实现。^[25]

数字计算机算加法

加法同时也是数字计算机运行的基础，其中加法效率（尤其是进位机制）是影响整体性能的重要限制因素。^[26]

传统数字计算机

参见：算盘和差分机

提到传统数字计算机，算盘是其代表。在现代书面数字系统出现前，算盘就已沿用了几世纪，其历史至少可追溯到公元前2700–2300年的苏美尔。^[27]

1642年，帕斯卡发明了机械计算器；^[28]它是第一台可运行的加法机（英语：Adding Machine）。帕斯卡计算器受限于其依靠重力辅助的进位机制，其轮子只能单向转动。要进行减法运算，操作员必须使用帕斯卡计算器的补码，而这所需的步骤和加法一样多。^[29]

1694年，莱布尼茨制造出了另一种机械计算器——步进计算器（英语：Stepped reckoner）。1709年，乔瓦尼·波莱尼（英语：Giovanni Poleni）对其设计进行了改进，制造出了一台由木材制成的计算钟，能够执行所有四则运算。

这些早期尝试并未取得商业成功，但为19世纪后期的机械计算器提供了灵感。^[30]

差分机的部分结构

电子数字计算机

全加器逻辑电路，将两个二进制数字A和B与进位输入C_in相加，产生和位S和进位输出C_out。

在电子数字计算机中，加法器负责执行整数加法，通常采用二进制算术（英语：Binary_number#Binary_arithmetic）。最简单的架构是行波进位加法器，它遵循标准的多位数加法算法。一种稍作改进的设计是进位跳过架构，同样符合人类的直觉：在计算 ${\displaystyle 999+1}$时，人们不会执行所有的进位操作，而是跳过连续的 ${\displaystyle 9}$ ，直接得出结果。^[31]

实际上，计算加法可以通过异或和与位逻辑运算结合位移操作来实现。异或门和与门在数字逻辑中易于实现，从而可以构建全加器电路，这些电路又可以组合成更复杂的逻辑运算。在现代数字计算机中，整数加法通常是速度最快的算术指令，但它对性能的影响最大，因为所有浮点运算以及诸如内存访问期间的地址生成和分支期间的指令获取等基本任务都依赖于它。为了提高速度，现代设计采用并行计算数字的方法；这些方案被称为进位选择、进位预测和Ling（英语：Ling adder）伪进位等。实际上，许多实现都是这最后三种设计的混合体。^[32]

20世纪50年代末和60年代初的一些十进制计算机使用加法表而非加法器，例如RCA 301^[33]和IBM 1620（英语：IBM 1620）^[34]。

计算机浮点数

主条目：浮点数运算

计算机还有另一种表示数字的方法，称为浮点数运算，它类似于上文所述的科学记数法，有助于缓解溢出问题。每个浮点数由两部分组成：指数和尾数。要相加两个浮点数，其指数必须对齐，这通常意味着需要对较小数字的尾数进行移位。如果较大数与较小数之间的差距过大，可能会导致精度损失。如果要向一个大数累加许多较小的数，最好先将这些较小的数相加，再将总和与大数相加，而不是逐个将小数累加大数。这使得浮点加法通常不具备结合律。^[35]

相关运算

加、减、乘、除是基础算术中的基本运算。

算术

减法可以视为一种特殊的加法——减一个数等于加它的加法逆元。减法本身就是加法的一种逆运算，因为加 x 和减 x 互为反函数。给定一个定义有加法运算的集合，不总能够定义一个对应的减法运算，自然数的集合就是一个很简单的例子。然而，反过来说，一个减法运算唯一地确定一个加法运算、一个加法逆元运算、一个加法单位元。因此，一个加法群可以描述为一个在减法运算下封闭的集合。

乘法可以想成是重复的加法。如果一个单项 x 在加法运算中出现 n 次，那么这个加法运算的结果就是 x 和 n 的积。即使 n 不是自然数，这个积仍然可能是有意义的，例如当 n = −1 时，这个积就是 x 的加法逆元。

在实数和复数域中，加法和乘法可以通过指数函数互相交换：

${\displaystyle \mathrm {e} ^{a+b}=\mathrm {e} ^{a}\cdot \mathrm {e} ^{b}}$

这个恒等式允许借助对数表并手动计算加法完成乘法，也使得计算尺上可以进行乘法。在将无穷小量与李代数上的向量加法相互联系起来的李群的广义语境下，这个公式仍然能给出一个较好的第一近似。

一个圆形的计算尺

乘法的扩展甚至比加法更多。一般情况下，乘法对加法满足分配律，环的定义明确说明了这一要求。在有些语境下，例如整数，乘法对加法的分配律和乘法单位元的存在足以唯一确定乘法运算。分配律还给出了加法的一些信息，例如：将乘法算式 (1 + 1)(a + b) 用两种方法展开可以得到加法的交换律。因此，一般地，环的加法满足交换律。

除法和加法的联系相对来说没有那么紧密。因为 ${\displaystyle \textstyle {\frac {a}{b}}=a\cdot b^{-1}}$，所以除法对加法满足右分配律，即 ${\displaystyle \textstyle {a+b \over c}={\frac {a}{c}}+{\frac {b}{c}}}$（c ≠ 0），但不总是满足左分配律，例如 ${\displaystyle \textstyle {1 \over 2+2}={\frac {1}{4}}\neq 1={\frac {1}{2}}+{\frac {1}{2}}}$。

最大值操作

最大值操作 max(a, b) 作为一个二元运算，与加法很相似。事实上，如果两个非负整数 a 和 b 不是一个数量级的，那么它们的和与它们的最大值将会很接近。这个近似在数学应用中极其有用，例如在截断泰勒级数的时候。然而，在数值分析中它是一个经常出现的令人头疼的问题，其根本原因是最大值操作是不可逆的。如果 b 远大于 a，那么 (a + b) − b 直觉化的计算会导致不可接受的舍入误差，甚至得到结果 0。（参见精度丢失）

在无穷极限中，这个近似变得精确：如果 a 和 b 中有一个是无穷基数，那么它们的基数和等于它们之中较大者。相应地，无穷基数不可相减。

和加法一样，最大值操作满足交换律和结合律。更进一步，由于加法保持了实数的序，加法对最大值操作满足分配律，就像乘法对加法满足分配律那样：

${\displaystyle a+\max(b,c)=\max(a+b,a+c)}$

因此，在热带几何中，乘法由加法代替，加法由最大值操作代替。在这个语境下，加法称作“热带乘法”，最大值操作称作“热带加法”，“热带加法单位元”是 −∞。不过，有些作者倾向于使用最小值操作来代替加法，这样“加法单位元”就是 +∞。

将这些结论放在一起，可以得到：热带加法通过对数近似于一般的加法：

${\displaystyle \log _{k}(a+b)\approx \max(\log _{k}a,\log _{k}b)}$

当底数 k 增加，这个近似变得越来越精确。提出一个常数 h（与量子力学中的普朗克常数类似命名）并取 h 趋向 0 时的经典极限，这个近似就可以变得精确：

${\displaystyle \max(a,b)=\lim _{h\to 0}h\log(\mathrm {e} ^{a/h}+\mathrm {e} ^{b/h})}$

在这种意义下，最大值操作实质上是加法的“解量化”版本。

其他方式的加法

自增操作，又叫后继，是加 1 的操作。

求和符号（${\displaystyle \textstyle \sum }$）表述了任意多个数（通常不止两个）的加法。它涵盖了一个数的和（即其自身）和空和（即 0）。无穷加和即级数，是一个十分脆弱且易错的过程。

有限集合的计数等价于在这个集合上将 1 相加。

积分是在连续统上的“加法”；更精确且更具一般性地说，是在一个可导流形上的“加和”。零维流形上的积分即是加和。

线性组合是每项都有一个系数（通常是实数或复数）的加和，它结合了乘法和加法。线性组合在直觉化的加法将会违反一些规范化规则的场合下尤其有用，例如游戏理论中的混合策略及量子力学中的量子态的态叠加。

卷积是由概率分布函数定义的随机变量的加法。它的通常的定义涉及到积分、减法和乘法。一般地，卷积作为一种定义域加法发挥作用，而向量加法则是一种值域加法。