热门问题
时间线
聊天
视角
升力
来自维基百科,自由的百科全书
Remove ads
升力(英语:Lift)。当流体流经一个物体的表面时会对其产生一个表面力,而则这个力垂直于流体流向的分力即为升力[1],与之相对的则是平行于流体流向的阻力。如果流体是空气时,它产生的升力便叫做空气动力。航空器要想升到空中,必须能产生能克服自身重力的升力[2]。

升力主要是靠机翼对空气取得,飞机的翼形断面形状有很多种类,依照每种形状适用于不同功用的飞机,飞机的机翼从断面来看,通常机翼上半部曲面及下半部曲面不一样,通常为上半部曲面弧长较长,空气流经飞机的机翼截面,因空气流过机翼表面时被一分为二,经过机翼上表面的空气是沿着曲线运动的(因为机翼上表面是弯曲的),所以会产生负压(负压提供空气沿曲线运动所需的向心力),而经过机翼下面的空气是沿着比较平缓的表面运动的(机翼下表面相对平直),所以不会产生负压(参见简化的物理解释),机翼下部压力高,上部压力小,压力高的地方会往压力低的部分移动,这就是升力的由来。[3]
Remove ads
解释
升力取决于空气的密度,速度的平方,空气的黏性以及空气的可压缩性,空气流经物体的表面积,物体的形状,以及物体与气流的夹角。一般来说,升力与物体外形,气流夹角,空气的黏性,以及空气的可压缩性这几项的关联是非常复杂的。
升力,就是向上的力。从翼形流线谱中看出:相对气流稳定而连续地流过翼形时,上下表面的流线情况不同。上表面流线是弯曲的,其气会产生负压、因此压力小;而下表面流线较平直的,其气流不会产生负压,压力较大。因此,产生了上下压力差。这个压力差就是空气动力(R),它垂直流速方向的分力就是升力(Y)。流过各个剖面升力总合就是机翼的升力。升力维持飞机在空中飞行。
翼形升力的简化物理解释

翼形是流线型的,能够产生比阻力大得多的升力[4]。平板可以产生升力,但其升力不如流线型翼形来得大,阻力也略高。
有几种方法可以解释翼形如何产生升力。某些方法较为严格复杂,有些则是错的[5][6][7][8][9]。例如,基于牛顿运动定律的解释和基于伯努利原理的解释皆可以解释升力[10][11]。

气流经过翼形时,翼形会对空气施加向下的力,根据牛顿第三定律,空气必须对翼形施加大小相等、方向相反的反作用力,也就是方向朝上的升力[12][13][14][15]。
气流在经过翼形时改变方向,沿著向下弯曲的路径流动。根据牛顿第二定律,这种流动方向的改变,需要翼形对空气施加向下的力。牛顿第三定律则要求空气对翼形施加向上的力;因此产生了与方向变化相反的反作用力——升力。就飞机机翼的情况而言,机翼对空气施加向下的力,空气对机翼施加向上的力。[16][17][18][19][20][21]
气流之所以向下偏转,并非仅仅由翼形的下表面造成,翼形上方的气流也占了很大的因素。
伯努利原理指出,流体的压力和速度之间存在著直接的数学关系,因此,如果知道气流中每一点的速度,就可以计算出压力,反之亦然[22]。对于任何产生升力的翼形,必然存在压力不平衡,即顶部的平均气压低于底部。伯努利原理指出,这种压力差必须伴随著速度差。

由理论和实验中观察到的流动型态,上表面流速增加的原因,可以用流管夹紧和质量守恒来解释[23]。
对于不可压缩流,质量不会被创造或破坏,所以当流管变窄时,为了保持流量恒定,在每个流管内,体积流率(例如每分钟的体积单位)必须保持恒定,变窄区域内会增加流速,以满足质量守恒原理[24]。
在翼形的情形,因为向上流动和围绕翼形,所以上部流管收缩。由于质量守恒,流速必须随著流管面积的减小而增大。同样,下部流管会膨胀,导致流速变慢[23]。
根据伯努利原理,上表面流速较快,因此上表面压力小于流速较慢的下表面压力。这种压力差产生了向上的净空气动力。
产生升力需要维持垂直和水平方向上的压力差,故同时需要“气流的向下偏转”以及“符合伯努利原理的流速变化”。因此上述的简化解释不够完整,因为它们只根据其中一项来定义升力。根据细节,简化的解释还有其他缺陷。
基于流体偏转和牛顿定律的解释是正确的,但仍不完整。它并没有解释,翼形如何使比它实际碰触部分还远得多的流体也能产生偏转。此外,它也没有解释水平方向上的压力差是如何维持的。也就是说,它忽略了相互作用中“伯努利原理所影响的部分”[25]。
而伯努利原理的解释,建立在上表面有更高的流速,但未能正确解释是什么导致了流速加快:
- 质量守恒的解释建立于上表面流管会变窄,但这并不能解释为什么流管会改变尺寸。要知道为什么空气会这样流动需要更复杂的分析[26][27][28]。
- 有时,人们会提出一个几何参数来说明为什么流管的尺寸会发生变化:有人断言,与底部相比,顶部“阻碍”或“压缩”空气的程度更大,因此流管更窄。对于底部平、顶部弯的传统翼形情形,这感觉是直观的。但它并未解释平板、对称翼形、帆船帆布或倒飞的传统翼形是如何产生升力的,基于收缩量计算升力的尝试也无法预测实验结果[29][30][31][32]。
- 常见的等过境时间版本是错误的,解释见下文。
只考虑伯努利的解释意味著,速度差是由压力差以外的原因所引起,且根据伯努利原理,速度差会再导致压力差,但是这种隐含的单向因果关系是一种误解,压力和速度之间真正的因果关系是相互的。最后,只有伯努利的解释不能解释垂直方向上的压力差是如何维持的。也就是说,它们忽略了相互作用中向下偏转气流的部分[25]。
Remove ads
对于翼形升力的产生,人们提出了许多不同的解释,大多数是为了向大众解释升力现象。虽然这些解释可能与上述解释有共通点,但可能会引入额外的假设和简化。有一些解释引入了被证明是错误的假设,如“相同过境时间假设”。一些则是使用了有争议的术语,如“康达效应”。
在基础或常见的资料中,“等过境时间”理论经常用于描述升力,该理论错误地认为,在翼形前缘分离的气团必须在后缘重新汇合,迫使沿较长上表面飞行的空气速度更快。然后引用伯努利原理得出结论,沿著机翼底部移动的气流速度较慢,气压一定会更高,从而推动机翼上升[33]。
然而,没有物理原理要求等过境时间这个条件成立,实验结果则表明该假设是错误的[34][35][36][37][38][39]。事实上,翼形上方产生升力的空气运动速度比等过境理论预测的要快得多[40]。此外,这个理论也违反了牛顿第三运动定律,因为它描述了作用在机翼上的力,却没描述反作用力[41]。
空气必须同时到达后缘的论断有时被称为“等时间谬论”[42][43][44][45][46]。

起初,康达效应指的是,流体射流会维持“附著在偏离流体的相邻弯曲表面”的趋势,由此将环境空气卷入流体。 这种效应命名自罗马尼亚的空气动力学家康达(Henri Coandă),他在多项专利中充分应用了该效应。
概括地说,一些人认为,这种效应包括了任何“流体边界层会去附著在曲面上”的趋势,而不只是专用于流体射流的边界层。在这个更广泛的意义上,某些人用康达效应解释为何气流会维持在翼形上的附著状态[47]。例如,Jef Raskin[48]描述了一个简单的演示,他以一根吸管吹气,使气流通过轻木机翼的上表面,机翼因此向上偏转,从而证明康达效应能够产生升力。这个演示以流体喷射(吸管所排放的气流)紧临曲面(机翼),正确展示了康达效应。然而,上表面的气流是一个复杂的、充满涡流的混合层,而与此同时,下表面的气流却是静止的。因此,这个演示的物理性质与一般通过机翼上方的气流有很大的不同[49]。这种用法在一些流行的空气动力学参考文献中也曾出现过[47][48],而这是对“康达效应”充满争议的用法。更公认的空气动力学领域观点是,康达效应被定义在比上述更受限的意义上[49][50][51],沿著上表面的气流只是反映出“缺乏了边界层的分离”; 因此它不是康达效应的一个例子[52][53][54][55]。
基本的升力因素
压力是单位面积上由空气施加在自身和它所接触的表面上的正向力。升力是透过垂直于翼型表面的压力传递的。因此,合力以压力差的方式呈现,合力方向意味著翼型上表面的平均压力低于下表面的平均压力。[56]这些压力差与弯曲气流一起出现。当流体沿曲线路径流动时,存在垂直于流动方向的压力梯度,曲线外侧压力较高,内侧压力较低。[57]这种弯曲流线和压力差之间的直接关系,有时称为流线曲率定理,是莱昂哈德·欧拉于1754年从牛顿第二定律推导出:
该方程的左侧表示垂直于流体流动的压力差。右侧ρ是密度,v是速度,R是曲率半径。该公式表明,较高的速度和更紧密的曲率会产生较大的压力差,且直线流动(R→∞)压力差为零。[58]
Remove ads

攻角是指翼形的弦线与迎面气流之间的角度。对称翼形在攻角为零时不会产生升力。但随著攻角的增加,偏转空气通过更大的角度,增加了气流速度的垂直分量,从而产生更大的升力。在小角度的情况下,对称翼形产生的升力与攻角大致成正比[59][60]。
随著攻角的增加,升力将在某个角度达到最大;攻角增加至超过此临界攻角会导致上表面的气流与机翼分离;向下偏转的气流变少,因此翼形产生的升力也变小,称为失速。[61]

在给定的空速下,翼形所能产生的最大升力取决于翼形的形状,特别是弧度大小(使上表面比下表面更凸的曲率,如右图所示)。增加弧度通常会提升特定空速下的最大升力。[62][63]
有弧度翼形在零攻角时会产生升力。当弦线(chord line)呈水平时,后缘的方向向下,空气沿后缘流动而向下偏转。[64]当有弧度翼形被上下颠倒时,可调整攻角使升力向上。这就解释了为什么飞机可以倒飞[65][66]。
影响升力的环境流动条件包括流体密度、黏度和流动速度。密度受温度和介质声速的影响,即受可压缩性影响。
升力与空气密度成正比,大约与流速平方成正比。升力还取决于机翼大小,一般与机翼在升力方向的投影面积成正比。升力以基于这些因子的升力系数来量化,在计算上很方便。
无论翼形的表面看起来多么光滑,在空气分子的尺度上任何表面都是粗糙的。飞入表面的空气分子会从粗糙的表面反弹,并相对于其原来的速度随机反弹至不同方向。其结果是,当空气被看作是一种连续性材料时,它被视为无法沿表面滑动,空气相对于翼形的速度在表面降至几乎为零(即空气分子被“黏”在表面上,不会沿著表面滑动),被称作不滑移条件(No-slip condition)。[67]由于表面的空气速度接近零,远离表面的空气却在移动,因此存在一个薄薄的边界层,边界层靠近表面的空气受到剪切运动的影响。[68][69]空气的黏性阻滞了剪力作用,在翼形表面产生了一个剪应力,称为表面摩擦阻力( skin friction drag)。在大多数翼型的大部分表面上,边界层都属于自然湍流,这增加了表面摩擦阻力。[69][70]
在通常的飞行条件下,边界层会同时维持附著在上表面和下表面,直到后缘,它对其他流动的影响不大。与不存在边界层的无黏性流理论的预测相比,附著的边界层适度减少了升力,并在一定程度上改变了压力分布,这导致了除表面摩擦阻力之外还出现了与黏度有关的压阻力(pressure drag)。表面摩擦阻力和与黏性有关的压阻力的总和通常被称为型阻(profile drag)。[70][71]

一个翼形在特定空速下的最大升力受到边界层分离的限制。随著攻角的增加至某程度,边界层无法持续附著在上表面。当边界层分离时,会在上表面留下一个循环流动的区域,如流动可视化的右图所示。这就是所谓的失速(stall或stalling)。升力在攻角大于失速点后会显著下降,但不会降至零。以升力系数表示,失速前的最大升力通常小于1.5,而采用大升力的开缝式襟翼(Slotted flap)和前缘装置的翼型则可以超过3.0 。[72]
钝体,又称非流线形体(bluff body)是一种非流线型不会发生失速的翼形,其周围的流动除了强大的阻力外,还可能产生升力。这种升力可能是稳定的,也可能会因涡旋泄离(Vortex shedding)而产生振荡。物体的弹性与涡旋泄离的相互作用可能会加强跳动升力(fluctuating lift)的效果,并引起流体涡旋诱发振动(vortex induced vibration, VIV)。[73]例如,围绕圆柱的流动会产生卡门涡街:涡流以交替的方式从圆柱的两侧脱落。流动的振荡性质在圆柱体上产生了一个跳动的升力,虽然净(平均)力可以忽略不计。此升力的频率以无因次的斯特劳哈尔数来描述,取决于流动的雷诺数[74][75]。
但对于弹性结构来说,这种振荡升力可能会引起流体涡旋诱发振动。在某些条件下(例如,共振或与翼展方向强相关的升力),由于升力跳动而产生的结构运动可能会被大幅加强。这种振动可能会带来问题,恐造成工业烟囱等高大人造结构的倒塌。[73]
在马格努斯效应中,旋转的圆柱体在自由流中产生升力。这里的机械性旋转作用于边界层,使其在圆柱体两侧的不同位置分离。 就流动而言,非对称分离改变了圆柱体的有效形状,使得圆柱体就像在外部流动中循环的升力翼型。[76]
更全面的物理解释
在“翼形升力的简化物理解释”中,有两种主要解释:一种是基于气流向下偏转(牛顿定律),另一种是基于压力差而伴随流速变化(伯努利原理)。这两种现像中的任何一种,都在一定程度上辨识了升力的面貌,但未解释其他重要部分。更全面的解释包括向下偏转和压力差(包括与压力差相关的流速变化),以及对气流更详细地研究[77]。
翼形形状和攻角共同作用,使翼形在气流经过时对空气施加向下的力。根据牛顿第三定律,空气必须对翼形施加一个大小相等、方向相反(向上)的力,也就是升力[14]。
当翼形表面出现压力差,空气会对翼形表面施加净力[78]。流体中的压力在绝对意义上总是正的[79],因此,必须把压力看作是推,而不是拉。因此,在翼形的任何地方,无论上表面或下表面,翼形会被压力往内推挤。为了对翼形的存在作出反应,气流通过时,会降低上表面压力以及增加下表面压力。因为向上推的下表面压力比向下推的上表面的压力来得大,最终的结果就是向上的升力[78]。
压力差直接造成作用于翼形表面的升力;然而,要理解压力差是如何产生的,就需要理解气流在更大范围内的作用[80]。

翼形在大范围内影响气流的速度和方向,产生一种称为速度场的模式。当翼形产生升力,翼形前面的流体向上偏转,而翼形上方和下方气流向下偏转,翼形后方的气流则再次向上偏转,远抛在后的气流与迎面而来的气流处于相同的状态。翼形上方的气流加快,而翼形下方的气流减慢。加上前面空气向上偏转和后面空气向下偏转,这就构成了气流的净循环分量。向下偏转及流速变化明显,并延伸到很远的区域,正如右边的气流动画所示。气流方向和速度上的差异在靠近翼形处最大,在远高于和低于翼形的地方逐渐减小。速度场的所有这些特征也在升力气流的理论模型中出现[81][82]。
压力也受到大面积的影响,形成一种称为压力场的非均匀压力模式。当翼形产生升力时,翼形上方有一个低压扩散区,翼形下方通常有一个高压扩散区,如图中的等压线(恒压曲线)所示。作用于表面的压力差只是这个压力场的一部分。

不均匀的压力,在压力由高到低的方向上,对空气施力。 在翼形周围的不同位置,如在等压线图中箭头方向所示,力的方向是不同的。 翼形上方的空气被推向低压区域中心,翼形下方的空气则被从高压区域中心向外推送。
根据牛顿第二定律,空气朝受力方向加速。因此,在等压线图中,垂直箭头指出,翼形上下方的空气被加速或向下偏转,因此,在气流动画中,非均匀压力可能是可见气流向下偏转的原因。为了产生这种向下转弯,翼形必须有一个正攻角,或是其后部向下弯曲,就像带有拱形的翼形。注意,上表面的气流向下翻转,是由于上面压力大于下面压力而将空气向下推的结果。有些解释(请参阅“康达效应”)表明,对于向下偏转,黏度将起到关键的作用,不过这是错误的解释。(请参阅“康达效应之争议”)。
翼形前方的箭头,表示前方的气流向上偏转;后方的箭头则表示,翼形后方的气流会在向下偏转后,再次向上偏转。这些偏移可以在气流动画中看到。
翼形前方和后方的箭头也表明,当空气通过翼形上方的低压区,会在进入时加速,离开时减速。空气通过翼形下方的高压区时,则是相反的情况——它先是减速,然后加速。因此,非均匀压力也是气流动画中流速变化的原因。而流速变化与伯努利原理一致,伯努利原理认为在无黏性的稳定流动中,压力小意味著速度快,而压力大意味著速度慢。
因此,流动方向和速度的变化是由非均匀压力直接引起的。但这种因果关系不仅是单向的,而是在两个方向上同时奏效。空气的运动受压力差的影响,但压力差的存在取决于空气的运动。因此,这种关系是一种互惠的相互作用:气流根据压力差改变速度或方向[83],而压力差是由空气对速度或方向变化的阻力维持的。只有当有东西可以推动时,压力差才会存在。在空气动力流动中,当空气因为压力差而加速时[84],压力差会推动空气的惯性。这就是为什么空气质量是计算的一部分,以及为什么升力取决于空气密度。
为了维持翼形表面升力所需的压力差,需要在翼形周遭的大范围内维持不均匀的压力模式。这就要求维持垂直和水平方向的压力差,既需要气流的向下偏转,也需要根据伯努利原理造成的流速变化。压力差与气流的方向和速度变化相互作用,相互支撑。压力差理所当然来自于牛顿第二定律,也来自于流体沿著翼形主要向下倾斜的轮廓流动这一事实。而空气具有质量这点,对相互作用也至关重要[85]。
产生升力既需要流体向下偏转,又需要与伯努利原理一致的流速变化。上述简化物理解释中给出的任一解释,只用其中一种方式来解释升力,因此只能解释现象的一部分,而未解释剩下的部分[25]。
量化升力
当翼形表面上的压力分布已知时,确定总升力需要将表面局部元素对压力的贡献加总,每个元素具有其自身的局部压力值。因此,总升力是垂直于远场流动方向的压力在翼形表面的积分。[86]
- S是翼形的投影(平面形状)面积,测量值与平均气流垂直;
- n是指向机翼的单位法向量;
- k是垂直于自由气流方向的单位向量。
升力取决于机翼的大小,大致与机翼面积成正比。通过量化升力系数给定机翼的升力通常很方便 ,它定义了机翼单位面积的整体升力[87]。
对于特定攻角的机翼,特定流量条件下产生的升力:
- L是升力
- ρ是空气密度
- v是速度或真实空速
- S是机翼的平面形状(投影)面积
- 是所需迎角、马赫数和雷诺数的升力系数
升力的数学理论
升力的数学理论建立在连续流体力学的基础上,该理论假设空气作为连续流体流动[88][89][90]。升力的成因是根据物理学的基本原理,其中最相关的有以下三条原理[91]:
- 动量守恒,这是牛顿运动定律的结果,尤其是牛顿第二定律,将空气中的合力和动量时变率联系起来。
- 质量守恒,包括翼形表面不被周围流动的空气所渗透的假设。
- 能量守恒,也就是说能量既不会被创造也不会被破坏。
因为翼形影响其周围广阔区域的流动,力学守恒定律以偏微分方程的形式体现,并结合一组边界条件,必须满足在翼形表面和远离翼形之条件[92]。
要预测升力,需要以计算流体动力学(CFD)方法,求解特定翼形形状和流动条件的方程,这通常需要大量的计算,只有在计算机上才有办法实现。当CFD要决定净空气动力时,会由CFD决定出在所有表面元素的压力及剪切力,并对其导致的力作“压力积分”。
纳维-斯托克斯方程(NS)提供了可能最精确的升力理论,但实际上,在翼形表面边界层,要掌握湍流的影响需要牺牲一定的精度,并且需要使用雷诺平均纳维-斯托克斯方程(RANS)。此外,也发展了其他更简单但不太准确的理论。
NS方程描述了质量守恒、牛顿第二定律(动量守恒)、能量守恒、用于黏度作用的牛顿定律、傅里叶热传导定律、与密度、温度和压力有关的状态方程,以及流体的黏度和导热系数的公式。[93][94]
NS方程结合翼型表面无通流(through-flow)和不滑移的边界条件,可用于以高精度预测平常任何在大气层内飞行的情况之升力。然而,实际情况下的气流总是涉及到边界层中的湍流,湍流会出现在机翼表面旁,至少在机翼的后部。
通过求解原始形式的NS方程来预测升力,需以计算来解决湍流的细节,甚至是最小的涡流。 即使在当前最强大的电脑上也尚无法做到。[95]因此,原则上NS方程提供了一个完整且非常精确的升力理论,但实际的升力预测需要将湍流效应在RANS方程中建立模型,而非直接计算。
RANS方程也是一组NS方程,但对湍流运动进行时间平均化,并考虑了湍流对以湍流模型表示的时间平均流的影响(湍流模型是一组附加方程组,基于因次分析并结合从平均时间的意义上来衡量湍流如何影响边界层的经验资讯)。[96][97]
RANS方程所需的计算量只是求解原始NS计算中所有湍流运动所需计算量的极小部分(十亿分之一)[94],随著大型计算机的出现,目前对完整的飞机进行三维RANS计算是可行的。由于湍流模型并不完美,RANS计算的精度也不完美,但对实际的飞机设计已足够。由RANS预测的升力通常在实际升力的百分之几以内。
欧拉方程是未考虑黏性、热传导和湍流效应的NS方程。[98]与RANS解相同,欧拉解由速度向量、压力、密度和温度组成,定义在翼型周围的密集网格点上。虽然欧拉方程比NS方程简单,但并不适合精确的解析解。
借由势流理论可再进一步简化,势流理论减少了待定未知数,使在某些情况下可能求得解析解,如下所述。
对于失速点以下的攻角,欧拉或势流的计算大致可正确预测翼型表面的压力分布,在失速点以下可能会漏掉10-20%的总升力。在失速点以上的攻角时,无黏性计算无法预测失速已经发生,因此大大高估了升力。
在势流理论中,流体假定为无旋流,也就是微小的流体质点没有净旋转速率。在数学上,这可以用速度向量场的旋度处为零来表示。无旋流有个很方便的性质,即速度可以表示为称为“位势”(potential)的纯量函数的梯度。以这种方法表示的流动称为势流。[99][100][101][102]
在势流理论中,假设流动是不可压缩的。不可压缩势流理论的优点是要求解的势流方程(拉普拉斯方程)是线性的,这允许方程式的解可透过叠加其他已知的解来构造。不可压缩势流方程也可以透过保角映射来解决,这是一种基于复变函数理论的方法。在20世纪初,在计算机出现之前,保角映射被用来求解一类理想化机翼形状的不可压缩势流方程,为升力机翼上的压力分布提供一些最早的实用的理论预测。
位势方程的解只直接决定了速度场。压力场则是由伯努利方程从速度场推导出。

将势流理论应用于升力流需要特殊的处理方法和一个额外的假设。如此便产生了问题,因为在无黏性流动中,机翼上要产生升力需要在机翼周围的流动有环量(见下面的“环量与库塔-儒可夫斯基定理”),但是单一的势函数在翼型周围的区域是连续的,不能代表该流动有著非零环量。解决这个问题的方法是引入一个分枝切割(Branch cut),即引入从机翼表面上某点到无限远处的一条曲线或直线,并允许势函数值跳过切割处。这使得流动的环量等于位势跳变(potential jump),因此得以表示为非零环量。然而,位势跳变是自由参数,不由位势方程或其他边界条件决定,因此解是不确定的。对于任何数值的环量和升力,都会存在一个势流解。解决这种不确定性的方法之一是强加库塔条件,[103][104]即在所有可能的解中,物理上合理的解是气流平稳地离开后缘的解。流线示意图说明了一种升力为零的流型(flow pattern),即气流会绕过后缘,在到达后缘之前就先离开上表面;另一种升力为正的流型则依库塔条件,气流在后缘平稳地离开。
这是进一步假设翼型很薄和攻角很小的势流理论。[105]线性化理论预测了翼型压力分布的一般特征,以及翼型形状和攻角对压力分布的影响,但对设计工作来说不够准确。一个二维翼型的计算可在几分之一秒内在个人电脑上的电子试算表中完成。

当翼型产生升力时,整体速度场会有几个分量为翼型周围的空气带来净环量:气流在翼型前面向上流动,流经上方时加速,下方的流动减速,到翼型后面时则向下流动。
这种环量可以理解为翼型周围无黏性流体的“旋转程度”(或涡量)之总量。
库塔-儒可夫斯基定理将二维翼型每单位翼展宽度的升力与流动的环流份量联系起来。[81][106][107]这是解释升力的一个关键因素,升力是随著翼型从静止开始运动时翼型周围气流的发展而产生,翼型从静到动会形成一个起动涡留在后方,导致翼型周围环量的形成。[108][109][110]接著从库塔-儒可夫斯基定理可推导出升力。这种解释很大程度上是数学上的,其一般进展是基于逻辑推理,而不是物理因果关系。[111]
库塔-儒可夫斯基模型无法预测二维机翼将产生多少环量或升力。 使用库塔-儒可夫斯基定理计算每单位翼展的升力需要已知的环量值。 特别是,如果满足库塔条件,即后驻点移动到翼型后缘并在飞行期间附著在上面,升力就可以利用保角映射法从理论上计算出来。
传统翼型产生的升力由其设计和飞行条件决定,如前进速度、攻角和空气密度。还可以人为加入环量来提高升力,例如透过从边界面的内部吹气(boundary-layer blowing)或使用吹气式襟翼(blown flap)。在佛来纳转子推进器(Flettner rotor propeller)中,整个翼型是圆形的,并绕著翼展轴旋转来建立环量。
三维流动


围绕三维机翼的流动还涉及其他重要问题,尤其是与翼尖有关的问题。对于低展弦比的机翼,如典型的三角翼,二维理论的模型可能较差,三维流动效应占了主导地位[112]。即使对于高展弦比的机翼,有限翼展的三维效应也会影响整个翼展,而不会只影响靠近翼尖的地方。
翼尖的垂直压力梯度会导致空气侧向流动,然后从机翼下方出去,回到上表面。 这降低了翼尖处的压力梯度,因此也降低了升力。升力在翼展方向上(从翼根到翼尖)趋于减小,翼型截面周围的压力分布也在翼展方向上有相应变化。在与飞行方向垂直的方向上,飞机的压力分布有著如右图所示的倾向。[113]这种沿翼展变化的压力分布是透过与速度场的相互作用来维持的。机翼下方的气流向外侧加速,机尖外侧的气流向上加速,机翼上方的气流向内侧加速,这就形成了如右图所示的流型。[114]
与具有相同翼型形状和截面升力的二维流相比,这种流动有著更多的向下偏转,并且与二维流相比需要更高的截面攻角来实现相同的升力。[115]机翼实际上是在自己制造的下沉气流(downdraft)中飞行,就像自由气流向下倾斜一样,其结果是空气动力向量的总和与二维情况相比略微向后倾斜。这个力向量多出来的后向分量称为升力诱导阻力。
机翼上方和下方的速度在翼展方向上的分量差异(上方内侧方向和下方外侧方向之间)在后缘和下游的尾流中持续存在。在气流离开后缘后,这种速度差发生在相对较薄的剪切层上,称为涡流面(vortex sheet)。
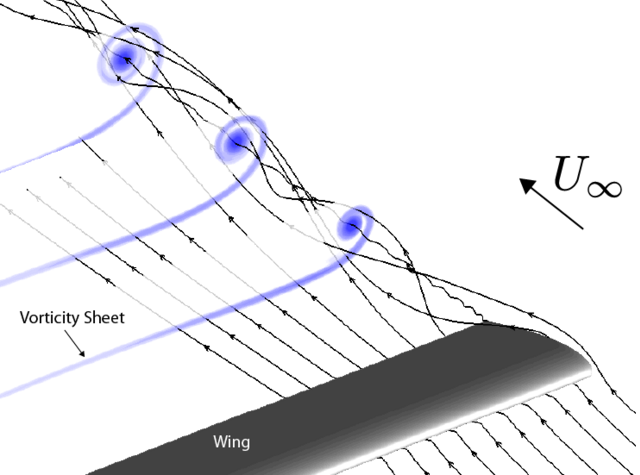

离开机翼的翼尖流产生翼尖涡流。当主涡流面从后缘向下游移动时,会在其外缘处卷起,与翼尖涡流合并。翼尖涡流与补充其的涡流面的组合称为涡迹流(vortex wake)。
除了尾部涡迹流中的涡量外,机翼边界层中也有涡量,称为“束缚涡漩”或“附著涡漩”(bound vorticity),它将机翼两侧的尾部涡流面连接成一个马蹄形的涡流系统。1907年,英国航空先驱兰彻斯特认识到马蹄形涡流系统的存在。[116]
给定束缚涡漩和尾流涡量的分布,必欧-沙伐定律(向量微积分关系式)可用于计算由机翼升力在场中任何位置所引起的速度扰动。 三维机翼的升力分布和升力诱导阻力的近似理论即基于这种应用于机翼马蹄涡系统的分析。[117][118]在这些理论中,束缚涡漩通常被理想化,并假设位于机翼内的曲面处。
因为在这些理论中,速度是从涡量推导出来的,所以一些作者描述了这种情况,以暗示涡量是速度扰动的原因,例如使用“涡流引致的速度”(the velocity induced by the vortex)等术语。[119]但以这种方式在涡量和速度之间赋予机械式的因果关系,与物理学并不一致。[120][121][122]机翼周围流动的速度扰动实际上是由压力场产生的。[123]
相关
参考资料
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads




