非凸大斜方截半二十面体

在几何学中，非凸大斜方截半二十面体是一种非凸均匀多面体^[5]，由62个面、120条边和60个顶点组成^[6]，其索引为U₆₇，对偶多面体为大鸢形六十面体（英语：Great deltoidal hexecontahedron）^[2]，具有二十面体群对称性（英语：Icosahedral symmetry），^[6][7]可以视为大十二面截半二十面体的刻面（英语：Faceting）多面体。^[8]在施莱夫利符号中，非凸大斜方截半二十面体可以表示为t_0,2{5⁄3,3}或${\displaystyle r^{\prime }{\begin{Bmatrix}3\\{\tfrac {5}{2}}\end{Bmatrix}}}$^[1]:162[2]，在考克斯特—迪肯符号（英语：Coxeter-Dynkin diagram）中可以表示为，在威佐夫记号中可以表示为3 5⁄3 | 2^[3][4][2]。

此条目的主题是非凸的星形均匀多面体。关于同名的阿基米德立体，请见“大斜方截半二十面体”。

非凸大斜方截半二十面体

类别	均匀星形多面体
对偶多面体	大鸢形六十面体（英语：Great deltoidal hexecontahedron）
识别
名称	非凸大斜方截半二十面体 great rhombicosidodecahedron uniform great rhombicosidodecahedron nonconvex great rhombicosidodecahedron quasirhombicosidodecahedron
参考索引	U67, C84, W105
鲍尔斯缩写 （verse-and-dimensions的wikia：Bowers acronym）	qrid
数学表示法
施莱夫利符号	t0,2{5⁄3,3} ${\displaystyle r^{\prime }{\begin{Bmatrix}3\\{\tfrac {5}{2}}\end{Bmatrix}}}$[1]:162[2]
威佐夫符号 （英语：Wythoff symbol）	3 5⁄3 | 2[3][4][2]
性质
面	62
边	120
顶点	60
欧拉特征数	F=62, E=120, V=60 （χ=2）
组成与布局
面的种类	20个正三角形 30个正方形 12个正五角星
顶点图	3.4.5/3.4
对称性
对称群	Ih, [5,3], *532
图像
3.4.5/3.4 （顶点图） 大鸢形六十面体（英语：Great deltoidal hexecontahedron） （对偶多面体）

非凸大斜方截半二十面体与小斜方截半二十面体拓朴同构^[8]，其骨架图在拓朴学上是等价的^[9]。

这个多面体与凸大斜方截半二十面体同名。

性质

非凸大斜方截半二十面体共有62个面、120条边和60个顶点。^[6]在其62个面中，有20个正三角形、30个正方形和12个正五角星^{[5]:134[10][11]}，在这些面中，共有12个非凸面和12个自相交面^[4]。若排除互相相交与自相交面，作为一个简单多面体则其外部面共有980个。^[12]

非凸大斜方截半二十面体的欧拉示性数为：

V-E+F = 60 - 120 + (20+12+30) = 2

因此这个多面体同胚于球体。^[10]

其60个顶点每个顶点都是2个正方形、一个五角星和一个正三角形的公共顶点，并依照五角星、正方形、三角形、正方形的顺序在顶点周围来列，并形成了一个交叉四边形，在顶点图中，这样的顶角可以用[5/3,4,3,4]或来表示^[8]

二面角

非凸大斜方截半二十面体有两种二面角，分别为正方形面与三角形面的二面角以及正方形与五角星的二面角。

正方形与三角形的二面角约为69度：^[13]

${\displaystyle \arccos \left({\frac {{\sqrt {15}}-{\sqrt {3}}}{6}}\right)\approx 1.205932498681\approx 69.094842552^{\circ }}$

正方形与五角星的二面角约为58.28度^[8]或视为反向相接的301.71747度^[13]：

${\displaystyle \arccos \left({\frac {\sqrt {10\left(5-{\sqrt {5}}\right)}}{10}}\right)\approx 1.01722196789785\approx 58.282526^{\circ }}$

尺寸

若非凸大斜方截半二十面体的边长为单位长，则其外接球半径为：^[14]:1250[2]

${\displaystyle R={\frac {\sqrt {11-4{\sqrt {5}}}}{2}}}$

分类

非凸大斜方截半二十面体的顶点图为交叉梯形且具备点可递的特性，同时，其存在自相交的面，因此非凸大斜方截半二十面体是一种自相交拟拟正多面体（Self-Intersecting Quasi-Quasi-Regular Polyhedra）。自相交拟拟正多面体一共有12种^[15]，除了小双三角十二面截半二十面体外，其馀由阿尔伯特·巴杜罗（Albert Badoureau）于1881年发现并描述。^[16]

自相交拟拟正多面体
（Self-Intersecting Quasi-Quasi-Regular Polyhedra）

小立方立方八面体	大立方截半立方体	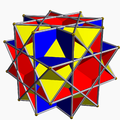非凸大斜方截半立方体	小十二面截半二十面体
大十二面截半二十面体	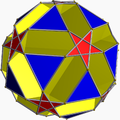小双三角十二面截半二十面体	大双三角十二面截半二十面体	二十面化截半大十二面体
小二十面化截半二十面体	大二十面化截半二十面体	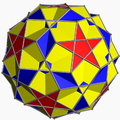斜方截半大十二面体	非凸大斜方截半二十面体

相关多面体

非凸大斜方截半二十面体与截角大十二面体以及6（英语：Compound_of_six_pentagonal_prisms）和12复合五角柱（英语：Compound_of_twelve_pentagonal_prisms）共用相同的顶点布局。同时，其亦与大十二面截半二十面体和大斜方十二面体共用相同的边布局。^[8]

非凸大斜方截半二十面体	大十二面截半二十面体	大斜方十二面体
截角大十二面体	六复合五角柱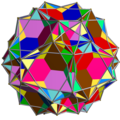（英语：Compound_of_six_pentagonal_prisms）	十二复合五角柱（英语：Compound_of_twelve_pentagonal_prisms）

参见

• 均匀星形多面体