面积

面积（英语：Area）是用作表示一个曲面或平面图形所占范围的量，可看成是长度（一维度量）及体积（三维度量）的二维类比。对三维立体图形而言，图形的边界的面积称为表面积。

计算各基本平面图形面积及基本立体图形的表面积公式早已为古希腊及古中国人所熟知。

面积在近代数学中占相当重要的角色。面积除与几何学及微积分有关外，亦与线性代数中的行列式有关。在分析学中，平面的面积通常以勒贝格测度（英语：Lebesgue measure）定义。

面积公式

其他面积公式

形状	面积	变数
三角形[1]	${\displaystyle {\tfrac {1}{2}}bh\,\!}$	${\displaystyle b}$是底，${\displaystyle h}$是高。
三角形[2]	${\displaystyle {\tfrac {1}{2}}ab\sin {\theta }\,\!}$	${\displaystyle a}$和${\displaystyle b}$是任意两条边，而${\displaystyle \theta }$是两条边的夹角。
三角形[1]	${\displaystyle {\sqrt {s(s-a)(s-b)(s-c)}}\,\!}$	${\displaystyle s}$是周长的一半，${\displaystyle a}$﹑${\displaystyle b}$和${\displaystyle c}$是三条边的长度。
等边三角形	${\displaystyle {\frac {\sqrt {3}}{4}}s^{2}\,\!}$	${\displaystyle s}$是等边三角形的边长。
等腰三角形	${\displaystyle {\frac {b}{4}}{\sqrt {(2a+b)(2a-b)}}}$	${\displaystyle a}$是腰边，${\displaystyle b}$是底边。
正方形[2]	${\displaystyle s^{2}\,\!}$	${\displaystyle s}$是正方形的边长。
长方形[2]	${\displaystyle lw\,\!}$	${\displaystyle l}$和${\displaystyle w}$分别是长方形的长和宽。
菱形、鹞形	${\displaystyle {\tfrac {1}{2}}ab}$	${\displaystyle a}$和${\displaystyle b}$分别是 菱形/鹞形 的两条对角线。
菱形	${\displaystyle a^{2}\sin {\theta }\,\!}$	${\displaystyle a}$是边长，${\displaystyle \theta }$是邻边的夹角。
平行四边形	${\displaystyle bh\,\!}$	${\displaystyle b}$是底，${\displaystyle h}$是高。
平行四边形	${\displaystyle ab\sin {\theta }\,\!}$	${\displaystyle a}$和${\displaystyle b}$是一对邻边，而${\displaystyle \theta }$是这对邻边的夹角。
梯形	${\displaystyle {\frac {(a+b)h}{2}}\,\!}$	${\displaystyle a}$和${\displaystyle b}$是平行的边，${\displaystyle h}$是平行的边之间的高。
凸四边形	${\displaystyle {\tfrac {1}{2}}xy\sin {\theta }\,\!}$	${\displaystyle x}$和${\displaystyle y}$是凸四边形两条对角线的长度，${\displaystyle \theta }$是对角线的夹角。
正五边形	${\displaystyle {\frac {5}{4}}s^{2}\tan 54^{\circ }\,\!}$	${\displaystyle s}$是正五边形的边长。
正六边形	${\displaystyle {\frac {3}{2}}s^{2}\tan 60^{\circ }={\frac {3{\sqrt {3}}}{2}}s^{2}}$	${\displaystyle s}$是正六边形的边长。
正六边形	${\displaystyle {\frac {3hs}{2}}}$	${\displaystyle s}$是正六边形的边长，${\displaystyle h}$是边与对边之间的距离。
正七边形	${\displaystyle {\frac {7}{4}}s^{2}\tan(64{\tfrac {2}{7}}^{\circ })\,\!}$	${\displaystyle s}$是正七边形的边长。
正八边形	${\displaystyle 2s^{2}\tan(67{\tfrac {1}{2}}^{\circ })=2(1+{\sqrt {2}})s^{2}\,}$	${\displaystyle s}$是正八边形的边长。
正九边形	${\displaystyle {\frac {9}{4}}s^{2}\tan 70^{\circ }\,\!}$	${\displaystyle s}$是正九边形的边长。
正十边形	${\displaystyle {\frac {5}{2}}s^{2}\tan 72^{\circ }\,\!}$	${\displaystyle s}$是正十边形的边长。
正多边形[3]	${\displaystyle {\frac {1}{4}}nl^{2}\cdot \cot {\frac {\pi }{n}}\,\!}$	${\displaystyle l}$是边长而${\displaystyle n}$是边数量。
正多边形	${\displaystyle {\frac {1}{4n}}p^{2}\cdot \cot {\frac {\pi }{n}}\,\!}$	${\displaystyle p}$是周长${\displaystyle n}$是边数量。
正多边形	${\displaystyle {\frac {1}{2}}nR^{2}\cdot \sin {\frac {2\pi }{n}}=nr^{2}\tan {\frac {\pi }{n}}\,\!}$	${\displaystyle R}$是外切圆的半径，${\displaystyle r}$内切圆的半径，而${\displaystyle n}$是边数量。
正多边形	${\displaystyle {\tfrac {1}{2}}ap\,\!}$	${\displaystyle a}$是边心距，或称作内切圆的半径，而${\displaystyle p}$是多边形的周长。
圆形	${\displaystyle \pi r^{2}\ {\text{or}}\ {\frac {\pi d^{2}}{4}}\,\!}$	${\displaystyle r}$是半径，${\displaystyle d}$是直径。
扇形	${\displaystyle \pi r^{2}\cdot {\frac {\theta }{360^{\circ }}}\,\!}$	${\displaystyle r}$和${\displaystyle \theta }$分别是半径和角度。
椭圆形[2]	${\displaystyle \pi ab\,\!}$	${\displaystyle a}$和${\displaystyle b}$分别是半长轴和半短轴。
圆柱体表面面积	${\displaystyle 2\pi r(r+h)\,\!}$	${\displaystyle r}$和${\displaystyle h}$分别是半径和高。
圆柱体侧表面面积	${\displaystyle 2\pi rh\,\!}$	${\displaystyle r}$和${\displaystyle h}$分别是半径和直径。
球体表面面积	${\displaystyle 4\pi r^{2}\ {\text{or}}\ \pi d^{2}\,\!}$	${\displaystyle r}$和${\displaystyle d}$分别是半径和直径。
锥体表面面积[4]	${\displaystyle B+{\frac {PL}{2}}\,\!}$	${\displaystyle B}$是底面积，${\displaystyle P}$是底周长而，${\displaystyle L}$是斜高。
锥体平截头体的表面面积[4]	${\displaystyle B+{\frac {PL}{2}}\,\!}$	${\displaystyle B}$是底面积，${\displaystyle P}$是底周长，${\displaystyle L}$是斜高。
正方形转换成圆形段面积	${\displaystyle {\frac {4}{\pi }}A\,\!}$	${\displaystyle A}$是正方形面积。
圆形转换成正方形后面积	${\displaystyle {\frac {1}{4}}C\pi \,\!}$	${\displaystyle C}$是圆形面积。
勒洛三角形	${\displaystyle {1 \over 2}(\pi -{\sqrt {3}})x^{2}}$	${\displaystyle x}$是勒洛三角形内三角形的边。

长方形的面积

这个长方形的面积是 lw.

最基本的面积公式是长方形的公式。当l是长，w是宽时，其公式为：^[2]

${\displaystyle A=lw}$

当其图形是一个正方形时，${\displaystyle l=w}$，因此正方形的公式为：^[2]

${\displaystyle A=s^{2}}$

长方形的面积计算方法需要证明。

证明^[5]

证明

引理：两个长方形面积之比等于其长宽之积之比

如图，根据《几何原本》第六卷命题一 ——等高之平行四边形的面积比与其底之比等同^[6]，我们得到

${\displaystyle {\begin{aligned}B:Y&=a:c\\&=ad:cd{\text{（ 第 五 卷 命 題 十 五 ）}},\end{aligned}}}$

又

${\displaystyle {\begin{aligned}Y:G&=b:d\\&=ab:ad{\text{（ 第 五 卷 命 題 十 五 ）}},\end{aligned}}}$

所以

${\displaystyle B:G=ab:cd{\text{（ 第 五 卷 命 題 二 十 三 ）}},}$

引理证毕。

定理：长方形的面积等于其长宽之积

根据引理， A:R=lw:(1x1)

定义单位正方形的面积为一平方单位。由于R是单位正方形，因此面积是一平方单位。将一平方单位代入R，得到：A:1=lw:1

${\displaystyle A=lw}$ （第五卷命题九）

（定理证毕）

面积相同

切割图形

有些简单的公式可以切割的方式得出。

例如平行四边形，可以切割成一个梯形和一个直角三角形，如同右图。如果三角形移到平行四边形的另一边，就可以变成一个长方形。因此，平行四边形的面积公式有点像长方形的：^[2]

${\displaystyle A=bh}$

两个全等三角形

至于同样的平行四边形可以分割为两个全等三角形。因此三角形的公式为：^[2]

${\displaystyle A={\frac {1}{2}}bh}$

圆形面积

主条目：圆的面积

圆形可以分割为很多扇形

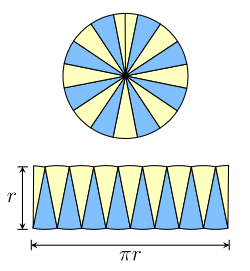
圆形面积公式是基于基本的面积公式，假设有一个半径为r的圆形，分成很多扇形，那一个扇形的面积就会很接近三角形，就像上图一样。如果分得够细小，就可以看到半径为r的圆形面积相等于一个高为r，底为πr的平行四边形。^[7]

我们也可以用积分得到更肯定的答案。

${\displaystyle A=2\int _{-r}^{r}{\sqrt {r^{2}-x^{2}}}\,dx=\pi r^{2}.}$

计算不规则之图形面积，可用填补法或切割法来计算之。

表面积

主条目：表面积

一些基本的立体表面积公式：

• 立方体：${\displaystyle 6x^{2}}$（x是立方体的边长）
• 长方体：${\displaystyle 2(lw+wh+hl)}$（l、w、h分别是长方体的长、宽和高）
• 球体：${\displaystyle 4\pi r^{2}}$（r是球体的半径）
• 球冠：${\displaystyle 2\pi rh}$（球冠是指被平面截下的部分球面；r是球体的半径；h是球冠高）
• 直立圆锥体：${\displaystyle \pi r(r+{\sqrt {r^{2}+h^{2}}})}$（r是圆锥体底部的半径，h是它的高）
• 直立圆柱体：${\displaystyle 2\pi r(h+r)}$（r是圆柱体圆形底部的半径，h是它的高）

单位列表

主要单位

面积的测量单位主要包括：

• 平方公里——1,000,000平方米
• 平方公引（ha）——10,000平方米
• 平方公丈（a）——100平方米
• 平方公尺——1平方米，国际标准单位
• 平方公寸——0.01平方米
• 平方公分——0.0001平方分米
• 平方公釐——0.000001平方厘米

市制：

• 亩——10丈 × 6丈 ——33.33米 × 20米 ——666.67平方米
• 平方市里——0.25平方公里
• 平方市尺——1/9平方米

台制：

• 甲——9,699.173平方公尺（平方米）
• 坪——3.3058平方公尺（平方米）

香港：

• 平方呎（平方英尺）——929平方厘米

换算

名称	符号	定义	与平方公尺的换算
平方昆米	Qm²	边长为1昆米的正方形的面积	1060
平方容米	Rm²	边长为1容米的正方形的面积	1054
平方佑公尺、平方尧米	Ym²	边长为1佑公尺（尧米）的正方形的面积	1048
平方皆公尺、平方泽米	Zm²	边长为1皆公尺（泽米）的正方形的面积	1042
平方艾公尺	Em²	边长为1艾公尺的正方形的面积	1036
平方拍公尺	Pm²	边长为1拍公尺的正方形的面积	1030
平方兆公尺、平方太米	Tm²	边长为1兆公尺（太米）的正方形的面积	1024
平方吉公尺	Gm²	边长为1吉公尺的正方形的面积	1018
平方百万公尺、平方兆米	Mm²	边长为1百万公尺（兆米）的正方形的面积	1012
平方公里、平方千米	km²	边长为1公里（千米）的正方形的面积	106
平方公引、平方百米、公顷	hm²	边长为1公引（百米）的正方形的面积	104
平方公丈、平方十米	dam²	边长为1公丈（十米）的正方形的面积	102
平方公尺、平方米	m²	边长为1公尺（米）的正方形的面积	1
平方公寸、平方分米	dm²	边长为1公寸（分米）的正方形的面积	10-2
平方公分、平方厘米	cm²	边长为1公分（厘米）的正方形的面积	10-4
平方公厘、平方毫米	mm²	边长为1公厘（毫米）的正方形的面积	10-6
平方微米	cm²	边长为1微米的正方形的面积	10-12
平方奈米、平方纳米	nm²	边长为1奈米（纳米）的正方形的面积	10-18
平方皮米	pm²	边长为1皮米的正方形的面积	10-24
平方飞米	fm²	边长为1飞米的正方形的面积	10-30
平方阿米	am²	边长为1阿米的正方形的面积	10-36
平方介米、平方仄米	zm²	边长为1介米（仄米）的正方形的面积	10-42
平方攸米、平方幺米	ym²	边长为1攸米（幺米）的正方形的面积	10-48
平方柔米	rm²	边长为1柔米的正方形的面积	10-54
平方亏米	qm²	边长为1亏米的正方形的面积	10-60

严格定义

主条目：若尔当测度

其中一个定义面积的方法是利用公理定义。面积可以定义为一个由所有（可测）平面图形组成的集合M映射至实数的函数a，并满足以下条件：

• 对于所有${\displaystyle S\in M}$，有${\displaystyle a(S)\geq 0}$。
• 若${\displaystyle S,T\in M}$，则${\displaystyle S\cup T\in M}$及${\displaystyle S\cap T\in M}$，且${\displaystyle a(S\cup T)=a(S)+a(T)-a(S\cap T)}$。
• 若${\displaystyle S,T\in M}$且${\displaystyle S\subseteq T}$，则${\displaystyle T-S\in M}$，且${\displaystyle a(T-S)=a(T)-a(S)}$。
• 若${\displaystyle S\in M}$且${\displaystyle S}$全等于${\displaystyle T}$，则${\displaystyle T\in M}$，且${\displaystyle a(S)=a(T)}$。
• 任一矩形${\displaystyle R}$均属于${\displaystyle M}$。若矩形的长为${\displaystyle \ell }$而宽为${\displaystyle w}$，则${\displaystyle a(R)=\ell w}$。
• 设${\displaystyle Q}$为一平面图形。若存在唯一的实数${\displaystyle c}$，使得所有满足${\displaystyle S\subseteq Q\subseteq T}$的有限个矩形的联集（finite union of rectangles）${\displaystyle S}$及${\displaystyle T}$均有${\displaystyle a(S)\leq c\leq a(T)}$，则${\displaystyle Q\in M}$，且${\displaystyle a(Q)=c}$。

可以证明，满足上述条件的函数存在。 ^[8]