时频谱

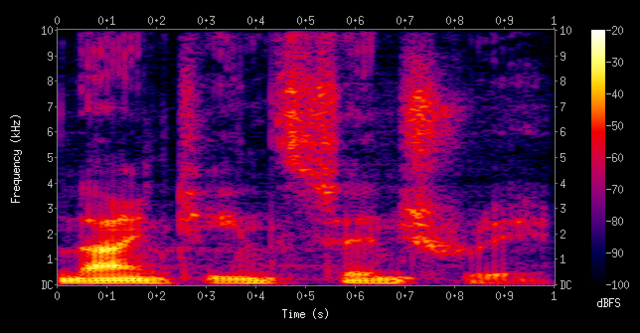
时频谱（英语：Spectrogram）又称声谱图（voicegram），是一种描述波动的各频率成分如何随时间变化的热图。利用傅里叶变换得到的传统的2维频谱可展示复杂的波动是如何按比例分解为简单波的叠加（分解为频谱），但是无法同时体现它们随时间的变化。能对波动的时间变量与频率分布同时进行分析的常用数学方法是短时距傅里叶变换，但是直接绘成3维图像的话又不便于在纸面上观察和分析。时频谱在借助时频分析方法的基础上，以热图的形式将第3维的数值用颜色的深浅加以呈现。

英文单词“nineteenth century”的发音时频谱。纵向为微小时间间隔内声波的频率分布，横向为各频率随时间的变化。最右侧的图例条表示颜色越深的区域强度越大。该图中的声音在低频率区域分布更多更密集，因为这是男声。

定义与格式

时频谱通常以热图形式呈现,即以颜色或亮度的变化来表示强度的图像。^[1]

常见格式

标准的时频谱是一个具有两个几何维度的图形:一个轴表示时间,另一个轴表示频率;第三个维度(特定频率在特定时间的振幅)由图像中每个点的强度或颜色表示。^[1]

格式有许多变化:

• 有时垂直轴和水平轴会互换,使时间由上而下排列
• 有时作为瀑布图,其中振幅由3D表面的高度而非颜色或强度表示
• 频率轴和振幅轴可以是线性或对数刻度,取决于图形的用途^[1]

对于音频,通常使用对数振幅轴(可能以分贝或dB表示)。频率可以是线性以强调谐波关系,或对数以强调音乐、音调关系。^[1]

时频分析

主条目：频谱分析和时频分析

时频分析是频谱分析的推广，比频谱分析更加直观。在分析一段随时间而变化的信号时，若单纯以离散（或离散-时间）傅立叶转换（Discrete (Time) Fourier Transform），我们能得到信号的所有频率资讯，但是却缺乏时间的资讯。以语音信号为例，若以离散傅立叶转换分析（DFT/FFT），可以得知该段声音中有哪些频率出现，却无法得知该频率出现的时间点。但若以时频分析（利用短时距傅立叶变换，STFT）来分析语音信号，我们会在每个取样时间点上乘上一个窗函数，再做离散傅立叶转换，因此在这段短时间中，我们就具有该信号的频率成分，即可得知在该段时间中，语音信号的频率为何，最后将整段信号做时频分析，就可以得到该信号的时频分布图

${\displaystyle {X}\left({t,f}\right)=\int _{-\infty }^{\infty }{w\left({t-\tau }\right)}{x}\left({\tau }\right)\,{e^{-j2\pi \,f\tau }}d\tau }$

时频谱即是描绘信号的时间和频率分布的热图，显示时频分析的结果

${\displaystyle SP(t,f)=\left|X(t,f)\right|^{2}=X(t,f)X^{*}(t,f)}$

窗函数

在计算时频谱时,窗函数的选择对结果有重要影响。窗函数用于减少频谱泄漏,但也会影响时间和频率分辨率之间的权衡。^[2]

常用窗函数类型

矩形窗(Rectangular window):

• 最简单的窗函数,在所需区段内为1,区段外为0
• 会在区段边界产生不连续,导致频域出现振铃效应
• 主瓣最窄但旁瓣电平高^[2]

汉宁窗(Hann window):

• 也称为Hanning窗,以气象学家Julius von Hann命名
• 为升馀弦窗,在边界平滑降至零
• 减少了振铃伪影,但代价是一定程度的频率模糊
• 旁瓣以约18 dB/倍频程的速率衰减^[2][3]

汉明窗(Hamming window):

• 由Richard W. Hamming提出
• 与汉宁窗类似但在端点不完全降至零(约0.08)
• 最高旁瓣约-43 dB,比汉宁窗低10 dB
• 由于端点不连续,旁瓣衰减较慢(6 dB/倍频程)^[2][3]

布莱克曼窗(Blackman window):

• 使用更多余弦项的广义窗函数
• 提供更好的旁瓣抑制(约-74 dB)
• 主瓣比汉宁窗和汉明窗宽约50%^[2]

时频分辨率权衡

窗的大小和形状可以改变。较小(较短)的窗将在时间上产生更准确的结果,但会牺牲频率表示的精确度。较大(较长)的窗将提供更精确的频率表示,但会牺牲时间表示的精确度。^[1]

这是海森堡不确定性原理的一个实例:两个共轭变量的精度乘积大于或等于一个常数(通常记为B×T≥1)。^[1][4]

进阶时频分析方法

除了基于短时距傅立叶变换的时频谱外,还有其他时频分析方法可以提供不同的时频表示。

小波变换

主条目：小波变换

连续小波变换(Continuous Wavelet Transform, CWT)是一种时频变换,特别适合分析非平稳信号。^[5]

CWT通过将信号与一组小波进行卷积来实现,这些小波由母小波(mother wavelet)经过平移和膨胀生成。数学上,CWT定义为:^[6]

${\displaystyle W(a,b)={\frac {1}{\sqrt {|a|}}}\int _{-\infty }^{\infty }x(t)\psi ^{*}\left({\frac {t-b}{a}}\right)dt}$

其中:

• ${\displaystyle W(a,b)}$ 是小波系数
• ${\displaystyle a}$ 是尺度参数(与频率成反比)
• ${\displaystyle b}$ 是时间平移参数
• ${\displaystyle \psi (t)}$ 是母小波
• ${\displaystyle \psi ^{*}}$ 表示复共轭

尺度图(Scalogram)是CWT的绝对值平方作为时间和频率函数的图形表示,类似于STFT的时频谱。^[5]

CWT相对于STFT的优势:

• 可变时频分辨率:对低频使用较长的小波以改善频率定位,对高频使用较短的小波以改善时间定位^[5]
• 克服了STFT的固定窗口大小限制
• 更适合分析包含多尺度特征的信号^[7]

常用的母小波包括:

• Morlet小波:常用于时频分析
• Haar小波:最简单的小波
• Daubechies小波系列
• 墨西哥帽小波^[5]

维格纳分布

维格纳-维尔分布(Wigner-Ville distribution, WVD)是另一种时频表示方法,定义为:^[8]

${\displaystyle W(t,\omega )=\int _{-\infty }^{\infty }x\left(t+{\frac {\tau }{2}}\right)x^{*}\left(t-{\frac {\tau }{2}}\right)e^{-j\omega \tau }d\tau }$

WVD的特点:

• 实值函数
• 提供高时频分辨率
• 存在交叉项干扰,对多分量信号会产生虚假的时频成分^[6]

为减少交叉项,发展了多种平滑WVD的变体,如伪维格纳分布(Pseudo Wigner-Ville Distribution)和Choi-Williams分布。^[6]

应用领域

语音与音频处理

时频谱广泛应用于语音识别、音乐分析和声学研究中。在早期,模拟时频谱被应用于研究鸟类叫声等动物声音。^[1]当代数字时频谱的使用对于研究动物叫声中的频率调制(FM)特别有用,FM啁啾、宽带点击音和社交谐波的区别特征最容易通过时频谱可视化。^[1]

时频谱对于协助克服言语缺陷和对严重耳聋人群进行言语训练也很有用。^[9]

梅尔时频谱与深度学习

在基于深度学习的语音合成中,首先由序列到序列模型预测时频谱(或梅尔尺度的时频谱),然后将时频谱馈送到神经声码器以生成合成的原始波形。^[1]

梅尔时频谱(Mel spectrogram)是一种特殊的时频谱,使用梅尔刻度代替线性频率刻度,并使用分贝刻度代替线性振幅来表示颜色。^[10]

梅尔尺度基于人类感知语音的研究发现,使其适合表示语音期间产生的声音的声学信息。^[11]

梅尔时频谱在深度学习中的应用:

• 语音情感识别:将音频样本转换为梅尔时频谱图像,然后用于训练卷积神经网络(CNN)模型^[12]
• 自动语音识别:梅尔时频谱提供比原始音频或MFCC更丰富的特征表示^[13]
• 音频分类:深度学习模型利用梅尔时频谱作为输入来识别和分类各种声音^[14]

其他应用

时频谱在多个领域都有应用:

• 生物医学信号处理:分析心电图、脑电图等生理信号^[1]
• 地震学:分析地震波和地震活动
• 射频系统开发:使用高清晰度时频谱
• 振动分析:振动测试工程师使用时频谱分析连续波形的频率内容^[1]

限制与信号重建

从时频谱的公式可以看出,时频谱不包含关于其所表示信号的精确甚至近似相位的信息。因此,无法反转该过程并从时频谱生成原始信号的副本。^[1]

然而,在精确初始相位不重要的情况下,可能可以生成原始信号的有用近似值。例如:

• 分析与重合成声音时频谱仪(Analysis & Resynthesis Sound Spectrograph)是一个尝试执行此操作的电脑程序^[1]
• Pattern Playback是20世纪40年代末在哈斯金斯实验室设计的早期语音合成器,将语音声学模式图片(时频谱)转换回声音^[1]

实际上,时频谱中确实存在一些相位信息,但它以另一种形式出现,即时间延迟(或群延迟),这是瞬时频率的对偶。^[15]

参见

• 广义频谱图
• 重新分布法
• 短时距傅立叶变换
• 光谱仪
• 光学频谱