热门问题
时间线
聊天
视角
減法
二元運算 来自维基百科,自由的百科全书
Remove ads
減法(英語:substraction、法語:soustraction)是四則運算之一。減法運算的本質,就是「逆着加法去尋找原數」。

例如: 中,已知 是 和 的和,其中一個加數是 ,求另一個加數 。
其中, 稱為被減數, 稱為減數, 是 和 的差。
減法遵循幾個重要的規律:
減法不像加法那樣符合交換律,即改變運算順序會一同改變結果符號。它也不滿足結合律,也就是說,當需要連續減去兩個以上的數時,減法的執行順序會影響結果。由於 是加法單位元,減去 不會改變一個數的值。
此外,減法在涉及相關運算(如加法和乘法)時也遵循可預測的規則。所有這些規則皆可從整數減法開始進行證明,並推廣至實數、乃至更廣泛的數學對象。所有遵循這些規律的通用二元運算在抽象代數中都有研究。
Remove ads
定義

已知兩個加數的和與其中一個加數,求另一個加數的運算,符號為「 」,結果為差。
在集合論中,減法通過差集定義。給定兩個集合 和 ,它們的差集 包含所有屬於 但不屬於 的元素。例如:
若 ,,則 。
此外,在可計算性理論中,由於減法在自然數上並非良定義,數與數之間的運算實際上是通過「截斷減法」或稱為monus的運算來定義的。
例如,在整數環 中,減法確保對任意 ,存在唯一的 使得 。
Remove ads
符號與表示
減法通常用被減數與減數之間的減號"-"來表示(中綴表示法的一種),運算結果則用等號「=」表示。例如:
- (2 減 1 等於 1)
- (4 減 6 等於 -2)
在某些情況下,即使沒有出現減號,減法運算亦可「約定俗成」。例如在記賬的一列數中,若下方數字以紅色顯示,則通常表示需要減去該列中較小的數,差值寫在該行下方橫線之下的位置。[1]
英語單詞subtraction(減法,名詞)來源於拉丁語動詞「subtrahere」,而該動詞本身由前綴「sub」(意為「(從)下方」)和動詞「trahere」(意為「拉拽」)複合構成。[2]因此,減法的字面含義就是「從下方拉出」或「取走」。而subtrahend(減數)則由添加動名詞後綴「-nd」派生(字面意義為「被拉出的事物」)。
Remove ads
性質
任何數減去 0 都等於其本身:。
- 非交換律:
- 非結合律:
不同的減法運算
自然數集上的減法運算不滿足封閉性:只有當被減數大於或等於減數時,差值才是自然數。例如 減去 就無法得到自然數結果。對此有兩種處理方式:
Remove ads
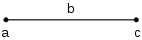
想象一條長度為 的線段,左端標記為 ,右端標記為 。從 點出發,向右移動 個單位即可到達 點。在數學上,這種右移通過加法運算建模:
而從 點出發,向左移動 個單位就能回到 點。這種左移則通過減法運算建模:

再想象一條線段,這條線段則標有數字 、 、 。現在從位置 出發,向左移動 個單位,仍停留在 ,因此 ;向左移動 個單位,則到達位置 ,因此 。
Remove ads
分數減法類似自然數和整數的減法,但要求分母相同。若兩分數分母不同,可用通分實現:
實數域可通過僅定義兩個二元運算(加法與乘法)及兩個一元運算(求加法逆元與乘法逆元)來構建。此時,從被減數中減去減數的實數運算,可定義為被減數與該減數加法逆元的加法運算。例如:
若不依賴這些一元運算,亦可將減法與除法作為基本二元運算來處理。
在線性代數中,向量空間是一個允許向量相加及縮放的代數結構。所有實數的有序對組成的集合就是一個常見的向量空間:有序對 (a, b) 被解釋為歐幾里得平面上從原點到由 (a, b) 表示的點的向量。兩個向量的差是通過將對應的坐標相減完成的:(a, b) - (c, d) = (a - c, b - d)。
大小相同的兩個矩陣可以相減。兩個 m × n 矩陣 A 和 B 的差也是一個 m × n 矩陣,用 A - B 表示,由對應元素相加得到:
設 為一個阿貝爾群。我們在 中定義一個新的內合成法則,稱為「減法」並記作"−",其定義為:
其中 表示元素 的逆元。
需要注意的是,既用"-"表示元素 的逆元 ,又表示二元運算 ,屬於符號的濫用。
一般的減法運算性質在此群論框架下依然成立。
在範疇論中,減法並沒有統一的直接對應物,但可以藉助態射、核(kernel)、余核(cokernel)、差分對象等抽象概念來表達類似於「減法」的關係。
運算方法
在美國所謂的「傳統教學」中,學生在一年級末(或二年級期間)會學習一種針對多位整數的特定豎式減法運算,該流程會在四年級或五年級時擴展至包含小數的分數表示形式。目前幾乎所有美國學校都教授一種使用借位(或稱為重組,即分解算法)的豎式減法,並配合一套被稱為"輔助記號"(crutches)的標記系統。[4][5] 雖可能不願承認,中國國內的主流算法卻正是這種「美帝算法」。
用此法計算減法時,數從右向左逐位相減。具體操作步驟如下:
- 基本減法操作:用被減數(上方數字)的每一位減去減數(下方數字)對應位置的數字。
- 借位處理:當被減數的某一位數字小於減數對應位數字時(即"上方數字太小"),則:
- 先向該位"借10"(即在當前位數字上加10)
- 同時從其左邊相鄰的高位數字中"減去1"(即高位數字減1,相當於借出1個十)
- 連續運算:完成當前位的減法後,繼續處理下一數位,根據需要重複借位操作,直至完成所有數位的減法運算。
下面以計算 為例:
-
先看被減數與減數的個位,分別是3和1。
-
3和1相減,結果是2,寫在個位上。
-
再看兩數的十位,分別是5和9。5減不了9,怎麼辦呢?
-
那就向百位「借10」!
-
15就可以減9了,結果是6,寫在十位上。
-
最後看兩數的百位,被減數餘6,減數是4。
-
6和4相減,結果是2,寫在百位上。
-
可得753和491的差是262。
美國豎式法還有一種變體,名為「先借位法」,其核心是:在進行任何減法運算之前,先完成所有的借位操作。[6]
下面以計算 為例:
-
依然先看被減數與減數的個位,分別是1和3。1減不了3,先從十位「借10」得11。
-
再看兩數的十位,被減數餘4,減數是9,同上操作得14。
-
11和3相減,結果是8,寫在個位上。
-
14和9相減,結果是5,寫在十位上。
-
最後看兩數的百位,餘下的6與4相減,結果是2,寫在百位上。
可得751和493的差是258。
部分歐洲學校採用一種稱為歐洲法(或奧地利法)的豎式減法。此法不涉及借位運算,但會根據不同國家的習慣使用各種輔助記號(幫助記憶的標記)。[7][8]
下面以計算 為例:
-
先看被減數與減數的個位,分別是3和1。
-
3=1+2,所以結果是2,寫在個位上。
-
再看兩數的十位,9加什麼等於5呢?這沒有自然數解。
-
那就從百位「借10」!被減數「變成」了15。
-
顯然,15=9+6,所以結果是6,寫在十位上。
-
最後看兩數的百位。
-
7=(4+1)+2,所以結果是2,寫在百位上。
-
可得753和491的差是262。
減法運算也可以從左到右進行。這種不常見的方法實際上是補數法的一種變體,其特點是在精確計算差值之前,先處理所有的借位(進位)問題。由於該方法既不需要記錄借位,也不需要記憶借位情況,因此不僅相對不易出現粗心錯誤,計算速度也非常快,甚至適用於心算。
下面以計算 為例:
-
先看被減數與減數的百位,7和4相減,結果是3,寫在百位上。
-
再看兩數的十位,5減不了9,怎麼辦呢?
-
當然是從百位的3「借1」!15和9相減,結果是6,寫在十位上。
-
最後看兩數的個位。
-
3和1相減,結果是2。
可得753和491的差是262。
分步差減法與其他豎式減法的相異在於:它既不需要借位,也不需要進位。取而代之的是,根據被減數與減數的大小關係,在相應數位上標註正號或負號——若被減數大於減數則記為正,反之則記為負。最終,將所有數位上的分步差值(正負結果)相加,所得總和即為最終的差值結果。[9]
下面以計算 為例:
-
先看被減數與減數的百位,700-400=300,寫在橫線下。
-
再看兩數的十位,50-90=-40,寫在橫線下「300」的下方。
-
接着看兩數的個位,3-1=2,寫在橫線下「-40」的下方。
-
最後將得到的三個新數相加:300+(-40)+2=262。
可得753和491的差是262.
不同於逐位計算差值,遞增進數法通過計算減數與被減數之間的數值增量來求得差值。[10]
示例:計算 可通過以下步驟:
將各步驟的遞增值相加即得總差值:
另一種適用於心算的方法是將減法運算拆分為多個小步驟進行計算。[11]
示例:計算 可通過以下步驟:
該方法基於"對被減數和減數同時加減相同數值不改變差值結果"的數學原理,通過調整減數至零值來簡化計算。[12]
示例:計算 可通過以下步驟:
參考資料
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads
























































































