凸分析

凸分析是研究凸函數與凸集性質的數學分支，其應用稱作凸優化，是最優化理論的子分支。

3維凸多面體。凸分析不僅包括歐氏空間凸子集的研究，還包含抽象空間上凸函數的研究。

凸集

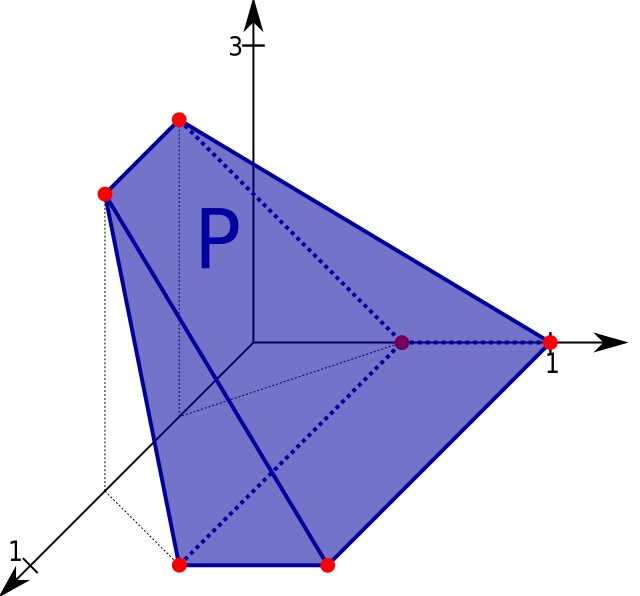
主條目：凸集

某向量空間X的子集${\displaystyle C\subseteq X}$，若滿足下列任意一條等價條件，就稱其是凸的（convex）：

1. 若${\displaystyle 0\leq r\leq 1}$是實數，${\displaystyle x,y\in C}$，則${\displaystyle rx+(1-r)y\in C.}$^[1]
2. 若${\displaystyle 0<r<1}$是實數，${\displaystyle x,y\in C,\ x\neq y,}$則${\displaystyle rx+(1-r)y\in C.}$

區間上的凸函數

主條目：凸函數

${\displaystyle f:X\to [-\infty ,\infty ]}$始終是以擴展實數線${\displaystyle [-\infty ,\infty ]=\mathbb {R} \cup \{\pm \infty \}}$為值域、以某向量空間的凸子集${\displaystyle \operatorname {domain} f=X}$為定義域的映射。 映射${\displaystyle f:X\to [-\infty ,\infty ]}$，若

${\displaystyle f(rx+(1-r)y)\leq rf(x)+(1-r)f(y)}$（凸性${\displaystyle \leq }$）

對所有實數${\displaystyle 0<r<1}$、所有${\displaystyle x,y\in X,\ x\neq y}$都成立，稱映射f是凸函數。若此不等式被替換為嚴格不等式

${\displaystyle f(rx+(1-r)y)<rf(x)+(1-r)f(y)}$（凸性${\displaystyle <}$）

對f仍成立，則稱f是嚴格凸的。^[1] 凸函數與凸集有關。特別地，當且僅當函數f的上圖（epigraph）

當且僅當函數（黑色）的上圖（即函數圖像上方區域，綠色）是凸集時，函數是凸的。

二元凸函數${\displaystyle x^{2}+xy+y^{2}}$的圖像

${\displaystyle \operatorname {epi} f:=\left\{(x,r)\in X\times \mathbb {R} ~:~f(x)\leq r\right\}}$

是凸集時，函數f是凸的。^[2]擴展實值函數的上圖在凸分析中的作用類似於實值函數圖像在實分析中的作用。特別地，擴展實值函數的上圖提供了幾何直覺，可用於形式化或證明猜想。

函數${\displaystyle f:X\to [-\infty ,\infty ]}$的定義域記作${\displaystyle \operatorname {domain} f}$，有效域則是集合^[2]

${\displaystyle \operatorname {dom} f:=\{x\in X~:~f(x)<\infty \}.}$

函數${\displaystyle f:X\to [-\infty ,\infty ]}$，當且僅當${\displaystyle \forall x\in \operatorname {domain} f,\ f(x)>-\infty ,\ \operatorname {dom} f\neq \varnothing }$，稱函數是真凸函數。^[2]這意味着在f的定義域中存在x使${\displaystyle f(x)\in \mathbb {R} }$，f也永遠不等於${\displaystyle f}$${\displaystyle -\infty }$。換句話說，若函數的定義域非空、永遠不取${\displaystyle -\infty }$、不等於${\displaystyle +\infty }$，則就是真凸函數。若${\displaystyle f:\mathbb {R} ^{n}\to [-\infty ,\infty ]}$是真凸函數，則存在向量${\displaystyle {\vec {b}}\in \mathbb {R} ^{n}}$、實數${\displaystyle r\in \mathbb {R} }$使得

${\displaystyle \forall x,\ f(x)\geq x\cdot b-r}$

其中${\displaystyle x\cdot b}$表示向量的點積。

凸共軛

主條目：凸共軛

擴展實值函數${\displaystyle f:X\to [-\infty ,\infty ]}$（不必凸）的凸共軛是來自X的（連續）對偶空間函數${\displaystyle f^{*}:X^{*}\to [-\infty ,\infty ]}$^[3]

${\displaystyle f^{*}\left(x^{*}\right)=\sup _{z\in X}\left\{\left\langle x^{*},z\right\rangle -f(z)\right\}}$

其中，括號${\displaystyle \left\langle \cdot ,\cdot \right\rangle }$表示規範對偶性${\displaystyle \left\langle x^{*},z\right\rangle :=x^{*}(z)}$。f的雙共軛是映射${\displaystyle f^{**}=\left(f^{*}\right)^{*}:X\to [-\infty ,\infty ]}$，定義為${\displaystyle \forall x\in X,\ f^{**}(x):=\sup _{z^{*}\in X^{*}}\left\{\left\langle x,z^{*}\right\rangle -f\left(z^{*}\right)\right\}}$ 將X上的Y值函數記作${\displaystyle \operatorname {Func} (X;Y)}$，則${\displaystyle f\mapsto f^{*}}$定義的映射${\displaystyle \operatorname {Func} (X;[-\infty ,\infty ])\to \operatorname {Func} \left(X^{*};[-\infty ,\infty ]\right)}$乘坐勒讓德-芬切爾變換。

次微分集與芬切爾-揚不等式

若${\displaystyle x\in X,\ f:X\to [-\infty ,\infty ]}$，則次微分集（subdifferential set）為

${\displaystyle {\begin{alignedat}{4}\partial f(x):&=\left\{x^{*}\in X^{*}~:~f(z)\geq f(x)+\left\langle x^{*},z-x\right\rangle {\text{ for all }}z\in X\right\}&&({\text{“}}z\in X{\text{''}}{\text{ can be replaced with: }}{\text{“}}z\in X{\text{ such that }}z\neq x{\text{''}})\\&=\left\{x^{*}\in X^{*}~:~\left\langle x^{*},x\right\rangle -f(x)\geq \left\langle x^{*},z\right\rangle -f(z){\text{ for all }}z\in X\right\}&&\\&=\left\{x^{*}\in X^{*}~:~\left\langle x^{*},x\right\rangle -f(x)\geq \sup _{z\in X}\left\langle x^{*},z\right\rangle -f(z)\right\}&&{\text{ The right hand side is }}f^{*}\left(x^{*}\right)\\&=\left\{x^{*}\in X^{*}~:~\left\langle x^{*},x\right\rangle -f(x)=f^{*}\left(x^{*}\right)\right\}&&{\text{ Taking }}z:=x{\text{ in the }}\sup {}{\text{ gives the inequality }}\leq .\\\end{alignedat}}}$

例如，在${\displaystyle f=\|\cdot \|}$是X上的範數這一重要特例中，可以證明^{[proof 1]}

若${\displaystyle 0\neq x\in X}$，則此定義可簡化為：

${\displaystyle \partial f(x)=\left\{x^{*}\in X^{*}~:~\left\langle x^{*},x\right\rangle =\|x\|{\text{ and }}\left\|x^{*}\right\|=1\right\}}$；${\displaystyle \partial f(0)=\left\{x^{*}\in X^{*}~:~\left\|x^{*}\right\|\leq 1\right\}.}$

${\displaystyle \forall x\in X,\ x^{*}\in X^{*},\ f(x)+f^{*}\left(x^{*}\right)\geq \left\langle x^{*},x\right\rangle ,}$這就是芬切爾-揚不等式，當且僅當${\displaystyle x^{*}\in \partial f(x)}$時是等式。正是通過這種方式，次微分集${\displaystyle \partial f(x)}$與凸共軛${\displaystyle f^{*}\left(x^{*}\right)}$直接相關。

雙共軛

函數${\displaystyle f:X\to [-\infty ,\infty ]}$的雙共軛是共軛的共軛，一般寫作${\displaystyle f^{**}:X\to [-\infty ,\infty ]}$。雙共軛有助於顯示強對偶或弱對偶何時成立（通過擾動函數）。

${\displaystyle \forall x\in X,}$不等式${\displaystyle f^{**}(x)\leq f(x)}$符合芬切爾-揚不等式。對緊合（proper）的函數，當且僅當f是凸的下半連續函數時，${\displaystyle f=f^{**}}$（芬切爾–莫羅定理）。^[3][4]

凸最小化

主條目：凸最小化

凸最小化（主）問題形如

給定凸函數${\displaystyle f:X\to [-\infty ,\infty ]}$與凸子集${\displaystyle M\subseteq X}$，求${\displaystyle \inf _{x\in M}f(x)}$

對偶問題

主條目：對偶性 (最佳化)

優化理論中，對偶原則（duality principle）指出，優化問題可以從兩個角度分別視作主問題與對偶問題。

一般來說，給定一對分離的局部凸空間${\displaystyle \left(X,X^{*}\right)}$、${\displaystyle \left(Y,Y^{*}\right)}$，以及函數${\displaystyle f:X\to [-\infty ,\infty ]}$，可以把主問題定義為求x使得

${\displaystyle \inf _{x\in X}f(x).}$

可令${\displaystyle f=f+I_{\mathrm {constraints} }}$（其中I是示性函數）將約束嵌入f。那麼讓${\displaystyle F:X\times Y\to [-\infty ,\infty ]}$是擾動函數，使得${\displaystyle F(x,0)=f(x)}$。^[5]

關於所選擾動函數的對偶問題由下式給出：

${\displaystyle \sup _{y^{*}\in Y^{*}}-F^{*}\left(0,y^{*}\right)}$

其中${\displaystyle F^{*}}$是F兩個變量的凸共軛。

對偶間隙是不等式左右兩式的差^[6][5][7]

${\displaystyle \sup _{y^{*}\in Y^{*}}-F^{*}\left(0,y^{*}\right)\leq \inf _{x\in X}F(x,0).}$

此原理同弱對偶。若兩側相等，則問題滿足強對偶。 強對偶成立的條件有很多，如

• ${\displaystyle F=F^{**}}$，其中F是連接主問題與對偶問題的擾動函數，${\displaystyle F^{**}}$是F的雙共軛；^{[來源請求]}
• 主問題是線性規劃問題；
• 凸優化問題的斯萊特條件。^[8][9]

拉格朗日對偶性

對不等式約束的凸最小化問題，

${\displaystyle \min {}_{x}f(x)}$ subject to ${\displaystyle g_{i}(x)\leq 0}$，其中${\displaystyle i=1,\ldots ,m.}$

其拉格朗日對偶問題是

${\displaystyle \sup {}_{u}\inf {}_{x}L(x,u)}$ subject to ${\displaystyle u_{i}(x)\geq 0}$，其中${\displaystyle i=1,\ldots ,m.}$

其中目標函數${\displaystyle L(x,u)}$是如下定義的拉格朗日對偶函數：

${\displaystyle L(x,u)=f(x)+\sum _{j=1}^{m}u_{j}g_{j}(x)}$

另見

• 凸性 (經濟學)
  • 非凸 (經濟學)