模糊控制

模糊控制系統是基於模糊邏輯的控制系統。模糊邏輯將模擬輸入分析為[0, 1]間連續取值的邏輯變量，不同於經典邏輯和數位邏輯只取離散值0、1（分別對應假、真）。^[1][2]該機制的輸入是透過模糊化將原本0和1的資料變成0到1之間的數值，相對於原本的非零即一的二分法較接近人類的思維。在推論的過程中資料為模糊的，但透過解模糊化的步驟，可使得輸出為精確值。

模糊邏輯在機器控制中有廣泛應用。「模糊」是說所涉邏輯能處理不能簡單表為「真」「假」，而只能表示為「部分真」。很多時候遺傳算法、人工神經網絡等方法的表現能與之媲美；不過模糊邏輯給出的解能表達為可理解的形式，這樣已有的經驗就能用在控制器設計中，使已有任務的機械化變得更容易。^[1]模糊控制常用於智能運算、建構專家系統、和類神經網路共同應用。

歷史與應用

模糊邏輯由加州大學伯克利分校控制論專家盧特菲·澤德於1965年的論文中提出。^[3]他在1973年的論文中進一步闡述了這些思想，引入了「語言變量」概念，在論文中等於被定義為模糊集的變量。之後出現了更多研究。1974年英國的E.H.Mamdani成功地將模糊控制應用於鍋爐和蒸汽機控制，1976年建於丹麥的水泥窯成為首個工業應用。^[4] 模糊系統最初在日本得到應用。

• 對模糊系統的興趣始於1985年，日立的安信誠二和宮本壯司通過仿真證明模糊控制系統在仙台市地鐵中應用的可行性。設想得到採納，1987年仙台市地鐵南北線開通時模糊系統用於控制加速、制動和停車。成為第一個成功應用模糊控制的大型工程。
• 1987年，山川健用一組簡單的專用模糊邏輯芯片，用倒單擺實驗展示了模糊控制的應用。這是一個經典控制問題，要求車通過前後移動保持頂部鉸鏈安裝的杆保持直立。山川健隨後改進了實驗，在擺的頂部放置了裝水的酒杯，甚至一隻活老鼠：系統都保持了穩定。山川健組建了自己的模糊系統研究實驗室，以幫助利用他在該領域的專利。
• 日本工程師之後為工業和消費應用開發了各種模糊系統。1988年，日本成立了國際模糊工程研究所（Laboratory for International Fuzzy Engineering，簡稱LIFE），是由48家企業構成的合作機構，旨在推進模糊研究。大眾汽車是當中唯一的外企，派遣了一名研究院參與為期三年的研究。
• 日本消費品經常採用模糊系統。松下吸塵器用運行模糊算法的單片機檢測灰塵傳感器並調整吸力；日立洗衣機用模糊控制器感應負載重量、織物混合與污垢程度，並自動設置洗滌周期，以最佳方式利用電、水和洗滌劑。
• 佳能開發了自動對焦相機，使用感光耦合元件 (CCD)測量視野中六個區域的清晰度，利用信息確定圖像是否對焦。它還能跟蹤對焦過程中鏡頭移動的變化率，並控制速度防止過沖。相機的模糊控制系統有12個輸入，6個獲取CCD的當前清晰度數據，6個測量鏡頭移動變化率；輸出是鏡頭位置。模糊控制系統共有13條規則，需要1.1KB內存。
• 三菱設計的工業空調的加熱規則和冷卻規則各有25條。溫度傳感器提供輸入，控制輸出反饋給變頻器、壓縮機閥門和風扇電機。與前一代設計相比，模糊控制器的加熱冷卻速度快5倍，功耗減少24%，溫度穩定性提高2倍，並使用更少的傳感器。
• 其他研究或實現的應用：字符與手寫識別；光學模糊系統；機器人；語音控制的機器人直升機（懸停是與倒單擺相似的「平衡行為」）；康復機器人，提供患者特定解決方案（如控制心率和血壓）；^[5]控制粉末在芯片製造中的流動；電梯系統；等等。

北美和歐洲也在進行模糊系統研究，規模不如日本那麼廣泛。

• 美國環境保護局已開始研究用於節能電機的模糊控制，NASA研究了用於太空對接的模糊控制；模擬顯示，模糊控制系統可以大大減少燃料消耗。
• 波音、通用汽車、艾倫-布拉德利、克萊斯勒集團、伊頓、惠而浦等公司已經開發模糊邏輯用於低功耗冰箱、改進的汽車變速器和節能電機。
• 1995年，美泰克（Maytag）推出了基於模糊控制器的「智能」洗碗機和「一站式感應模塊」，結合了測溫用的熱敏電阻、測量洗滌劑含量的電導率傳感器、通過散射和透射光衡量洗滌物污染程度的濁度傳感器、讀取轉速的磁致伸縮傳感器。系統能確定任何負載的最佳洗滌周期，以最少的電、洗滌劑和水量獲得最佳效果。它甚至通過跟蹤上次開門時間來調整乾燥食物的清洗，根據開門次數估計盤子數量。
• Xiera開發了第一個模糊邏輯控制器知識庫的自動調諧器——edeX。技術由莫哈克學院進行測試，能解決非線性2x2和3x3多輸入多輸出問題。^[6]

對模糊應用的研究與開發仍在進行，特別是軟件（而非固件）方面，包括模糊專家系統、模糊邏輯與神經網絡和所謂自適應「遺傳」軟件系統的整合。最終目標是構建「自學習」模糊控制系統。^[7]這些系統可用於控制複雜的非線性動態系統，如人體。ref name = "sarabadani" />^[7][8]

模糊集

參見：模糊集

模糊控制系統中的輸入變量通常是模糊集。將精確輸入值轉化為模糊值的過程稱作「模糊化」。基於模糊邏輯的方法設計兩個模糊系統，用於航向角誤差和速度控制。^[9]

控制系統也可能有各種開關，與模擬輸入一同作為輸入。其真值總等於1或0，但模糊控制可以將其視作模糊函數的特例。 給定輸入變量道成員函數和真值的映射，單片機就能根據一組「規則」決定採取什麼行動。規則的形式為

  IF brake temperature(制动温度) IS warm AND speed(速度) IS not very fast 
  THEN brake pressure(制动压力) IS slightly decreased(略微减少)

此例中，兩個輸入變量是「制動溫度」和「速度」，值由模糊集定義。輸出變量「制動壓力」也由模糊集定義，可以有「靜態」「略微增加」「略微減少」等值。

模糊控制詳解

模糊控制器在概念上很簡單：包含1個輸入段、1個處理段、1個輸出段。輸入段將來自傳感器或開關、旋鈕等的輸入映射到適當的隸屬函數和真值；處理段調用適當的規則、生成結果並組合起來；輸出段將組合結果轉換回特定的控制輸出值。

隸屬函數最常見的形狀是三角形，也有應用使用梯形、鐘形曲線，不過形狀一般不如曲線的數量和位置重要。通常3到7條曲線足以覆蓋輸入值的所需範圍，在模糊術語中這個範圍稱作「論域」。

如上所述，處理段基於一系列IF-THEN形式的邏輯規則，IF部分稱作「前件」，THEN部分稱作「後件」。典型模糊控制系統往往有數十條規則。

考慮恆溫器的一條規則：

  IF (temperature is "cold") THEN turn (heater is "high")

此規則用輸入「溫度」的真值（即「冷」的某個真值）為輸出「加熱器」生成在模糊集中的結果（「高」的某個值），與其他規則一同生成最後的明確輸出。對這一條規則而言，顯然「冷」的真值越大「高」的真值也越高，不過與其他規則綜合的最終輸出不一定是「高」。有時隸屬函數可被相當於副詞的「限制語（hedge）」修飾，常見的有「大約」「近於」「非常」「略微」「有些」等等。它們可以有精確的定義，但往往不統一。例如「非常（very）」可以是將隸屬函數平方，由於隸屬函數不大於1，這樣會縮窄隸屬函數；「極其（extremely）」可以是將隸屬函數立方，縮窄得更多；「有些（somewhat）」可以是取平方根，拓寬了隸屬函數。

實踐中，模糊規則集常常有多個前件，用模糊算子AND、OR、NOT相組合，其定義也不是統一的。比較流行的定義中，AND是取所有前件的最小值，OR則是取最大值，NOT是1減隸屬函數，得到「補」函數。

定義規則的結果有好幾種方法，最常見、最簡單的是「最大-最小」推理法，輸出隸屬函數被賦予由條件生成的真值。

規則可在硬件中並行求解，也可在軟件中順序求解。所有已觸發規則的結果通過「去模糊化」轉換為明確值，理論上有幾十種方法，各有優缺點。最常用的是「重心法（centroid）」，結果的「重心」提供明確值，偏向輸出面積最大的規則。「高度法」也很常用，即取最大貢獻者的值，偏向輸出值最大的規則。

下圖展示了一個系統的最大-最小推理和重心法去模糊化，具有輸入變量x、y、z和輸出變量n。注意mu是「真值」的標準模糊邏輯命名：

注意每條規則如何為輸出的隸屬函數提供結果作為真值。重心法去模糊化中使用OR運算（取最大值，而非相加），然後用重心計算組合結果。

模糊控制系統設計基於經驗方法，基本上是一種規範化的試錯法，一般過程如下：

• 記錄系統的操作規格、輸入和輸出。
• 記錄輸入的模糊集。
• 記錄規則集。
• 確定去模糊化方法。
• 運行測試、驗證系統，根據需要調整細節。
• 完成文檔並發布到生產環境。

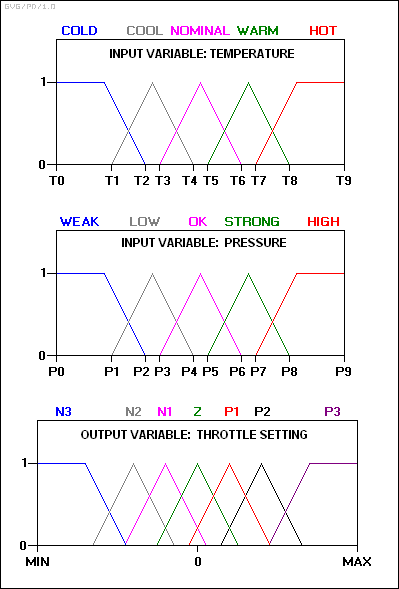
考慮為蒸汽渦輪機設計的模糊控制器作為一般例子。輸入和輸出變量映射到以下模糊集：

—當中

  N3:   大负值
  N2:   中负值
  N1:   小负值
  Z:    零
  P1:   小正值
  P2:   中正值
  P3:   大正值

規則集有以下規則：

规则1:  IF temperature IS cool AND pressure IS weak,   
         THEN throttle is P3.

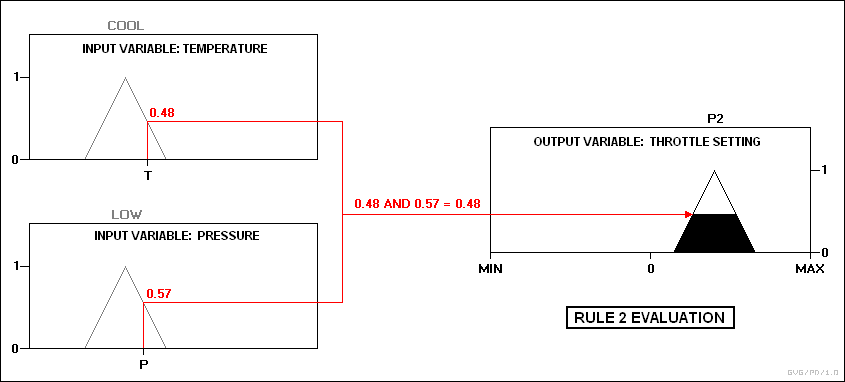
规则2:  IF temperature IS cool AND pressure IS low,    
         THEN throttle is P2.

规则3:  IF temperature IS cool AND pressure IS ok,     
         THEN throttle is Z.

规则4:  IF temperature IS cool AND pressure IS strong,
         THEN throttle is N2.

實踐中，控制器將輸入映射到隸屬函數和真值，然後將映射輸入規則。若規則規定兩輸入變量的映射間是AND關係（如上例）則以較小值為組合真值；若是OR關係則選取較大值。選擇適當的輸出狀態，並在前提的真值水平上分配隸屬度。最後對真值去模糊化。 例如，假設溫度在「涼爽」態，壓力在「低」和「正常」態，則壓力值只會觸發規則2、3：

兩個輸出通過重心法去模糊化：

   __________________________________________________________________

                                       |          Z      P2
                                    1 -+          *       *
                                       |         * *     * *
                                       |        *   *   *   *
                                       |       *     * *     *
                                       |      *       222222222
                                       |     *       22222222222
                                       |    333333332222222222222
                                       +---33333333222222222222222-->
                                                        ^ 
                                                      +150 
   __________________________________________________________________

輸出值會調節風門的開合，之後下一個控制循環生成下一個值。

構建模糊控制器

考慮用微控制器芯片實現一個簡單的反饋控制器：

為輸入變量e、誤差變化率delta、輸出output定義一個模糊集，如下：

  LP:  大正 (large positive)
  SP:  小正 (small positive)
  ZE:  零 (zero)
  SN:  小负 (small negative)
  LN:  大负 (large negative)

若誤差範圍是[-1, +1]，所用的模數轉換器分辨率為0.25，則輸入變量的模糊集（這裡也適用於輸出變量）可以總結成一張表，頂行的誤差 / 變化率 / 輸出值對應下面各行隸屬函數的真值（隸屬度）：

  _______________________________________________________________________

              -1    -0.75  -0.5   -0.25    0     0.25   0.5    0.75    1
  _______________________________________________________________________

   mu(LP)      0      0      0      0      0      0     0.3    0.7     1
   mu(SP)      0      0      0      0     0.3    0.7     1     0.7    0.3
   mu(ZE)      0      0     0.3    0.7     1     0.7    0.3     0      0
   mu(SN)     0.3    0.7     1     0.7    0.3     0      0      0      0
   mu(LN)      1     0.7    0.3     0      0      0      0      0      0
  _______________________________________________________________________            —以图形形式表示（每个“X”代表0.1的值）：

         LN           SN           ZE           SP           LP
      +------------------------------------------------------------------+
      |                                                                  |
-1.0  |  XXXXXXXXXX   XXX          :            :            :           |
-0.75 |  XXXXXXX      XXXXXXX      :            :            :           |
-0.5  |  XXX          XXXXXXXXXX   XXX          :            :           |
-0.25 |  :            XXXXXXX      XXXXXXX      :            :           |
 0.0  |  :            XXX          XXXXXXXXXX   XXX          :           |
 0.25 |  :            :            XXXXXXX      XXXXXXX      :           |
 0.5  |  :            :            XXX          XXXXXXXXXX   XXX         |
 0.75 |  :            :            :            XXXXXXX      XXXXXXX     |
 1.0  |  :            :            :            XXX          XXXXXXXXXX  |
      |                                                                  |
      +------------------------------------------------------------------+

假設本模糊系統有控制應用中的典型規則庫：

  规则1:  IF e = ZE AND delta = ZE THEN output = ZE
  规则 2:  IF e = ZE AND delta = SP THEN output = SN
  规则 3:  IF e = SN AND delta = SN THEN output = LP
  规则 4:  IF e = LP OR  delta = LP THEN output = LN

前件是誤差、誤差變化率信號的邏輯組合，後件是控制指令輸出。規則的輸出可以通過離散質心計算法解模糊化：

  SUM( I = 1 TO 4 OF ( mu(I) * output(I) ) ) / SUM( I = 1 TO 4 OF mu(I) )

假設在給定時間有

  e     = 0.25
  delta = 0.5

則會得出

  ________________________

              e     delta
  ________________________

  mu(LP)      0      0.3
  mu(SP)     0.7      1
  mu(ZE)     0.7     0.3
  mu(SN)      0       0
  mu(LN)      0       0
  ________________________

帶入規則 1：

  规则 1:  IF e = ZE AND delta = ZE THEN output = ZE

     mu(1)     = MIN( 0.7, 0.3 ) = 0.3
     output(1) = 0

-- 當中

• mu(1): 規則 1的結果隸屬函數的真值（隸屬度），質心計算中可以看做離散結果的「質量」
• output(1): 結果隸屬函數 (ZE) 在輸出變量模糊集範圍內達到最大值的位置。質心計算中，相當於單個結果的「質心」位置。這個值與mu值無關，它僅僅標示了ZE在輸出範圍上的位置

其他規則的計算結果：

  rule 2:  IF e = ZE AND delta = SP THEN output = SN

     mu(2)     = MIN( 0.7, 1 ) = 0.7   
     output(2) = -0.5

  rule 3: IF e = SN AND delta = SN THEN output = LP

     mu(3)     = MIN( 0.0, 0.0 ) = 0
     output(3) = 1

  rule 4: IF e = LP OR  delta = LP THEN output = LN

     mu(4)     = MAX( 0.0, 0.3 ) = 0.3
     output(4) = -1

質心計算法得到

  ${\displaystyle {\frac {mu(1)\cdot output(1)+mu(2)\cdot output(2)+mu(3)\cdot output(3)+mu(4)\cdot output(4)}{mu(1)+mu(2)+mu(3)+mu(4)}}}$
  ${\displaystyle ={\frac {(0.3\cdot 0)+(0.7\cdot -0.5)+(0\cdot 1)+(0.3\cdot -1)}{0.3+0.7+0+0.3}}}$
  ${\displaystyle =-0.5}$—即最终控制输出。这很简单，困难在于得到能在实践中正确工作的规则。

若不理解質心方程，只要記住質心的定義：圍繞重心的所有力矩為0。所以，記重心為${\displaystyle X_{0}}$，記每個質量位置為${\displaystyle X_{i}}$，每個質量大小為${\displaystyle M_{i}}$，有

  ${\displaystyle 0=(X_{1}-X_{0})\cdot M_{1}+(X_{2}-X_{0})\cdot M_{2}+\ldots +(X_{n}-X_{0})\cdot M_{n}}$
  ${\displaystyle 0=(X_{1}\cdot M_{1}+X_{2}\cdot M_{2}+\ldots +X_{n}\cdot M_{n})-X_{0}\cdot (M_{1}+M_{2}+\ldots +M_{n})}$
  ${\displaystyle X_{0}\cdot (M_{1}+M_{2}+\ldots +M_{n})=X_{1}\cdot M_{1}+X_{2}\cdot M_{2}+\ldots +X_{n}\cdot M_{n}}$
  ${\displaystyle X_{0}={\frac {X_{1}\cdot M_{1}+X_{2}\cdot M_{2}+\ldots +X_{n}\cdot M_{n}}{M_{1}+M_{2}+\ldots +M_{n}}}}$

我們的例子中，mu的值對應質量值，X的值對應質量的位置（不過只有當所有輸出函數的初始「質量」都相同或等效時，才能說mu「對應於質量」。如果不相同，比方說一些是窄三角形、另一些是寬梯形，就必須先得到輸出函數的質量或面積，再用mu縮放這個質量，最後乘以其位置X_i）。

此系統能在標準的微處理器上實現，現在也有專門的模糊芯片。例如加利福尼亞聖何塞的Adaptive Logic INC公司有一款模糊芯片AL220，能接收4個模擬輸入並產生4個模擬輸出。框圖如下所示：

              +---------+                              +-------+
模拟输入--4-->| 模拟多路  |                              | 多路复用器 / +--4--> 模拟输出
              |   复用器   |                            |  SH   |        
              +----+----+                              +-------+
                   |                                       ^
                   V                                       |
            +-------------+                             +--+--+
            | ADC / 锁存器 |                             | DAC |
            +------+------+                             +-----+
                   |                                       ^
                   |                                       |
                   8         +-----------------------------+
                   |         |                             |
                   |         V                             |
                   |   +-----------+      +-------------+  |
                   +-->| 模糊化器   |     |  解模糊器    +--+
                       +-----+-----+      +-------------+
                             |                   ^
                             |  +-------------+  |
                             |  |    规则     |  |
                             +->|   处理器      +--+
                                |   (50条)    |
                                +------+------+
                                       |
                                +------+------+
                                |     参数    |
                                |    存储器    |
                                |   256 x 8   |
                                +-------------+

    ADC:  模数转换器
    DAC:  数模转换器
    SH:   采样/保持器

特點

• 簡化系統設計的複雜性，特別適用於非線性、時變、模型不完全的系統上。
• 利用控制法則來描述系統變數間的關係。
• 不用數值而用語言式的模糊變數來描述系統，模糊控制器不必對被控制對象建立完整的數學模式。
• 模糊控制器是一語言控制器，使得操作人員易於使用自然語言進行人機對話。
• 模糊控制器是一種容易控制、掌握的較理想的非線性控制器，具有較佳的適應性及強健性（Robustness）、容錯（Fault Tolerance）效果較佳。

經典模糊控制器

利用模糊集合理論將專家知識或操作人員經驗形成的語言規則直接轉化為自動控制策略。通常使用模糊規則查詢表，用語言知識模型來設計和修正控制算法。

模糊控制器主要分為mamdani和TSK兩類。mamdani系統的輸入輸出均為語言值，輸出需要非模糊化得到數字量。TSK系統輸入為語言值，輸出為數字量。

模糊控制器結構

• 模糊控制器是時變參數PID控制器
• 模糊控制器的極限結構理論

設計模糊控制器一般方法

1.定義輸入及輸出變數。

通常，模糊控制的輸入變數可以是擷取自受控系統的觀測量。也可以是推導出來的資料；而模糊控制的輸出變數則為操控受控系統的操作量。設計模糊控制時，要利用一些方法去選擇適當的輸出入變數，並加以定義。

2.決定模糊化（fuzzification）的策略。

輸入到模糊控制的資料可能是代表觀測量的確定數值（crisp value），也可能是帶有模糊性質的干擾（disturbance）雜訊。設計模糊控制時必須考慮輸入信號的各種可能形式，選擇適當的模糊化方式，以便將系統的狀態轉換成語言變數。

3.定義各語言變數資料庫。

4.設計控制規則庫。

5.設計fuzzy推論機構。

6.選擇解模糊化（defuzzification）的方式。

應用

模糊控制系統適用於高度複雜、包含不確定和非線性行為、無精確數學模型的過程。成功的應用遍布世界各地，集中在1980年代以來的日本。

文獻中報告的部分應用：

• 空調^[10]
• 相機中的自動對焦系統^[11]
• 家具（冰箱、洗衣機等）^[12]
• 工業過程和系統的控制與優化^{[13][14][15][16][17]}
• 文字識別^[18]
• 引擎燃料效率^[19]
• 環境^[20]
• 專家系統^[21]
• 決策樹^[22]
• 機器人^[23][24]
• 自動駕駛汽車^[25][26][27]

另見

• 動態邏輯（英語：Dynamic logic (modal logic)）
• 貝葉斯推斷
• 函數近似（英語：Function approximation）
• 模糊概念（英語：Fuzzy concept）
• 遲滯現象
• Neuro-fuzzy（英語：Neuro-fuzzy）
• 模糊控制語言
• 2型模糊集（英語：Type-2 fuzzy sets and systems）