次方數

次方數，也稱為累乘數、冪次數（英語：Perfect power），是指一正整數n可以表示為另一正整數的平方、立方或更高次方。n為次方數的條件是存在正整數m > 0及k > 1使得m^k = n，此時n可以稱為完全k次方數，若k = 2或k = 3，n可以稱為平方數或立方數。由於針對任意正整數k，1^k = 1均成立，0^k = 0也成立，因此有時也將0, 1視為次方數。

提示：此條目的主題不是次元數。

用古氏積木說明4, 8, 9是次方數

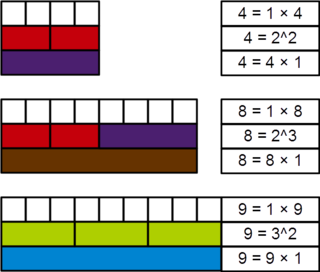
次方數的列表和倒數和

次方數數列可以用將m和k代換不同的整數值而得，以下是頭幾個次方數（允許重複數字）（OEIS數列A072103）:

${\displaystyle 2^{2}=4,\ 2^{3}=8,\ 3^{2}=9,\ 2^{4}=16,\ 4^{2}=16,\ 5^{2}=25,\ 3^{3}=27,}$ ${\displaystyle 2^{5}=32,\ 6^{2}=36,\ 7^{2}=49,\ 2^{6}=64,\ 4^{3}=64,\ 8^{2}=64,\dots }$

次方數倒數的和（其中可以有重複的次方數，像3⁴和9²都是81）為1：

${\displaystyle \sum _{m=2}^{\infty }\sum _{k=2}^{\infty }{\frac {1}{m^{k}}}=1.}$

可以用下式證明：

${\displaystyle \sum _{m=2}^{\infty }\sum _{k=2}^{\infty }{\frac {1}{m^{k}}}=\sum _{m=2}^{\infty }{\frac {1}{m^{2}}}\sum _{k=0}^{\infty }{\frac {1}{m^{k}}}=\sum _{m=2}^{\infty }{\frac {1}{m^{2}}}\left({\frac {m}{m-1}}\right)=\sum _{m=2}^{\infty }{\frac {1}{m(m-1)}}=\sum _{m=2}^{\infty }\left({\frac {1}{m-1}}-{\frac {1}{m}}\right)=1\,.}$

沒有重複的的次方數如下：

（有時會有0和1）4, 8, 9, 16, 25, 27, 32, 36, 49, 64, 81, 100, 121, 125, 128, 144, 169, 196, 216, 225, 243, 256, 289, 324, 343, 361, 400, 441, 484, 512, 529, 576, 625, 676, 729, 784, 841, 900, 961, 1000, 1024, ... （OEIS數列A001597）

沒有重複的次方數，倒數和為^[1]：

${\displaystyle \sum _{p}{\frac {1}{p}}=\sum _{k=2}^{\infty }\mu (k)(1-\zeta (k))\approx 0.874464368\dots }$

其中μ(k)是默比烏斯函數，and ζ(k)是黎曼ζ函數。

依萊昂哈德·歐拉所述，克里斯蒂安·哥德巴赫曾在信上證明（而信沒有留下），若p是0,1以外的次方數，且不考慮重複次方數，1/p − 1的和為1：

${\displaystyle \sum _{p}{\frac {1}{p-1}}={{\frac {1}{3}}+{\frac {1}{7}}+{\frac {1}{8}}+{\frac {1}{15}}+{\frac {1}{24}}+{\frac {1}{26}}+{\frac {1}{31}}}+\cdots =1.}$

有時會稱為哥德巴赫-歐拉定理。

=次方數之間的間距

2002年時，羅馬尼亞數學家Preda Mihăilescu（英語：Preda Mihăilescu）證明了唯一一組連續的次方數是2³ = 8和3² = 9，證明了卡塔蘭猜想。

Pillai猜想指出針對任意正整數k，只有有限對次方數的間距會是k，此問題目前還未解決^[2]。