Fold (高階函數)

在函數式編程中，摺疊（fold），也稱為歸約（reduce）、積累（accumulate）、聚集（aggregate）、壓縮（compress）或注入（inject），指稱一組高階函數，它們分析遞歸數據結構並通過使用給定組合運算，將遞歸的處理它的構成部件、建造一個返回值的結果重組起來。典型的，要向摺疊提供一個組合函數，一個數據結構的頂端節點（英語：Node (computer science)），和可能的在特定條件下使用的某些缺省值。摺疊接着以系統性方式使用這個函數，進行組合這個數據結構的層級中的元素。

摺疊在某種意義上是展開（英語：Anamorphism）（unfold）的對偶，它接受一個種子值並共遞歸的應用一個函數，來確定如何進一步的構造一個共遞歸的數據結構。摺疊遞歸的分解這個數據結構，在每個節點應用一個組合函數於它的終結值和遞歸結果之上，用得到這個結果替代它。摺疊是catamorphism（英語：catamorphism），而展開是anamorphism（英語：anamorphism）。

作為結構性變換

摺疊可以視為是將數據結構的結構性構件一致性的替代為函數和值。例如在很多函數式語言中，列表是用兩個原語建造的：任何列表要麼是一個空列表，通常叫做nil（[]），要麼是通過將一個元素前綴於另一個列表之前來構造的，通過應用cons函數（在Haskell中寫為冒號(:)），建立所謂的cons節點（英語：Node (computer science)），比如 Cons(X1,Cons(X2,Cons(...(Cons(Xn,nil)))))。可以將在列表上的摺疊看作是將這個列表的末端的nil替代為一個特殊的值，並用一個特殊函數替代每個cons。

使用Haskell作為例子，可以用幾個等式公式化出右摺疊foldr：

foldr :: (a -> b -> b) -> b -> [a] -> b
foldr f z []     = z
foldr f z (x:xs) = f x (foldr f z xs)

如果列表為空，結果是初始值z。如果不是空，應用f於第一個元素和摺疊餘下列表的結果。這種替代可以圖示如下：

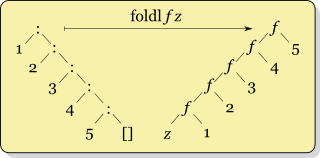
以一致性風格進行結構性變換的另一種方式，左摺疊foldl：

foldl :: (b -> a -> b) -> b -> [a] -> b
foldl f z []     = z
foldl f z (x:xs) = foldl f (f z x) xs

如果列表為空，結果是初始值。如果不是空，將應用f於舊初始值和第一個元素的結果作為新初始值，摺疊它和餘下列表。這種替代可以圖示如下：

這兩個示意圖展示在一個列表上的右摺疊和左摺疊。逐個元素的使用cons構造的列表，每個節點的左鏈接是終結值，而右鏈接是另一個節點，右摺疊之後保持這種形態。左摺疊之後，承載函數的每個節點的右鏈接是終結值，而左鏈接是另一個節點。

這兩個示意圖還突出了如下事實：id = foldr (:) []是在列表上的同一函數（按Lisp說法是「淺層複製」），因為替代cons為cons並替代nil為nil不改變結果。並提示了逆轉一個列表的一種容易的方法：reverse = foldl (flip (:)) []。注意這裡用flip函數將給cons的二個參數進行了翻轉。flip只在Haskell這樣的語言中需要，它翻轉給foldl的組合函數的實際參數的次序，不像在Scheme中，這裡對foldl和foldr二者的組合函數使用相同的實際參數次序。

另一個易得的結果是，高階函數map也可以憑藉foldr書寫，通過將要作用在元素上的那個函數複合於cons，即是：

map f = foldr ((:) . f) []

這裡的點號(.)是指示函數複合（英語：Function composition (computer science)）的算子。

通過演示在線性列表上的摺疊函數的構造方式，就會得到啟發在其他代數數據類型和結構比如各種樹之上設計類似的摺疊函數。我們可以寫一個高階函數，遞歸的將數據類型的構造子替代為所提供的函數，並將任何這個類型的常量值替代為所提供的值。這種函數一般稱為catamorphism（英語：catamorphism）。

在列表上

用加法算子摺疊列表[1,2,3,4,5]會得到結果15, 它是這個列表元素的總和。粗略近似的說，摺疊將這個列表中逗號替代成了+運算，得出了1 + 2 + 3 + 4 + 5。

在上述的例子中，+是結合律運算，所有最終的結果不管如何加括號都是相同的，儘管括號導致的特定計算次序是不同的。在非結合律二元運算的一般情況下，組合元素的次序可以影響最終的結果值。在列表之上，有二個面向的進行這個工作的方式：要麼組合第一個元素和遞歸的組合餘下列表的結果（叫做右摺疊），要麼組合遞歸的組合除了最後一個元素的所有元素的結果和最後一個元素（叫做左摺疊）。着對應於一個二元算子要麼是右結合的要麼是左結合的，採用了Haskell或Prolog的術語。使用右摺疊，合計將加括號為1 + (2 + (3 + (4 + 5)))，而使用左摺疊它將加括號為(((1 + 2) + 3) + 4) + 5。

實際上，在使用右摺疊的情況下有一個初始值同列表的最後一個元素組合，在使用左摺疊的情況下有一個初始值同和列表的第一個元素組合，是方便和自然的。在上述的例子中，值0（加法單位元）可以被選擇為初始值，對於右摺疊得到1 + (2 + (3 + (4 + (5 + 0))))，對於左摺疊得到((((0 + 1) + 2) + 3) + 4) + 5。對於乘法，選擇1（乘法單位元）作為初始值，這將得出1 * 1 * 2 * 3 * 4 * 5 = 120 = 5!。

在組合函數f的類型是不對稱的情況下，比如a -> b -> b，就是說如果結果的類型不同於列表元素的類型，使用初始值是必需的。要使一個線性的應用鏈成為可能，使用的這個初始值的類型必須同於f的結果的類型。不管是右摺疊還是左摺疊，它的類型都確定為組合函數的參數所預期的類型。如果第二個參數必須與結果相同類型，則f可以被看作是右結合的，如果是第一個參數則為左結合的。那些使用對稱類型二元運算的摺疊，它的二個參數的類型和它的結果的類型必須相同。

樹狀摺疊

在組合函數是個原群的情況下，就是說它的類型是對稱的，比如a -> a -> a，就是說結果的類型同於列表元素的類型，則可以用任意方式放置括號，因而建立嵌套子表達式的「樹」，比如((1 + 2) + (3 + 4)) + 5。如果二元運算f是結合律的，則這個值將是良好定義的，就是對於任何加括號情況，都是相同的，儘管如何計算它的運算細節會是不同的。如果f是非嚴格求值的，這可能在效能上有重大影響。 線性摺疊是面向節點的，並以一致方式對列表的每個節點進行運算；而樹狀摺疊是面向整個列表的，並以一致方式跨越節點「群」進行運算。

列表可以按樹狀風格來摺疊，分別對於有限和不明確定義的列表二者：

foldt :: (a -> a -> a) -> a -> [a] -> a
foldt f z []     = z
foldt f z [x]    = f x z
foldt f z xs     = foldt f z (pairs f xs)

foldi :: (a -> a -> a) -> a -> [a] -> a 
foldi f z []     = z
foldi f z (x:xs) = f x (foldi f z (pairs f xs))

pairs :: (a -> a -> a) -> [a] -> [a] 
pairs f (x:y:t)  = f x y : pairs f t
pairs _ t        = t

在foldi函數的情況下，為了避免在不明確定義的列表上失控求值，函數f必須「不總是」需求它的第二個參數的值，至少不是所有都要，或者不是立即就要。

非空列表的特殊摺疊

人們經常希望選擇f的單位元作為初始值z。在沒有合適的初始值的時候，例如在想要把計算它的二個參數的極大值的函數，摺疊到一個非空列表之上，來得到這個列表的極大值，可以用foldr和foldl的變體，它們分別使用這個列表的最後一個和第一個元素作為初始值。在Haskell和其他一些語言中，它們叫做foldr1和foldl1，這裡的「1」所指的是自動提供初始元素，和它們所應用到的列表至少要有一個元素的事實。

foldl1 f [x]      = x
foldl1 f (x:y:xs) = foldl1 f (f x y : xs)

foldr1 f [x]      = x
foldr1 f (x:xs)   = f x (foldr1 f xs)

foldt1 f [x]      = x
foldt1 f (x:y:xs) = foldt1 f (f x y : pairs f xs)
 
foldi1 f [x]      = x
foldi1 f (x:xs)   = f x (foldi1 f (pairs f xs))

例子

使用Haskell解釋器，摺疊進行的結構性變換可以用構造一個字符串來展示：

λ> foldr (\x y -> concat ["(",x,"+",y,")"]) "0" (map show [1..13])
"(1+(2+(3+(4+(5+(6+(7+(8+(9+(10+(11+(12+(13+0)))))))))))))"
 
λ> foldl (\x y -> concat ["(",x,"+",y,")"]) "0" (map show [1..13])
"(((((((((((((0+1)+2)+3)+4)+5)+6)+7)+8)+9)+10)+11)+12)+13)"
 
λ> foldt (\x y -> concat ["(",x,"+",y,")"]) "0" (map show [1..13])
"(((((1+2)+(3+4))+((5+6)+(7+8)))+(((9+10)+(11+12))+13))+0)"
 
λ> foldi (\x y -> concat ["(",x,"+",y,")"]) "0" (map show [1..13])
"(1+((2+3)+(((4+5)+(6+7))+((((8+9)+(10+11))+(12+13))+0))))"

無限樹狀摺疊，可以用Haskell的通過埃拉托斯特尼篩法的遞歸素數生成來演示：

primes = 2 : _Y ((3 :) . minus [5,7..] . foldi (\(x:xs) ys -> x : union xs ys) [] 
                       . map (\p-> [p*p, p*p+2*p..]))
_Y g = g (_Y g)     -- = g . g . g . g . ...

這裡的函數union以本地方式運算於有序列表之上來高效的產生它們的併集，而minus 做它們的集合差。

對於有限列表，歸併排序（和它的去除重複變體nubsort）可以使用樹狀摺疊輕易的定義為：

mergesort xs = foldt merge [] [[x] | x <- xs]
nubsort   xs = foldt union [] [[x] | x <- xs]

採用的函數merge是union的保留重複的變體。

函數head和last也可以通過摺疊定義為：

head = foldr (\x r -> x) (error "head: Empty list")
last = foldl (\a x -> x) (error "last: Empty list")

求值次序考慮

在採用惰性或非嚴格求值策略的場合下，foldr將立即返回f在列表頭部和摺疊餘下列表的遞歸案例上的這個應用。因此，如果f能夠產生其結果的一部份，而不需要引用到遞歸案例，它在f的「右」也就是第二個實際參數上，而餘下的結果永不需要，那麼遞歸就會停止，例如上節定義的head函數。這允許右摺疊可以運算在無限列表之上。與之相反，foldl將立即的調用具有新參數的自身，直到它達到了列表的末端。這種尾遞歸可以高效的編譯為循環，但是根本不能處理無限列表，它會永久遞歸於無限循環。

已經到達列表的末端之後，foldl有效的建造了一個「表達式」，它是嵌套的左深化f應用，它被提供給調用者進行求值。如果函數f首先引用它的第二個參數，並且能夠產生其結果的一部份，而不需要引用到遞歸案例，這裡是在它的「左」也就是第一個實際參數上，那麼遞歸會停止，例如上節定義的last函數。這意味着儘管foldr遞歸「於右側」，它允許惰性組合函數來從左至右檢查列表的元素；而反過來，儘管foldl遞歸「於左側」，它允許惰性組合函數從從右至左檢查列表的元素。

逆轉一個列表也是尾遞歸的，它可以使用rev = foldl (\ys x -> x : ys) []實現。在有限列表上，這意味着左摺疊和逆轉可以複合起來以尾遞歸方式進行右摺疊，通過修改f使它逆轉其參數的次序，例如foldr f z == foldl (flip f) z . rev，這樣尾遞歸的建造出的一個表達式的表示同於右摺疊所建造的。

額外的中間列表結構可以通過形似傳遞續體風格（英語：continuation-passing style）的手段去除：foldr f z xs == foldl (\k x-> k . f x) id xs z；另一個在也類似：foldl f z xs == foldr (\x k-> k . flip f x) id xs z。它們也常被寫為^[1]：

foldr :: (a -> b -> b) -> b -> [a] -> b
foldr f z xs = foldl (\k x y -> k (f x y)) id xs z

foldl :: (b -> a -> b) -> b -> [a] -> b
foldl f z xs = foldr (\x k y -> k (f y x)) id xs z

另一個技術要點是，在使用惰性求值的左摺疊的情況下，新初始化參數在進行遞歸調用之前是不被求值的。在達到了列表末端並嘗試計算結果的巨大的表達式的時候，這可能導致堆棧溢出。為此，這種語言經常提供左摺疊的更嚴格變體，它在進行遞歸調用之前強制的求值初始化參數。在Haskell中它是Data.List庫里的foldl'函數（注意這個撇號讀作「prime」）。需要意識到一個事實，強制一個值用惰性數據構造子建造，其自身不會自動的強制它的構件。結合於尾遞歸，這種摺疊接近了循環的效率，在惰性求值的最終結果是不可能或不可取的時候，確保了恆定空間運算。

在各種語言中

語言	左fold	右fold	無初始值左fold	無初始值右fold	Unfold	注釋
APL	func⍨/⌽initval,vector	func/vector,initval	func⍨/⌽vector	func/vector
C# 3.0	ienum.Aggregate(initval, func)	ienum.Reverse().Aggregate(initval, func)	ienum.Aggregate(func)	ienum.Reverse().Aggregate(func)		Aggregate是擴展方法（英語：Extension method） ienum是IEnumerable<T> 在所有的.NET語言中都類似
C++	std::accumulate(begin, end, initval, func)	std::accumulate(rbegin, rend, initval, func)				在頭文件 <numeric>中 begin, end, rbegin, rend是迭代器 func可以是一個函數指針或函數對象
C++17	(initval op ... op pack)	(pack op ... op initval)	(... op pack)	(pack op ...)		Fold表達式（只用於變元函數模板）：op是二元算子（兩個op必須相同，比如(std::cout << ... << args))， pack是未展開的參數包。
CFML（英語：ColdFusion Markup Language）	obj.reduce(func,initial)		obj.reduce(func)			這裡的func接受為實際參數的是前面運算的結果（或在第一次迭代上的initial值）；當前項；當前項的索引或鍵；和到obj的引用。
Clojure	(reduce func initval list)	(reduce func initval (reverse list'))	(reduce func list)	(reduce func" (reverse list))		參見clojure.core.reducers/fold[2]
Common Lisp	(reduce func list :initial-value initval)	(reduce func list :from-end t :initial-value initval)	(reduce func list)	(reduce func list :from-end t)
Curl	{{TreeNode.default treeNode ...} .to-Iterator}	{{TreeNode.default treeNode ...} .reverse}.to-Iterator}	{for {treeNode.to-Iterator} do}	{for {{treeNode.reverse}.to-Iterator} do}		還有DefaultListModel和HashTable實現to-Iterator
D	reduce!func(initval, list)	reduce!func(initval, list.reverse)	reduce!func(list)	reduce!func(list.reverse)		在模塊std.algorithm中
Elixir	List.foldl(list, acc, fun)	List.foldr(list, acc, fun)				樣例用法見於documentation[3]
Elm	List.foldl(Fun, Accumulator, List)	List.foldr(Fun, Accumulator, List)				參見List API[4]
Erlang	lists:foldl(Fun, Accumulator, List)	lists:foldr(Fun, Accumulator, List)
F#	Seq/List.fold func initval list	List.foldBack func list initval	Seq/List.reduce func list	List.reduceBack func list	Seq.unfold func initval
Gosu（英語：Gosu (programming language)）	Iterable.fold(f(agg, e))Iterable.reduce(init, f(agg, e)) Iterable.partition(f(e))					都是在java的Iterable接口上的擴展方法（英語：extension methods），數組也支持。
Groovy	list.inject(initval, func)	list.reverse().inject(initval, func)	list.inject(func)	list.reverse().inject(func)
Haskell	foldl func initval list	foldr func initval list	foldl1 func list	foldr1 func list	unfoldr func initval	對於foldl，摺疊函數接受參數的次序與foldr的次序相反。
Haxe	Lambda.fold(iterable, func, initval)
J	verb~/|. initval,array	verb/ array,initval	verb~/|. array	verb/ array		u/y應用二元u於y的項目之間。參見"J Dictionary: Insert"[5]
Java 8+	stream.reduce(initval, func)		stream.reduce(func)
JavaScript 1.8 ECMAScript 5	array.reduce(func, initval)	array.reduceRight(func, initval)	array.reduce(func)	array.reduceRight(func)
Julia	foldl(op, itr; [init])	foldr(op, itr; [init])	foldl(op, itr)	foldr(op, itr)
Kotlin	Iterable.fold(initval, func)	Iterable.foldRight(initval, func)	Iterable.reduce(func)	Iterable.reduceRight(func)		其他搜集也支持fold[6]和reduce[7]。還有Result.fold(onSuccess, onFailure)[8]，它歸約Result<T>（要麼成功要麼失敗）成onSuccess和onFailure的返回類型。
LFE（英語：LFE (programming language)）	(lists:foldl func accum list)	(lists:foldr func accum list)
Logtalk（英語：Logtalk）	fold_left(Closure, Initial, List, Result)	fold_right(Closure, Initial, List, Result)				meta標準庫對象提供元謂詞。縮寫foldl和foldr也可以使用。
Maple	foldl(func, initval, sequence)	foldr(func, initval, sequence)
Mathematica	Fold[func, initval, list]	Fold[func, initval, Reverse[list]]	Fold[func, list]	Fold[func, Reverse[list]]	NestWhileList[func,, initval, predicate]	不帶初始值的Fold在版本10.0和更高版本中支持。
MATLAB	fold(@func, list, defaultVal)	fold(@func, flip(list), defaultVal)	fold(@func, list)	fold(@func, flip(list))		要求Symbolic Math Toolbox，從R2016b開始支持。
Maxima	lreduce(func, list, initval)	rreduce(func, list, initval)	lreduce(func, list)	rreduce(func, list)
Mythryl	fold_left func initval list vector::fold_left func initval vector	fold_right func initval list vector::fold_right func initval vector				提供的函數接受在元組中實際參數。
OCaml	List.fold_left func initval list Array.fold_left func initval array	List.fold_right func list initval Array.fold_right func array initval			Base.Sequence.unfold ~init ~f [9]
Oz	{FoldL List Func InitVal}	{FoldR List Func InitVal}
PARI/GP（英語：PARI/GP）	fold( f, A )
Perl	reduce block initval, list		reduce block list			在List::Util模塊中
PHP	array_reduce(array, func, initval)	array_reduce(array_reverse(array), func, initval)	array_reduce(array, func)	array_reduce(array_reverse(array), func)		在未提供initval的時候，使用了NULL，所以不是真正的foldl1。在PHP 5.3之前，initval只能是整數。func是一個callback[10]。參見在線的array_reduce文檔[11]。
Python 2.x	reduce(func, list, initval)	reduce(lambda x,y: func(y,x), reversed(list), initval)	reduce(func, list)	reduce(lambda x,y: func(y,x), reversed(list))
Python 3.x	functools.reduce(func, list, initval)	functools.reduce(lambda x,y: func(y,x), reversed(list), initval)	functools.reduce(func, list)	functools.reduce(lambda x,y: func(y,x), reversed(list))		在模塊functools中[12]。
R	Reduce(func, list, initval)	Reduce(func, list, initval, right=TRUE)	Reduce(func, list)	Reduce(func, list, right=TRUE)		R通過給Reduce函數的right和init實際參數，支持右摺疊和有或沒有初始值的左或右摺疊。
Ruby	enum.inject(initval, &block) enum.reduce(initval, &block)	enum.reverse_each.inject(initval, &block) enum.reverse_each.reduce(initval, &block)	enum.inject(&block) enum.reduce(&block)	enum.reverse_each.inject(&block) enum.reverse_each.reduce(&block)		在Ruby 1.8.7+中，還可以傳遞表示一個函數而非塊的一個符號。 enum是Enumeration 請注意這些右摺疊的實現對於非交換律的&block是有誤的（還有初始值放在錯誤的一側）。
Rust	iterator.fold(initval, func)	iterator.rev().fold(initval, func)
Scala	list.foldLeft(initval)(func) (initval /: list)(func)	list.foldRight(initval)(func) (list :\ initval)(func)	list.reduceLeft(func)	list.reduceRight(func)		Scala的符號式fold語法意圖重組常用來解釋摺疊運算的左或右傾斜樹[13]，已經被重釋義為一個頂級多米諾骨牌的例證[14]。來自通用Scala語法機制的冒號，憑藉顯見的中綴算子，被調用為一個方法在左操作數上，具有右操作數作為一個實際參數傳遞，或反之如果這個算子的最後字符是冒號，這裡是對稱應用的。 Scala還有使用方法list.fold(z)(op)的樹狀摺疊特徵[15]。
Scheme R6RS	(fold-left func initval list) (vector-fold func initval vector)	(fold-right func initval list) (vector-fold-right func initval vector)	(reduce-left func defaultval list)	(reduce-right func defaultval list)		srfi/1 srfi/43
Smalltalk	aCollection inject: aValue into: aBlock		aCollection reduce: aBlock			ANSI Smalltalk不定義#reduce: 但是很多實現定義了。
Standard ML	foldl func initval list Array.foldl func initval array	foldr func initval list Array.foldr func initval array				提供的函數接受在元組中的實際參數。對於foldl，摺疊函數接受實際參數的次序同於foldr的次序。
Swift	array.reduce(initval, func) reduce(sequence, initval, func)	array.reverse().reduce(initval, func)
XPath 3.1	array:fold-left( $array as array(*), $zero as item()*, $f as function(item()*, item()*) as item()*) as item()*[16] fold-left( $seq as item()*, $zero as item()*, $f as function(item()*, item()) as item()*) as item()*[17]	array:fold-right( $array as array(*), $zero as item()*, $f asfunction(item()*, item()*) as item()*) as item()*[18] fold-right( $seq as item()*, $zero as item()*, $f as function(item(), item()*) as item()*) as item()*[19]				在XPath 3.1中由於歷史原因，array和sequence類型是不相容的 -- 因此需要分離給array和給sequence的fold函數。在簽名上的不同是由於array項目的值可以是sequence，但是XPath沒有sequence的sequence。
Xtend（英語：Xtend）	iterable.fold(initval,[func])		iterable.reduce[func]

普遍性

摺疊是多態函數。對於有如下這樣定義的任何g：

g [] = v
g (x:xs) = f x (g xs)

g都可以表達為^[20]：

g = foldr f v

還有，不動點組合子可以通過摺疊實現^[21]，證明迭代可以被歸約成摺疊：

y f = foldr (\_ -> f) undefined (repeat undefined)

參見

• 聚集函數（英語：Aggregate function）
• 迭代二元關係（英語：Iterated binary operation）
• Map (高階函數)
• Filter (高階函數)
• 前綴和（英語：Prefix sum）
• 遞歸數據類型
• 遞歸算子（英語：Reduction Operator）
• 遞歸 (計算機科學)