奧爾-索末菲方程

奧爾－索末菲方程（英語：Orr–Sommerfeld equation）是流體力學中的一個特徵值方程，用以描述黏性平行流動的二維線性擾動模態。當平行層流滿足特定條件時，相應的納維-斯托克斯方程的解會變得不穩定，此時可使用奧爾－索末菲方程判斷流體動力穩定性的條件。

奧爾－索末菲方程以威廉·邁克法登·奧爾（英語：William McFadden Orr）與阿諾德·索末菲命名。

公式

圖中所示為管道流動中的基流。

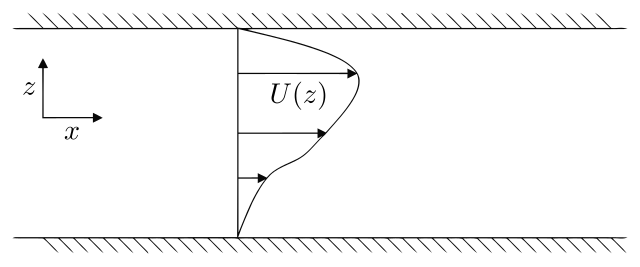
假設經擾動後的流速為

${\displaystyle \mathbf {u} =\left(U(z)+u'(x,z,t),0,w'(x,z,t)\right)}$,

其中${\displaystyle (U(z),0,0)}$為未經擾動的基流。擾動速度有類波解${\displaystyle \mathbf {u} '\propto \exp(i\alpha (x-ct))}$。使用流函數（英語：Stream function）表示流動，由線性納維-斯托克斯方程可以得到有量綱的奧爾－索末菲方程：

${\displaystyle {\frac {\mu }{i\alpha \rho }}\left({d^{2} \over dz^{2}}-\alpha ^{2}\right)^{2}\varphi =(U-c)\left({d^{2} \over dz^{2}}-\alpha ^{2}\right)\varphi -U''\varphi }$,

其中${\displaystyle \mu }$為流體的動力黏度，${\displaystyle \rho }$為流體密度，${\displaystyle \varphi }$為流函數或速度勢函數。如不考慮黏性影響，該方程可簡化為瑞利方程（英語：Rayleigh's equation (fluid dynamics)）。

無量綱形式的奧爾－索末菲方程為：

${\displaystyle {1 \over i\alpha \,Re}\left({d^{2} \over dz^{2}}-\alpha ^{2}\right)^{2}\varphi =(U-c)\left({d^{2} \over dz^{2}}-\alpha ^{2}\right)\varphi -U''\varphi }$,

其中${\displaystyle Re={\frac {\rho U_{0}h}{\mu }}}$為基流的雷諾數（${\displaystyle U_{0}}$為特徵速度，${\displaystyle h}$為管道高度）。壁面（${\displaystyle z=z_{1}}$與${\displaystyle z=z_{2}}$）的無滑移邊界條件為：

${\displaystyle \alpha \varphi ={d\varphi \over dz}=0}$（${\displaystyle \varphi }$為勢函數）

或

${\displaystyle \alpha \varphi ={d\varphi \over dx}=0}$（${\displaystyle \varphi }$為流函數）。

方程的特徵值為${\displaystyle c}$，對應的特徵向量為${\displaystyle \varphi }$。當波速${\displaystyle c}$的虛部為正時基流不穩定，微小擾動會以指數形式放大。

參考文獻

• Orr, W. M'F. The stability or instability of the steady motions of a liquid. Part I. Proceedings of the Royal Irish Academy. A. 1907, 27: 9–68.
• Orr, W. M'F. The stability or instability of the steady motions of a liquid. Part II. Proceedings of the Royal Irish Academy. A. 1907, 27: 69–138.
• Sommerfeld, A. Ein Beitrag zur hydrodynamische Erklärung der turbulenten Flüssigkeitsbewegungen. Proceedings of the 4th International Congress of Mathematicians III. Rome. 1908: 116–124.