热门问题
时间线
聊天
视角
康威多面體表示法
用来表述多面体的方法 来自维基百科,自由的百科全书
Remove ads
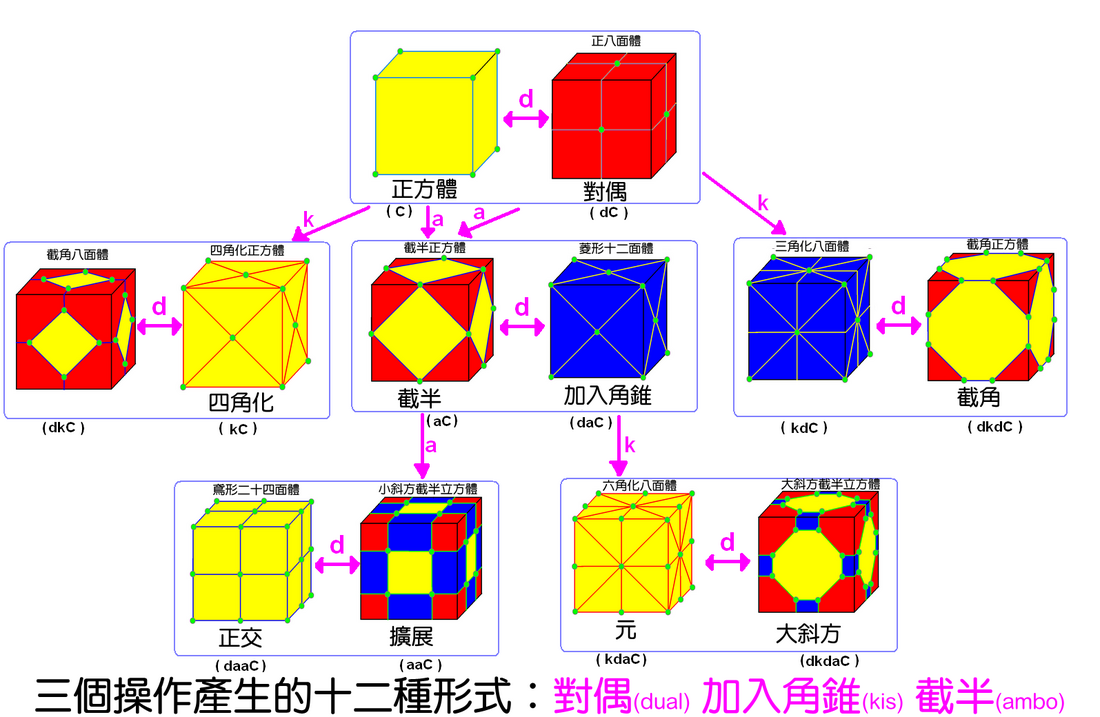
康威多面體表示法是用來描述多面體的一種方法。 一般是用種子多面體(seed)為基礎並標示對種子多面體做的操作或運算。

種子多面體一般都為正多面體或正多邊形密鋪,表示的字母則取他們名字的第一個字母,例如:
- T = 正四面體 (Tetrahedron)
- C = 正方體 (Cube)
- O = 正八面體 (Octahedron)
- D = 正十二面體 (Dodecahedron)
- I = 正二十面體 (Icosahedron)
- H = 正六邊形密鋪 (Hexagonal tiling)
- Q = 正四邊形密鋪 (Quadrille = Square tiling)
- Δ = 正三角形密鋪 (Deltille = Triangular tiling)
另外柱體和錐體也可以作為種子,並以它是底面邊數加一個字母表示:
例如種子「P5」是指五角柱、「P10」是指十角柱、「Y6」是指六角錐、「J86」是指球狀屋頂、「A86」是指86角反稜柱。
任何凸多面體皆可以當作種子,前提是它可以執行操作或運算。
何頓·康威提出這個想法, 就像開普勒的截角定義,建立相關的多面體相同的對稱性。 它的多面體表示法能從正多面體種子表示所有阿基米德立體、半正多面體和卡塔蘭立體。 在一系列的應用中,康威多面體表示法可以產生許多高階多面體。
Remove ads
多面體的運算
下面列出康威多面體表示法中,多面體的運算符號,那些運算通常類似幾何變換,並以 (v,e,f) 表示進行該運算或操作後多面體的變化。
這些運算符號的運算優先順序皆為由右至左。例如:
所有的操作都保有對稱性,除了s和g是扭曲的像並失去了鏡射對稱。
Remove ads
例子
生成標準種子
所有的五個正多面體皆可以從稜柱種子經過零至兩個運算或操作而產生:
康威的符號擴展
上述的運算和操作可以從正多面體種子或柱體錐體的種子產生所有的半正多面體、卡塔蘭立體、柏拉圖立體和阿基米德立體。 許多多面體都可由高階的組合操作還表示,但是某些特別的多面體需要更多的符號來表示。
例如,幾何藝術家George W. Hart定義他的操作稱為"propellor",和另一個反映創建鏡像圖像的旋轉形式"reflect"。
- p – "propellor" – 旋轉建立四邊形於頂點。這個操作的對偶多面體是本身: dpX=pdX。
- r – "reflect" – 對種子進行鏡射變換。一般沒已影響,除非有s或g的種子
詹森多面體擴展
為了表達詹森多面體,諾曼·詹森也定義了一些符號來表達它的多面體[1]
- 下列種子都必須要在後面加註邊數:
- 擴展的符號:
- + = 將符號後的種子加到符號前的種子之適當的面,可省略
- - = 在符號前的種子上照到跟符號後種子相同的部分並切除之
- × = 將符號前動作做符號後的次數次,符號後必為常數,可省略
- () = 將種子括號並指定動作
- 例如:
Remove ads
下面擴展符號也可以用於康威多面體表示法,但是在施萊夫利符號中,更為常用。
- t0,1 = 截角
- t0,2 = 截邊:小斜方截半
- t0,1,2 = 截邊再截角:大斜方截半
- t0,3 = 截面:向下鋸齒(Runcination) : 切割多面體,同時沿面、邊和頂點,建立新的面代替原來的面、邊和頂點中心。
- t0,1,3 = 截面再截角
- t0,2,3 = 截面再截邊
- t0,1,2,3 = 截面再截邊再截角
- t0,4 = 截胞 : 切割多胞體,同時沿胞、面、邊和頂點,建立新的胞代替原來的胞、面、邊和頂點中心。
- t1 = 截半
- t1,2 = 截半再截邊:雙截角
- t2
- h = 交替 alternate
例如:
- "hC" = 正四面體
幾何座標的衍生形式
 D |
 tD |
 aD |
 tdD |
 eD |
 teD |
 sD |
 dD |
 dteD |
 H |
 tH |
 aH |
 tdH = H |
 eH |
 teH |
 sH |
 dH |
 dtH |
 daH |
 dtdH = dH |
 deH |
 dteH |
 dsH |
Remove ads
 T |
 tT |
 aT |
 tdT |
 eT |
 bT |
 sT |
 dT |
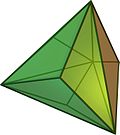 dtT |
 jT |
 kT |
 oT |
 mT |
 gT |
 {4,3,3} |
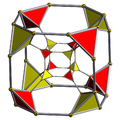 t{4,3,3} |
 a{4,3,3} |
 td{4,3,3} |
 e{4,3,3} |
 b{4,3,3} |
 s{4,3,3} |
 d{4,3,3} |
其他多面體
迭代簡單簡單操作的形式,可以產生更大的多面體,並保持基本對稱性。頂點被假設是對相同半徑的球面。
-
截角三角化四面體
"t6dtT"
-
菱形九十面體
"dakD"
-
五角化十二面體
"kD" -
五角化截半二十面體
"k5aD" -
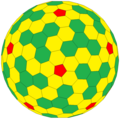
"k6k5tI"
-
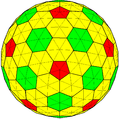
六角化五角化倒角十二面體
"kt5daD" -
"kdktI"
"dtktI" -
"kdkt5daD"
-
截角二十面體
"dkD" -
"dk6k5tI"
-
"dkt5daD"
-
"tktI"
-
"tkt5daD"
參見
外部連結和參考文獻
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads