晶系

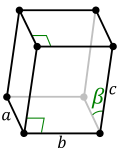
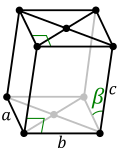
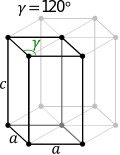
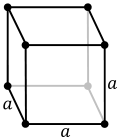
晶體通常可分為七種晶系，即立方晶系、六方晶系、四方晶系、三方晶系、正交晶系、單斜晶系、三斜晶系。其中的立方晶系具有各向同性，屬於高級晶族。

晶族	晶系	點群的對稱性	點群	空間群	布拉菲晶格	特徵	晶格系統
三斜		無	2	2	1	α≠β≠γ≠90°，a≠b≠c	三斜
單斜		1個兩次對稱軸或 1個對稱面	3	13	2	α=γ=90°，β≠90°，a≠b≠c	單斜
正交/斜方		3個兩次對稱軸或 1個兩次對稱軸+2個對稱面	3	59	4	α=β=γ=90°，a≠b≠c	正交/斜方
四方/正方		1個四次對稱軸	7	68	2	α=β=γ=90°，a=b≠c	四方/正方
六方	三方	1個三次對稱軸	5	7	1	α=β=γ≠90°，a=b=c	三方
	三方	1個三次對稱軸	5	18	1	α=β=90°，γ=120°，a=b≠c	六方
	六方	1個六次對稱軸	7	27	1	α=β=90°，γ=120°，a=b≠c	六方
立方/等軸		4個三次對稱軸	5	36	3	α=β=γ=90°，a=b=c	立方/等軸
6	7	共計	32	230	14		7

晶系	點陣常數特徵	布拉菲晶格
晶系	點陣常數特徵	簡單（P）	底心（C）	體心（I）	面心（F）
三斜晶系	a≠b≠c，α≠β≠γ≠90°
單斜晶系	a≠b≠c，α=γ=90°≠β
斜方晶系（正交晶系）	a≠b≠c，α=β=γ=90°
四方晶系	a=b≠c，α=β=γ=90°
三方晶系（棱方晶系）	a=b=c，α=β=γ≠90°
六方晶系	a=b≠c，α=β=90º，γ=120°
等軸晶系（立方晶系）	a=b=c，α=β=γ=90°

晶系	體積
三斜晶系	$abc{\sqrt {1-\cos ^{2}\alpha -\cos ^{2}\beta -\cos ^{2}\gamma +2\cos \alpha \cos \beta \cos \gamma }}$
單斜晶系	$abc\sin \alpha$
斜方晶系	$abc$
四方晶系	$a^{2}c$
三方晶系	$a^{3}{\sqrt {1-3\cos ^{2}\alpha +2\cos ^{3}\alpha }}$
六方晶系	${\frac {{\sqrt {3\,}}\,a^{2}c}{2}}$
等軸晶系	$a^{3}$

n	1	2	3	4	6
C_n	C₁	C₂	C₃	C₄	C₆
C_nv	C_1v=C_1h	C_2v	C_3v	C_4v	C_6v
C_nh	C_1h	C_2h	C_3h	C_4h	C_6h
D_n	D₁=C₂	D₂	D₃	D₄	D₆
D_nh	D_1h=C_2v	D_2h	D_3h	D_4h	D_6h
D_nd	D_1d=C_2h	D_2d	D_3d	D_4d	D_6d
S_2n	S₂	S₄	S₆	S₈	S₁₂

1	1
2		²⁄_m	222	m	mm2	mmm
3	3		32	3m	3m
4	4	⁴⁄_m	422	4mm	42m	⁴⁄_mmm
6	6	⁶⁄_m	622	6mm	62m	⁶⁄_mmm
23	m3	432	43m	m3m

晶系

晶系的特徵

布拉菲晶格

晶體學點群

熊夫利記號

赫爾曼–莫甘記號

不同記號關係

其它維度

二維

四維

參見

參考資料

外部連結

Wikiwand - on

晶族	晶系	赫爾曼–莫甘（完整記號）	赫爾曼–莫甘（簡寫記號）	舒勃尼科夫^[2]	熊夫利	軌形記號	考克斯特記號	階
三斜		1	1	$1\$	C₁	11	[ ]⁺	1
三斜		1	1	${\tilde {2}}$	C_i = S₂	x	[2⁺,2⁺]	2
單斜		2	2	$2\$	C₂	22	[2]⁺	2
		m	m	$m\$	C_s = C_1h	*	[ ]	2
		$\color {Black}{\tfrac {2}{m}}$	2/m	$2:m\$	C_2h	2*	[2,2⁺]	4
正交		222	222	$2:2\$	D₂ = V	222	[2,2]⁺	4
		mm2	mm2	$2\cdot m\$	C_2v	*22	[2]	4
		$\color {Black}{\tfrac {2}{m}}{\tfrac {2}{m}}{\tfrac {2}{m}}$	mmm	$m\cdot 2:m\$	D_2h	*222	[2,2]	8
四方		4	4	$4\$	C₄	44	[4]⁺	4
		4	4	${\tilde {4}}$	S₄	2x	[2⁺,4⁺]	4
		$\color {Black}{\tfrac {4}{m}}$	4/m	$4:m\$	C_4h	4*	[2,4⁺]	8
		422	422	$4:2\$	D₄	422	[4,2]⁺	8
		4mm	4mm	$4\cdot m\$	C_4v	*44	[4]	8
		42m	42m	${\tilde {4}}\cdot m$	D_2d	2*2	[2⁺,4]	8
		$\color {Black}{\tfrac {4}{m}}{\tfrac {2}{m}}{\tfrac {2}{m}}$	4/mmm	$m\cdot 4:m\$	D_4h	*422	[4,2]	16
六方	三方	3	3	$3\$	C₃	33	[3]⁺	3
		3	3	${\tilde {6}}$	S₆ = C_3i	3x	[2⁺,6⁺]	6
		32	32	$3:2\$	D₃	322	[3,2]⁺	6
		3m	3m	$3\cdot m\$	C_3v	*33	[3]	6
		3 $\color {Black}{\tfrac {2}{m}}$	3m	${\tilde {6}}\cdot m$	D_3d	2*3	[2⁺,6]	12
	六方	6	6	$6\$	C₆	66	[6]⁺	6
		6	6	$3:m\$	C_3h	3*	[2,3⁺]	6
		$\color {Black}{\tfrac {6}{m}}$	6/m	$6:m\$	C_6h	6*	[2,6⁺]	12
		622	622	$6:2\$	D₆	622	[6,2]⁺	12
		6mm	6mm	$6\cdot m\$	C_6v	*66	[6]	12
		6m2	6m2	$m\cdot 3:m\$	D_3h	*322	[3,2]	12
		$\color {Black}{\tfrac {6}{m}}{\tfrac {2}{m}}{\tfrac {2}{m}}$	6/mmm	$m\cdot 6:m\$	D_6h	*622	[6,2]	24
立方		23	23	$3/2\$	T	332	[3,3]⁺	12
		$\color {Black}{\tfrac {2}{m}}$ 3	m3	${\tilde {6}}/2$	T_h	3*2	[3⁺,4]	24
		432	432	$3/4\$	O	432	[4,3]⁺	24
		43m	43m	$3/{\tilde {4}}$	T_d	*332	[3,3]	24
		$\color {Black}{\tfrac {4}{m}}$ 3 $\color {Black}{\tfrac {2}{m}}$	m3m	${\tilde {6}}/4$	O_h	*432	[4,3]	48

四維晶系
No.	晶系（1985年Whittaker命名^[3]）	邊長	軸間角
1	Hexaclinic	a ≠ b ≠ c ≠ d	α ≠ β ≠ γ ≠ δ ≠ ε ≠ ζ ≠ 90°
2	Triclinic	a ≠ b ≠ c ≠ d	α ≠ β ≠ γ ≠ 90° δ = ε = ζ = 90°
3	Diclinic	a ≠ b ≠ c ≠ d	α ≠ 90° β = γ = δ = ε = 90° ζ ≠ 90°
4	Monoclinic	a ≠ b ≠ c ≠ d	α ≠ 90° β = γ = δ = ε = ζ = 90°
5	Orthogonal	a ≠ b ≠ c ≠ d	α = β = γ = δ = ε = ζ = 90°
6	Tetragonal monoclinic	a ≠ b = c ≠ d	α ≠ 90° β = γ = δ = ε = ζ = 90°
7	Hexagonal monoclinic	a ≠ b = c ≠ d	α ≠ 90° β = γ = δ = ε = 90° ζ = 120°
8	Ditetragonal diclinic	a = d ≠ b = c	α = ζ = 90° β = ε ≠ 90° γ ≠ 90° δ = 180° − γ
9	Ditrigonal (dihexagonal) diclinic	a = d ≠ b = c	α = ζ = 120° β = ε ≠ 90° γ ≠ δ ≠ 90° cos δ = cos β − cos γ
10	Tetragonal orthogonal	a ≠ b = c ≠ d	α = β = γ = δ = ε = ζ = 90°
11	Hexagonal orthogonal	a ≠ b = c ≠ d	α = β = γ = δ = ε = 90°, ζ = 120°
12	Ditetragonal monoclinic	a = d ≠ b = c	α = γ = δ = ζ = 90° β = ε ≠ 90°
13	Ditrigonal (dihexagonal) monoclinic	a = d ≠ b = c	α = ζ = 120° β = ε ≠ 90° γ = δ ≠ 90° cos γ = −1/2cos β
14	Ditetragonal orthogonal	a = d ≠ b = c	α = β = γ = δ = ε = ζ = 90°
15	Hexagonal tetragonal	a = d ≠ b = c	α = β = γ = δ = ε = 90° ζ = 120°
16	Dihexagonal orthogonal	a = d ≠ b = c	α = ζ = 120° β = γ = δ = ε = 90°
17	Cubic orthogonal	a = b = c ≠ d	α = β = γ = δ = ε = ζ = 90°
18	Octagonal	a = b = c = d	α = γ = ζ ≠ 90° β = ε = 90° δ = 180° − α
19	Decagonal	a = b = c = d	α = γ = ζ ≠ β = δ = ε cos β = −1/2 − cos α
20	Dodecagonal	a = b = c = d	α = ζ = 90° β = ε = 120° γ = δ ≠ 90°
21	Diisohexagonal orthogonal	a = b = c = d	α = ζ = 120° β = γ = δ = ε = 90°
22	Icosagonal (icosahedral)	a = b = c = d	α = β = γ = δ = ε = ζ cos α = −1/4
23	Hypercubic	a = b = c = d	α = β = γ = δ = ε = ζ = 90°

四維晶體系統
晶族序	晶族（英文）	晶系（英文）	晶系序	點群	空間群	布拉菲晶格	晶格
I	Hexaclinic		1	2	2	1	Hexaclinic P
II	Triclinic		2	3	13	2	Triclinic P, S
III	Diclinic		3	2	12	3	Diclinic P, S, D
IV	Monoclinic		4	4	207	6	Monoclinic P, S, S, I, D, F
V	Orthogonal	Non-axial orthogonal	5	2	2	1	Orthogonal KU
		Non-axial orthogonal	5	2	112	8	Orthogonal P, S, I, Z, D, F, G, U
		Axial orthogonal	6	3	887	8	Orthogonal P, S, I, Z, D, F, G, U
VI	Tetragonal monoclinic		7	7	88	2	Tetragonal monoclinic P, I
VII	Hexagonal monoclinic	Trigonal monoclinic	8	5	9	1	Hexagonal monoclinic R
		Trigonal monoclinic	8	5	15	1	Hexagonal monoclinic P
		Hexagonal monoclinic	9	7	25	1	Hexagonal monoclinic P
VIII	Ditetragonal diclinic*		10	1 (+1)	1 (+1)	1 (+1)	Ditetragonal diclinic P*
IX	Ditrigonal diclinic*		11	2 (+2)	2 (+2)	1 (+1)	Ditrigonal diclinic P*
X	Tetragonal orthogonal	Inverse tetragonal orthogonal	12	5	7	1	Tetragonal orthogonal KG
		Inverse tetragonal orthogonal	12	5	351	5	Tetragonal orthogonal P, S, I, Z, G
		Proper tetragonal orthogonal	13	10	1312	5	Tetragonal orthogonal P, S, I, Z, G
XI	Hexagonal orthogonal	Trigonal orthogonal	14	10	81	2	Hexagonal orthogonal R, RS
		Trigonal orthogonal	14	10	150	2	Hexagonal orthogonal P, S
		Hexagonal orthogonal	15	12	240	2	Hexagonal orthogonal P, S
XII	Ditetragonal monoclinic*		16	1 (+1)	6 (+6)	3 (+3)	Ditetragonal monoclinic P, S, D*
XIII	Ditrigonal monoclinic*		17	2 (+2)	5 (+5)	2 (+2)	Ditrigonal monoclinic P, RR
XIV	Ditetragonal orthogonal	Crypto-ditetragonal orthogonal	18	5	10	1	Ditetragonal orthogonal D
		Crypto-ditetragonal orthogonal	18	5	165 (+2)	2	Ditetragonal orthogonal P, Z
		Ditetragonal orthogonal	19	6	127	2	Ditetragonal orthogonal P, Z
XV	Hexagonal tetragonal		20	22	108	1	Hexagonal tetragonal P
XVI	Dihexagonal orthogonal	Crypto-ditrigonal orthogonal*	21	4 (+4)	5 (+5)	1 (+1)	Dihexagonal orthogonal G*
		Crypto-ditrigonal orthogonal*	21	4 (+4)	5 (+5)	1	Dihexagonal orthogonal P
		Dihexagonal orthogonal	23	11	20
		Ditrigonal orthogonal	22	11	41
		Ditrigonal orthogonal	22	11	16	1	Dihexagonal orthogonal RR
XVII	Cubic orthogonal	Simple cubic orthogonal	24	5	9	1	Cubic orthogonal KU
		Simple cubic orthogonal	24	5	96	5	Cubic orthogonal P, I, Z, F, U
		Complex cubic orthogonal	25	11	366	5	Cubic orthogonal P, I, Z, F, U
XVIII	Octagonal*		26	2 (+2)	3 (+3)	1 (+1)	Octagonal P*
XIX	Decagonal		27	4	5	1	Decagonal P
XX	Dodecagonal*		28	2 (+2)	2 (+2)	1 (+1)	Dodecagonal P*
XXI	Diisohexagonal orthogonal	Simple diisohexagonal orthogonal	29	9 (+2)	19 (+5)	1	Diisohexagonal orthogonal RR
		Simple diisohexagonal orthogonal	29	9 (+2)	19 (+3)	1	Diisohexagonal orthogonal P
		Complex diisohexagonal orthogonal	30	13 (+8)	15 (+9)	1	Diisohexagonal orthogonal P
XXII	Icosagonal		31	7	20	2	Icosagonal P, SN