變換幾何

在數學領域，變換幾何（英語：Transformation geometry）是一種通過聚焦於幾何變換群及在其作用下保持不變的性質來研究幾何學的教學方法。這種理念不同於以證明幾何定理為核心的歐幾里得幾何經典法。

例如，在變換幾何的框架下，等腰三角形的性質可以通過"其能夠沿某條對稱軸反射映射的圖形與自身重合"這一事實推導得出。這與古典幾何中通過三角形全等準則進行證明的方式形成鮮明對比^[1]。

將變換作為幾何學基礎的第一個系統性的探索由費利克斯·克萊因於19世紀提出，即著名的埃爾朗根綱領。約一個世紀內，該方法主要局限於數學領域。直至20世紀，教育界開始嘗試將其運用於教學領域：安德烈·柯爾莫哥洛夫在推動俄羅斯幾何教學方案改革時，將此方法（與集合論共同）納入為核心內容^[2]。這些探索在1960年代伴隨名為"新數學運動"的數學教育整體改革達到高潮。

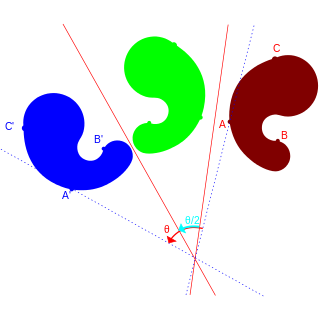
對變換幾何的探索一般始於對日常生活中反射對稱現象的研究。最初的變換是直線反射（即關於軸的反射）。兩個反射的複合會產生旋轉（當兩直線相交時）或平移（當兩直線平行時）。學生可以通過這類變換理解歐幾里得平面的等距變換。例如，考察關於垂直線和與水平線成45°夾角直線的複合反射：正向複合會產生逆時針旋轉90°，而逆向複合則會產生順時針旋轉90°。這類結果說明變換幾何包含非交換過程。

直線反射的一個應用體現在對"任意三角形中的七分之一面積三角形"的幾何證明中。

向低齡學生引入的另一類變換是放縮變換。不過圓的反演變換因其複雜性通常不適合低年級教學，因此更廣泛的反演幾何研究一般安排在大學階段。

變換幾何對具體對稱群的實驗可以為抽象群論的學習奠定基礎。而其他實踐活動則通過複數、超複數或矩陣運算來呈現幾何的變換。這種教學視角與古典幾何形成鮮明對比，當學生後續接觸解析幾何時，坐標旋轉與反射的概念便能快速銜接。所有這些概念都為線性代數中反射概念的拓展做好了準備。

教育工作者們已對其展現出了相當興趣，並且設計了從幼兒園到高中各學段的變換幾何教學方案。針對低齡兒童，為避免引入專業術語並關聯其日常經驗，建議使用"翻轉"指代直線反射，"平移"指代位移，"旋轉"指代轉動儘管這些並非精確的數學語言。部分方案要求學生先操作實體模型，再通過點集映射定義理解抽象的變換^[3]^[4]^[5]。

在推動改革俄羅斯的幾何課程時，柯爾莫哥洛夫主張從變換視角重構課程體系，使幾何教學建立在集合論基礎上。這導致"全等"取代了傳統的"相等"表述：由於圖形被視為點集，它只能與自身相等，而通過等距變換能完全重合的兩個三角形則被稱為全等^[2]。

有位作者如此講述群論對變換幾何的重要性："我刻意從基本原理出發構建了所需的群論體系，意在能使本書作為變換群及抽象群論概念的啟蒙讀本，即使你從未接觸過這些領域"。^[6]

在教學領域的應用

參見

參考資料

延伸閱讀

Wikiwand - on