質數計算函數

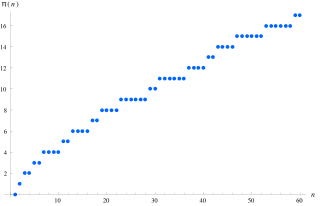
在數學中，質數計數函數是一個用來表示小於或等於某個實數x的質數的個數的函數，記為${\displaystyle \pi (x)}$。

π(n)的最初60個值

歷史

在數論中，質數計數函數的增長率引起了很大的興趣。在18世紀末，高斯和勒壤得曾猜想這個函數大約為：

${\displaystyle x/\operatorname {ln} (x)\!}$

也就是

${\displaystyle \lim _{x\rightarrow \infty }{\frac {\pi (x)}{x/\operatorname {ln} (x)}}=1.\!}$

這就是質數定理。一個等價的表述，是：

${\displaystyle \lim _{x\rightarrow \infty }\pi (x)/\operatorname {li} (x)=1\!}$

其中${\displaystyle \operatorname {li} (x)}$是對數積分函數。這個定理在1896年由法國數學家雅克·阿達馬和比利時數學家德·拉·瓦萊布桑先後獨立給出證明。證明用到了黎曼ζ函數的性質。

目前已知${\displaystyle \pi (x)\!}$還有更精確的估計，例如：

${\displaystyle \pi (x)=\operatorname {li} (x)+\mathrm {O} \left(x\exp \left(-{\frac {\sqrt {\ln(x)}}{15}}\right)\right)\!}$

其中O是大O符號。1948年，阿特勒·塞爾伯格和保羅·艾狄胥不使用函數或複分析證明了質數定理。

另外一個關於質數計數函數的增長率的猜想，是：

${\displaystyle \sum _{p\leq x}p^{n}\sim \pi (x^{n+1})\sim Li(x^{n+1}).}$

π(x)、x / ln x和li(x)

x	π(x)	π(x) − x / ln x	li(x) − π(x)	x / π(x)	x / ln x  % Error
10	4	−0.3	2.2	2.500	-7.5%
102	25	3.3	5.1	4.000	13.20%
103	168	23	10	5.952	13.69%
104	1,229	143	17	8.137	11.64%
105	9,592	906	38	10.425	9.45%
106	78,498	6,116	130	12.740	7.79%
107	664,579	44,158	339	15.047	6.64%
108	5,761,455	332,774	754	17.357	5.78%
109	50,847,534	2,592,592	1,701	19.667	5.10%
1010	455,052,511	20,758,029	3,104	21.975	4.56%
1011	4,118,054,813	169,923,159	11,588	24.283	4.13%
1012	37,607,912,018	1,416,705,193	38,263	26.590	3.77%
1013	346,065,536,839	11,992,858,452	108,971	28.896	3.47%
1014	3,204,941,750,802	102,838,308,636	314,890	31.202	3.21%
1015	29,844,570,422,669	891,604,962,452	1,052,619	33.507	2.99%
1016	279,238,341,033,925	7,804,289,844,393	3,214,632	35.812	2.79%
1017	2,623,557,157,654,233	68,883,734,693,281	7,956,589	38.116	2.63%
1018	24,739,954,287,740,860	612,483,070,893,536	21,949,555	40.420	2.48%
1019	234,057,667,276,344,607	5,481,624,169,369,960	99,877,775	42.725	2.34%
1020	2,220,819,602,560,918,840	49,347,193,044,659,701	222,744,644	45.028	2.22%
1021	21,127,269,486,018,731,928	446,579,871,578,168,707	597,394,254	47.332	2.11%
1022	201,467,286,689,315,906,290	4,060,704,006,019,620,994	1,932,355,208	49.636	2.02%
1023	1,925,320,391,606,803,968,923	37,083,513,766,578,631,309	7,250,186,216	51.939	1.93%
1024	18,435,599,767,349,200,867,866	339,996,354,713,708,049,069	17,146,907,278	54.243	1.84%
1025	176,846,309,399,143,769,411,680	3,128,516,637,843,038,351,228	55,160,980,939	56.546	1.77%
1026	1,699,246,750,872,437,141,327,603	28,883,358,936,853,188,823,261	155,891,678,121	58.850	1.70%
1027	16,352,460,426,841,680,446,427,399	267,479,615,610,131,274,163,365	508,666,658,006	61.153	1.64%

計算π(x)的方法

如果${\displaystyle x}$不太大，一個簡單的計算${\displaystyle \pi (x)}$的方法就是算出每個質數（比如使用愛拉托散尼篩法）。

一個比較複雜的計算${\displaystyle \pi (x)}$的方法是勒壤得發現的：給定${\displaystyle x}$，如果${\displaystyle p_{1}}$、 ${\displaystyle p_{2}}$、 ……、 ${\displaystyle p_{k}}$是不同的質數，則小於${\displaystyle x}$且不能被任何一個${\displaystyle p_{i}}$整除的整數個數是：

${\displaystyle \lfloor x\rfloor -\sum _{i}\left\lfloor {\frac {x}{p_{i}}}\right\rfloor +\sum _{i<j}\left\lfloor {\frac {x}{p_{i}p_{j}}}\right\rfloor -\sum _{i<j<k}\left\lfloor {\frac {x}{p_{i}p_{j}p_{k}}}\right\rfloor +\cdots ,}$

（其中${\displaystyle \lfloor \cdot \rfloor }$是取整函數）。因此這個數等於：

${\displaystyle \pi (x)-\pi \left({\sqrt {x}}\right)+1\,}$

其中${\displaystyle p_{1},p_{2},\dots ,p_{k}}$是小於或等於${\displaystyle x}$的平方根的質數。

恩斯特·梅塞爾在1870年和1885年發表的一系列文章中，描述並使用了一個計算${\displaystyle \pi (x)}$的組合方法。設${\displaystyle p_{1}}$, ${\displaystyle p_{2}}$, …, ${\displaystyle p_{n}}$是最初${\displaystyle n}$個質數，將不大於${\displaystyle m}$且不被任何${\displaystyle p_{i}}$整除的自然數個數記為${\displaystyle \Phi (m,n)}$，那麼：

${\displaystyle \Phi (m,n)=\Phi (m,n-1)-\Phi \left(\left[{\frac {m}{p_{n}}}\right],n-1\right).\,}$

給定一個自然數${\displaystyle m}$，如果${\displaystyle n=\pi \left({\sqrt[{3}]{m}}\right)}$且${\displaystyle \mu =\pi \left({\sqrt {m}}\right)-n}$，那麼：

${\displaystyle \pi (m)=\Phi (m,n)+n(\mu +1)+{\frac {\mu ^{2}-\mu }{2}}-1-\sum _{k=1}^{\mu }\pi \left({\frac {m}{p_{n+k}}}\right).\,}$

利用這種方法，梅塞爾計算了${\displaystyle x}$等於5×10⁵、10⁶、10⁷以及10⁸時${\displaystyle \pi (x)}$的值。

1959年，德里克·亨利·勒梅爾推廣並簡化了梅塞爾的方法。對於實數${\displaystyle m}$和自然數${\displaystyle n}$和${\displaystyle k}$，定義${\displaystyle P_{k}(m,n)}$為不大於m且正好有k個大於${\displaystyle p_{n}}$的質因子的整數個數。更進一步，設定${\displaystyle P_{0}(m,n)=1}$。那麼：

${\displaystyle \Phi (m,n)=\sum _{k=0}^{+\infty }P_{k}(m,n),\,}$

這個和實際上只有有限個非零的項。設${\displaystyle y}$為一個整數，使得${\displaystyle {\sqrt[{3}]{m}}\leq y\leq {\sqrt {m}}}$，並設${\displaystyle n=\pi (y)}$。那麼當${\displaystyle k}$ ≥ 3時，${\displaystyle P_{1}(m,n)=\pi (m)-n}$且${\displaystyle P_{k}(m,n)=0}$。因此：

${\displaystyle \pi (m)=\Phi (m,n)+n-1-P_{2}(m,n).}$

${\displaystyle P_{2}(m,n)}$的計算可以用這種方法來獲得：

${\displaystyle P_{2}(m,n)=\sum _{y<p\leq {\sqrt {m}}}\left(\pi \left({\frac {m}{p}}\right)-\pi (p)+1\right).\,}$

另一方面，${\displaystyle \Phi (m,n)}$的計算可以用以下規則來完成：

1. ${\displaystyle \Phi (m,0)=\lfloor m\rfloor ;\,}$
2. ${\displaystyle \Phi (m,b)=\Phi (m,b-1)-\Phi \left({\frac {m}{p_{b}}},b-1\right).\,}$

利用這種方法，勒梅爾計算了${\displaystyle \pi \left(10^{10}\right)}$。

其它質數計數函數

我們也使用其它的質數計數函數，因為它們更方便。其中一個是黎曼的質數計數函數，通常記為${\displaystyle \Pi _{0}(x)}$。這個函數在自變量為質數的冪pⁿ時突然增加了1/n，而該點的值則是兩邊的平均值。我們可以用以下公式來定義${\displaystyle \Pi _{0}(x)}$：

${\displaystyle \Pi _{0}(x)={\frac {1}{2}}{\bigg (}\sum _{p^{n}<x}{\frac {1}{n}}\ +\sum _{p^{n}\leq x}{\frac {1}{n}}{\bigg )}}$

其中p是質數。

也可以寫成以下公式：

${\displaystyle \Pi _{0}(x)=\sum _{2}^{x}{\frac {\Lambda (n)}{\ln n}}-{\frac {1}{2}}{\frac {\Lambda (x)}{\ln x}}=\sum _{n=1}^{\infty }{\frac {1}{n}}\pi _{0}(x^{1/n})}$

其中Λ(n)是馮·曼戈爾特函數，

${\displaystyle \pi _{0}(x)=\lim _{\varepsilon \rightarrow 0}{\frac {\pi (x-\varepsilon )+\pi (x+\varepsilon )}{2}}.}$

利用默比烏斯反演公式，可得：

${\displaystyle \pi _{0}(x)=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n}}\Pi _{0}(x^{1/n})}$

知道了黎曼ζ函數的對數與馮·曼戈爾特函數${\displaystyle \Lambda }$之間的關係，並利用佩龍公式，可得：

${\displaystyle \ln \zeta (s)=s\int _{0}^{\infty }\Pi _{0}(x)x^{-s+1}\,dx}$

不等式

下面是一些有用的π(x)不等式。

${\displaystyle {\frac {x}{\ln x}}<\pi (x)<1.25506{\frac {x}{\ln x}}\!}$，左不等式適用於x ≥ 17，右不等式適用於x>1，常數1.25506為 ${\displaystyle {\frac {30\ln 113}{113}}}$保留5位有效小數，${\displaystyle {\frac {\pi (x)\ln x}{x}}}$最大值為x = 113。

Pierre Dusart 在2010年證明：

${\displaystyle {\frac {x}{\ln x-1}}<\pi (x)\!}$ （其中${\displaystyle x\geq 5393}$）

${\displaystyle \pi (x)<{\frac {x}{\ln x-1.1}}\!}$ （其中${\displaystyle x\geq 60184}$）

第n個質數p_n的不等式：

${\displaystyle n\ln n+n\ln \ln n-n<p_{n}<n\ln n+n\ln \ln n\!}$

左面的不等式當n ≥ 2時成立，右面的不等式當n ≥ 6時成立，上限由Rosser（1941）提出，下限由Dusrat（1999）提出。

第n個質數的一個估計是：

${\displaystyle p_{n}=n\ln n+n\ln \ln n-n+{\frac {n\ln \ln n-2n}{\ln n}}+O\left({\frac {n(\ln \ln n)^{2}}{(\ln n)^{2}}}\right).}$

參考文獻

• Bach, Eric; Shallit, Jeffrey. Algorithmic Number Theory. MIT Press. 1996: volume 1 page 234 section 8.8. ISBN 0-262-02405-5. 引文使用過時參數coauthors (幫助)

• Marc Deléglise and Jöel Rivat, Computing ${\displaystyle \pi (x)}$: The Meissel, Lehmer, Lagarias, Miller, Odlyzko method（頁面存檔備份，存於互聯網檔案館）, Mathematics of Computation, vol. 65, number 33, January 1996, pages 235–245

• Dickson, Leonard Eugene. History of the Theory of Numbers I: Divisibility and Primality. Dover Publications. 2005. ISBN 0-486-44232-2.

• Ireland, Kenneth; Rosen, Michael. A Classical Introduction to Modern Number Theory Second edition. Springer. 1998. ISBN 0-387-97329-X. 引文使用過時參數coauthors (幫助) 引文格式1維護：冗餘文本 (link)

• 埃里克·韋斯坦因. Riemann Prime Counting Function. MathWorld.

• Hwang H. Cheng Prime Magic conference given at the University of Bordeaux (France) at year 2001 Démarches de la Géométrie et des Nombres de l'Université du Bordeaux

• Titchmarsh, E. C. The Theory of Functions, 2nd ed. Oxford, England: Oxford University Press, 1960.

• Oliveira e Silva, Tomás Tables of values of pi(x) and of pi2(x) （頁面存檔備份，存於互聯網檔案館）

• Gourdon, Xavier; Sebah,Pascal PrimePi values thru 4E22（頁面存檔備份，存於互聯網檔案館）