
动力系统
维基百科,自由的 encyclopedia
数学中,动力系统(dynamical system)是用函数描述环绕空间中某点随时间的变化情况的系统,例如描述钟摆晃动、管道中水的流动,或者湖中每年春季鱼类的数量,凡此等等的数学模型都是动力系统。对时空测量的不同选择中,最一般的定义统一了数学中的数个概念,如常微分方程和遍历理论。[来源请求]时间可用整数、实数或复数甚至更一般的代数对象来度量;空间可以是流形,也可以是集合,无需在其上定义光滑的时空结构。
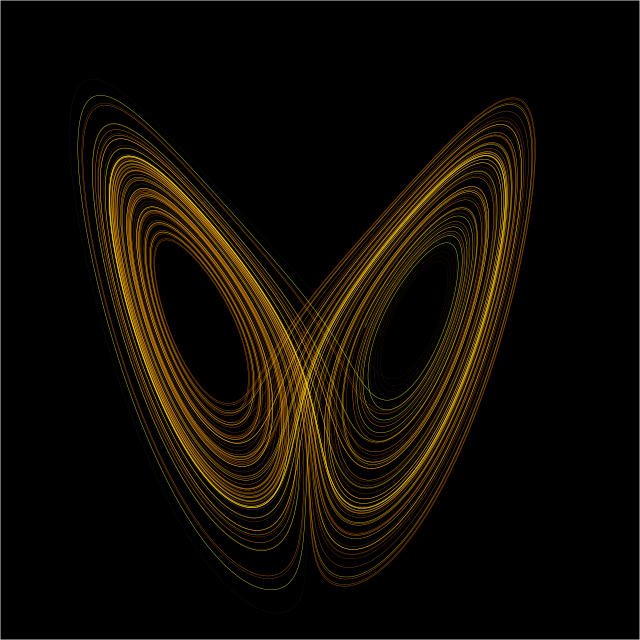
在动力系统中有所谓状态的概念,是一组可确定的实数。这组实数也是一种流形的几何空间坐标。动力系统的演化规则是一组函数的固定规律,描述了当前状态会如何产生未来状态。这种规则是确定的,即对于给定的时间间隔内,从现在的状态只能演化出一个未来的状态。[1][2]不过也有随机的系统,因为随机事件也会影响状态变量的演化。
若只是在一系列不连续的时间点考察系统的状态,则这个动力系统为离散动力系统;若时间连续,就得到一个连续动力系统。如果系统以一种连续可微的方式依赖于时间,我们就称它为一个光滑动力系统。 物理学中的动力系统被描述为“状态随时间变化,并因此服从涉及时间导数的微分方程的粒子(群)”。[3]要预测系统未来的行为,需要通过计算机模拟实现这些方程式的分析求解或随时间积分。
对动力系统的研究是动力系统理论的重点,其在数学、物理学、[4][5]生物学、[6]化学、工程学、[7]经济学、[8]历史学和医学等众多领域都有应用。动力系统是混沌理论、逻辑斯谛映射动力学、分岔理论、自组装和自组织过程与混沌边缘概念的基本组成。