
平面波
维基百科,自由的 encyclopedia
在三维空间里,平面波(plane wave)是一种波动,其波阵面(在任何时刻,波相位相等的每一点所形成的曲面)是相互平行的平面。平面波的传播方向垂直于波前。假若平面波的振幅不是常数,例如,振幅是位置的函数,则称此种平面波为“非均匀平面波”。[1]:24-27
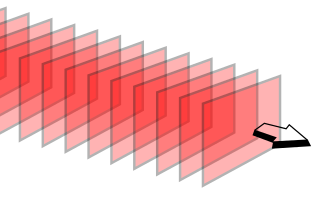
加以延伸,平面波这术语时常用来形容,在空间的一个局部区域里,近似于平面波的波动。例如,一个局部区域波源,像发射无线电波的天线,所发射出的电磁波,在远场区(英语:far-field region)可以近似为平面波。等价地说,对于在一个均匀介质内,波的传播距离超长于波长的案例,在几何光学的正确极限内,射线区域性地对应于近似平面波。

