乘法

乘法（英语、法语：multiplication）是四则运算之一。乘法运算的本质，就是​​“同类累加的简写形式​​”。

3×4 = 12

例如：

${\displaystyle a\times b=\underbrace {b+\cdots +b} _{a{\text{ 个 b}}}.}$

${\displaystyle a}$ 和 ${\displaystyle b}$ 都是本式的因数（或称约数），其运算结果称为积。

须注意的是，华人地区有将四则运算的被运算数和运算数统一位置，念作“a 乘以 b”（“a times b”）或“b 乘 a”（“a multiplied by b”）。前者 ${\displaystyle a}$ 是乘数，${\displaystyle b}$ 是被乘数，后者则相反。而乘数和被乘数的交替并不会影响乘法的结果。^[1][2]

乘法运算亦有其它形象理解：对于整数乘法，可表现为将对象排列成矩形数组；对于实数乘法，则可解释为计算矩形面积。同样地，运算结果不受边长测量顺序的影响。

在乘法基本概念的基础上，序列乘积、向量乘法、复数及矩阵运算等均对其进行了概念扩展。这些更高级的数学结构会以各自方式影响乘法的基本性质——例如矩阵乘法和某些向量乘法会呈现非交换性，复数乘法则会改变复数的符号。

引言

首先，进入正题前，我们不妨来看两个生活中的例子：

• 买5个单价为3圆的冰激凌：由${\displaystyle 5\times 3=15}$可得，需要支付15圆。
• 要搭一个3层高、每层4块积木的小塔：由${\displaystyle 3\times 4=12}$可得，需要12块积木。

其次，数学和物理存在许多“累加关系”：

• 已知匀速直线运动状态下，某物体行进速度为 ${\displaystyle v}$ ，所用时间为 ${\displaystyle t}$ ，可得累计距离 ${\displaystyle d=v\times t}$ ；
• 已知一个物体的密度为 ${\displaystyle \rho }$ （假设密度均匀），体积为 ${\displaystyle V}$ ，可得其质量 ${\displaystyle m=\rho \times V}$ ；

......

可见，在数学，尤其是在基本算术中，乘法是​​加法的“快捷版”​​。

定义

基本定义

乘法运算，指通过特定法则将两个或多个数结合生成积的运算过程。其核心内涵包括：

1. 同类累加的简写形式：表示将相同值的数进行连续叠加的运算（如 ${\displaystyle 3\times 4=4+4+4=12}$ ）
2. 比例关系的量化表达：当乘数非整数时，可表示为原数的分数（小数）倍（如 ${\displaystyle 3\times 0.5}$ 表示 ${\displaystyle 3}$ 的一半，${\displaystyle 4\times {\dfrac {1}{3}}}$ 表示 ${\displaystyle 4}$ 的三分之一）
3. 维度扩展的数学工具：在几何学中，用于计算面积（长 ${\displaystyle \times }$ 宽）、体积（长 ${\displaystyle \times }$ 宽 ${\displaystyle \times }$ 高）等空间度量

符号与表示

主条目：乘号

乘法可以用几种方法表示。以下的式子表示“五乘以二”：

• ${\displaystyle 5\times 2}$
• ${\displaystyle 5\cdot 2}$
• ${\displaystyle 5*2}$
• ${\displaystyle (5)(2)}$

古代常用的方法是将两个数并排，没有什么特别的符号来表示乘法。

以“${\displaystyle \times }$”表示乘法，是由奥特雷德于1618年最先引入，也是现在最流行的写法。在电脑领域，也有为方便键盘输入而以小写英文字母“x”替代“×”。

以“${\displaystyle \cdot }$”表示乘法，如今已成为美国^[3][4]、德国、法国等国家^[5]的标准。其最早由托马斯·哈里奥特于1631年出版的著作使用，但令这种用法影响深远的人是莱布尼兹。

因为星号“${\displaystyle *}$”是键盘必备的符号，电脑常用其表示乘号，这种用法起源于FORTRAN语言。

代数中，为方便书写，乘号常被略去（如 ${\displaystyle 5x}$ 和 ${\displaystyle xy}$ ）。但如果变量多于一个字母，则易令人混淆。同时如果只有数字，乘号则不应略去，如 ${\displaystyle 5\times 2}$ 不会表示成 ${\displaystyle 52}$ 。

累乘则用大写希腊字母 ${\displaystyle \Pi }$（Pi）表示：

${\displaystyle \prod _{i=m}^{n}x_{i}:=x_{m}\cdot x_{m+1}\cdot x_{m+2}\cdot \ldots \cdot x_{n-1}\cdot x_{n}}$

性质

乘法运算的数学性质在不同定义和数系下具有多样性，以下是主要分类及详细说明。

基本运算律

1. 交换律：${\displaystyle xy=yx}$
2. 结合律：${\displaystyle (xy)z=x(yz)}$
3. 分配律：${\displaystyle x(y+z)=xy+xz}$

单位元、零元与逆元性质​

1. 乘法单位律：任何数乘以 ${\displaystyle 1}$ ，都会等于该数本身，即${\displaystyle 1x=x}$。此律可扩展至多项式中的常数项。
2. 零元性质：任何数乘以 ${\displaystyle 0}$ ，即是什么也没做过，结果为零，即${\displaystyle 0x=0}$。同样地，多个约数中若含 ${\displaystyle 0}$ ，积必为 ${\displaystyle 0}$ 。
3. 逆元性质：非零数 ${\displaystyle a}$ 的逆元（亦为其倒数）为 ${\displaystyle {\dfrac {1}{a}}}$ ，满足 ${\displaystyle a\times {\dfrac {1}{a}}=1}$ 。

特殊数系下的性质​

实数与复数除法

1. 满足交换律、结合律、分配律。
2. 复数乘法涉及模长和辐角的变化。

矩阵乘法

1. 满足结合律和分配律，但​​不满足交换律，特殊矩阵（如对角矩阵）除外。
2. 对零矩阵：所有元素为 ${\displaystyle 0}$ 的矩阵，与任意矩阵相乘结果为零矩阵。

模运算

在模 ${\displaystyle n}$ 下，乘法逆元存在当且仅当数与 ${\displaystyle n}$ 互素（如模素数时所有非零数均有逆元）。

不同的乘法运算

两个数的乘法运算或积（这两个数可以是自然数、整数、分数、实数、复数、四元数等）的数学定义，相似而又各有特性。

自然数乘法

两个自然数 ${\displaystyle m,n\in \mathbb {N} }$ ，其乘积为：

${\displaystyle mn=nm=\sum _{k=1}^{n}m=\sum _{k=1}^{m}n}$

这是将该整数自身重复相加若干次的简写法。换言之：

${\displaystyle mn=nm=\underbrace {m+m+m+\cdots +m} _{n{\text{个 m}}}=\underbrace {n+n+n+\cdots +n} _{m{\text{个 n}}}}$

长远来看，将乘法视为重复加法并不高效。因此，数学家归纳了从 ${\displaystyle 1}$ 到 ${\displaystyle 9}$ 的乘法结果，即九九乘法表。

多个自然数相乘时，我们使用括号标明运算顺序。为避免过多括号，规定以下优先级规则：乘法始终优先于加法。例如在表达式 ${\displaystyle 4+5\times 2}$ 中，应理解为 ${\displaystyle 4+(5\times 2)=4+10=14}$ ，而非 ${\displaystyle (4+5)\times 2=9\times 2=18}$ 。

当${\displaystyle x}$是量，${\displaystyle y}$是自然数时，定义乘法递归如下：

${\displaystyle 0x=0}$

${\displaystyle xy=x+x(y-1)}$

整数乘法

图中，笛卡儿坐标系的蓝色区域表示乘积为正，红色区域表示乘积为负。

在数轴上表示整数乘法时，可借助向量的方向与长度直观理解

整数乘法推广自然数乘法至负数，符号规则为：同号得正，异号得负，绝对值相乘。

分数（小数）乘法

两个分数 ${\displaystyle {\frac {z}{n}},{\frac {z'}{n'}}}$ 作乘法运算时，分子与分子相乘，分母与分母相乘：

${\displaystyle {\frac {z}{n}}\cdot {\frac {z'}{n'}}={\frac {z\cdot z'}{n\cdot n'}}}$

当且仅当 ${\displaystyle n,n'\neq 0}$ 时成立。

两个小数作乘法运算时，可利用乘法交换律的特性进行计算。

例如，计算 ${\displaystyle 43.1}$ 乘以 ${\displaystyle 1.215}$ 时：

${\displaystyle {\begin{aligned}43.1\times 1.215&=\left(431\times {\frac {1}{10}}\right)\times \left(1\;215\times {\frac {1}{1\;000}}\right)\\&=(431\times 1\;215)\times \left({\frac {1}{10}}\times {\frac {1}{1\;000}}\right)\\&=(431\times 1\;215)\times {\frac {1}{10\;000}}\\&={\frac {523\;665}{10\;000}}\\&=52.3665\end{aligned}}}$

可见，两个小数作乘法运算时，先忽略小数点，计算两数小数点后数字的位数之和，将两数视为整数相乘，最后在结果中从右往左数出与总位数相同的位数，并放置小数点。

又如，计算 ${\displaystyle 3.15}$ 乘以 ${\displaystyle 1.2}$ 时：

1. 先计算整数部分相乘：${\displaystyle 315\times 12=3780}$
2. 再将小数点向左移动 ${\displaystyle 3}$ 位：${\displaystyle 3780\Rightarrow 3.780}$（末尾的 ${\displaystyle 0}$ 可省略，写作 ${\displaystyle 3.78}$）

实数乘法

实数乘法是前文乘法的推广，性质也相同。其核心在于：每个实数都是某有理数集的上确界。特别地，每个正实数是其无限小数展开式截断序列的上确界，例如 ${\displaystyle \pi }$ 是集合 ${\displaystyle \{3,\;3.1,\;3.14,\;3.141,\ldots \}}$ 的上确界。

实数的一个基本性质是：有理逼近与算术运算（特别是乘法）兼容。这意味着，若正实数 ${\displaystyle a}$ 和 ${\displaystyle b}$ 分别表示为集合 ${\displaystyle A}$ 和 ${\displaystyle B}$ 的上确界（即 ${\displaystyle a=\sup _{x\in A}x}$ ， ${\displaystyle b=\sup _{y\in B}y}$ ），则两数乘积 ${\displaystyle a\cdot b}$ 等于所有 ${\displaystyle x\in A}$ 与 ${\displaystyle y\in B}$ 的乘积项的上确界（即 ${\displaystyle a\cdot b=\sup _{x\in A,y\in B}x\cdot y}$ ）。具体而言，两个正实数的乘积等于其十进制展开式逐项积序列的上确界。

对于涉及负实数的乘法运算，可通过符号法则简化处理：正负号的变化将上确界转化为下确界。很多人都通过柯西序列构造实数，因为这种方法无需考虑四种可能的符号组合情况，从而简化了运算规则的推导过程。

复数乘法

复数乘法可通过分配律和虚数单位性质 ${\displaystyle i^{2}=-1}$ 进行运算。具体地，两个复数 ${\displaystyle (a+b\,i)}$ 与 ${\displaystyle (c+d\,i)}$ 作乘法运算时，展开过程为：

${\displaystyle {\begin{aligned}(a+b\,i)\cdot (c+d\,i)&=a\cdot c+a\cdot d\,i+b\,i\cdot c+b\cdot d\cdot i^{2}\\&=(a\cdot c-b\cdot d)+(a\cdot d+b\cdot c)\,i\end{aligned}}}$

其中 ${\displaystyle i^{2}}$ 替换为 ${\displaystyle -1}$ 后，实部与虚部分别合并。

用极坐标系表示复数

从几何视角理解，复数可表示为极坐标形式：

${\displaystyle a+b\,i=r\cdot (\cos(\varphi )+i\sin(\varphi ))=r\cdot e^{i\varphi }}$

${\displaystyle c+d\,i=s\cdot (\cos(\psi )+i\sin(\psi ))=s\cdot e^{i\psi }}$

此时，复数乘法可转化为模长与辐角的运算：

${\displaystyle (a\cdot c-b\cdot d)+(a\cdot d+b\cdot c)i=r\cdot s\cdot e^{i(\varphi +\psi )}.}$

其几何意义在于模长相乘（ ${\displaystyle r\cdot s}$ ）、辐角相加（ ${\displaystyle \varphi +\psi }$ ）。

四元数乘法

参见：四元数 § 加、乘和一般函数

基于集合论的乘法

非负整数的乘法可通过集合论中的基数概念或皮亚诺公理进行定义。基数理论通过集合的势（即集合元素的数量）定义乘法，例如，两个有限集合的笛卡儿积的势等于各自势的乘积。而皮亚诺公理体系则通过自然数的递归定义实现乘法运算：设非负整数表示为自然数，其乘法可归纳定义为：

• ​​基例​​：对任意非负整数 ${\displaystyle a}$ ，有 ${\displaystyle a\times 0=0}$ ；
• 递推规则​​：对任意非负整数 ${\displaystyle a}$ 、${\displaystyle b}$ ，有 ${\displaystyle a\times {(b+1)}=a\times b+a}$ 。

此定义通过数学归纳法可证明满足乘法结合律、交换律等基本性质。

对于任意整数的乘法，需在自然数乘法基础上引入符号规则。例如，负整数乘法定义为：若 ${\displaystyle a}$ 、${\displaystyle b}$ 为自然数，则 ${\displaystyle {(-a)}\times {(-b)}=a\times b}$ ，而 ${\displaystyle {(-a)}\times b=-{(a\times b)}}$ 。这一扩展保持了乘法运算的代数结构一致性。

有理数乘法则通过分数形式定义：若 ${\displaystyle {\dfrac {a}{b}}}$ 与 ${\displaystyle {\dfrac {c}{d}}}$ 为最简分数（ ${\displaystyle b}$ 、${\displaystyle d\neq 0}$ ），则其乘积为 ${\displaystyle {\dfrac {ac}{bd}}}$ ，分母通过集合论中的笛卡尔积构造，分子通过自然数乘法定义。此过程需验证运算的封闭性与唯一性，例如通过交叉相乘消去公约数，确保结果仍为最简分数。

实数乘法的定义依赖于有理数乘法的完备性。通过戴德金分割或柯西序列构造实数时，乘法运算被定义为极限运算：若 ${\displaystyle \{a_{n}\}}$ 和 ${\displaystyle \{b_{n}\}}$ 为收敛的有理数序列，则实数乘积定义为 ${\displaystyle \lim(a_{n}\times b_{n})}$ 。此定义需满足乘法与极限运算的交换性，并通过 ${\displaystyle \epsilon -\delta }$ 语言严格证明其合理性。

基于群论的乘法

在群论中，若一个集合在乘法运算下满足封闭性、结合律、存在单位元且每个元素均有逆元素，则称其构成群结构。这些公理构成了群的定义基础。

以非零有理数集为例，其乘法运算满足群的所有条件：单位元为1（不同于加法群的单位元0），每个非零有理数均存在乘法逆元，且乘法运算封闭（因为两个非零有理数相乘仍为非零有理数）。但需注意的是，零必须被排除，因其乘法逆元不存在。此例中的群为阿贝尔群，但群论中并非所有乘法群均为阿贝尔群。

考虑可逆方阵群：给定域上同维数的可逆矩阵集合，其乘法运算满足封闭性（矩阵相乘仍为同维可逆矩阵）、结合律、单位矩阵作为单位元，且每个矩阵均有逆矩阵。然而，矩阵乘法不满足交换律（如 ${\displaystyle {AB}\neq {BA}}$ ），因此该群为非阿贝尔群。

即使排除零元，整数集在乘法下也不构成群。原因在于除 ${\displaystyle 1}$ 和 ${\displaystyle -1}$ 外，其他整数均无乘法逆元。这一特性凸显了乘法群对逆元存在与否的严格要求。

群的乘号通常表示为点乘（${\displaystyle \cdot }$）或直接省略不写。在描述群时，点乘符号常用于明确运算，例如非零有理数乘法群可记为（ ${\displaystyle \mathbb {Q} \{0\},\cdot }$ ）。这种符号体系与加法群（如（ ${\displaystyle \mathbb {Z} ,+}$ ））形成对比，体现了运算类型的差异。

运算方法

历史上的算法

迄今为止发现的最早的乘法运算，是可追溯至旧石器时代初期的伊尚戈骨上的刻痕。划痕可能是计数符号，也可能只是为了方便抓握，或有其他非数学的目的。^[6]

古埃及人采用连续加倍法进行整数和分数的乘法运算，这一方法在《莱因德数学纸草书》中有详细记载。^[7]例如，计算 ${\displaystyle 13\times 21}$ 时，通过将${\displaystyle 21}$依次加倍三次得到${\displaystyle 42}$、${\displaystyle 84}$、${\displaystyle 168}$，再根据加倍序列中的对应项，得出 ${\displaystyle {(1+4+8)}\times 21=273}$ 。

巴比伦人使用六十进制系统，其乘法运算与现代十进制类似，但因 ${\displaystyle 60\times 60=3600}$ 种组合过多，他们通过制作包含前${\displaystyle 20}$个基数倍数的乘法表（如 ${\displaystyle n,2n,\ldots ,20n}$ 及 ${\displaystyle 30n,40n,50n}$ ）来简化计算，如 ${\displaystyle 53n}$ 可通过 ${\displaystyle 50n+3n}$ 的组合快速得出。

古希腊人以几何图形（如矩形）表示乘法，体现“乘积即面积”的思想。欧几里得更是在《几何原本》中用几何方法证明乘法分配律。

孙子筹算乘法

中国古代拥有史上最早、最详细的​​十进制位值制​​乘法规则，其首见于南北朝时期的孙子算经。孙子乘法的核心，是通过纵横排列的算筹模拟位值运算，如计算 ${\displaystyle 49\times 36}$ 时，先以算筹摆出 ${\displaystyle 49}$ 和 ${\displaystyle 36}$ ，再按“九九表”逐位相乘并累加，终得 ${\displaystyle 1764}$ 。这种算法在9世纪传至中东，13世纪又译成拉丁文而流行于欧洲。至于九九乘法表​​，则在战国时期已成熟应用^[8]，其采用“小九九”形式，从“九九八十一”到“一一如一”，比古埃及的累加法效率提升数十倍。

阿拉伯穆斯林于9世纪引入印度数字和位值制，结合阿拉伯语符号形成计算体系，推动乘法运算标准化。而数学家花拉子米在接纳中国的孙子乘法后，在《代数学》中将乘法与方程系统化结合，提出“还原与对消”法，将乘法纳入代数运算框架，影响欧洲数学发展。

印度类似“铺地锦”的图形化乘法

纳皮尔的骨头

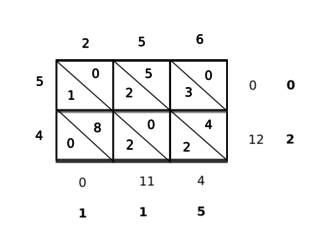
印度古代的乘法运算亦有发展。7世纪，数学家婆罗摩笈多提出“交叉相乘法”，即 ${\displaystyle (a+b)(c+d)=ac+ad+bc+bd}$ ，简化多位数乘法步骤。例如计算 ${\displaystyle {123}\times {456}}$ 时，通过分项相乘再求和，减少重复计算。12世纪，印度文献中出现类似中国古代“铺地锦”的图形化乘法，通过网格线段交叉点计数得出结果，后经阿拉伯传入欧洲。“纳皮尔的骨头”便是借鉴“铺地锦”的灵感产生的。

现代算法

现代基于印度-阿拉伯数字系统的乘法，最早同样由婆罗摩笈多系统阐述。他在7世纪著作《婆罗摩修正体系》中完整定义了加、减、乘、除四则运算的规则，其乘法体系包含多种算法，现代竖式乘法即源于此。此算法通过花拉子米的著作《印度数字算术》于9世纪初传入阿拉伯世界，其《代数学》系统集成了印度数字与运算规则。13世纪，意大利数学家斐波那契在《计算之书》中推广此法，最终使印度-阿拉伯数字系统取代罗马数字成为欧洲主流。^[9]

由于历史影响，华人小学生现在仍背诵九九乘法表来学习乘法。

关于电脑的特别算法，以及其它现代运算法，详见乘法算法。

其它算法

用手指算乘法

除了加法，在有限范围内，乘法也可以用手指完成。为此，两个约数需处于同一十位半区，也就是说，两者要么均以 ${\displaystyle 1}$ 至 ${\displaystyle 5}$ 结尾，要么均以 ${\displaystyle 6}$ 至 ${\displaystyle 0}$ 结尾。

对于因数以 ${\displaystyle 1}$ 至 ${\displaystyle 5}$ 结尾的情况：

1. 首先为手指编号：从小指开始，依次标记为 ${\displaystyle 10\cdot {(d-1)}+1}$ 至拇指为 ${\displaystyle 10\cdot {(d-1)}+5}$ （其中 ${\displaystyle d}$ 表示对应数的十位，如第二位为 ${\displaystyle 1}$ 时，对应 ${\displaystyle 11}$ 至 ${\displaystyle 15}$ ）；
2. 对齐两个因数的手指后，数出下方手指总数（包括对齐的手指），将其乘以 ${\displaystyle d\cdot 10}$ ；
3. 计算左右手下方手指（不包含对齐的手指）的乘积；
4. 最后，加上常数项 ${\displaystyle {d^{2}}\cdot 100}$ ，结果即为所求。

对于因数以 ${\displaystyle 6}$ 至 ${\displaystyle 0}$ 结尾的情况：

1. 类似地，从小指开始，依次标记为 ${\displaystyle 10\cdot {(d-1)}+6}$ 至拇指为 ${\displaystyle 10\cdot d}$ （其中 ${\displaystyle d}$ 表示对应数的十位，如第二位为 ${\displaystyle 1}$ 时，对应 ${\displaystyle 16}$ 至 ${\displaystyle 20}$ ）；
2. 对齐两个因数的手指后，数出下方手指总数（包括对齐的手指），将其乘以 ${\displaystyle d\cdot 10}$ （同上）；
3. 计算左右手上方手指（不包含对齐的手指）的乘积（同上）；
4. 最后，加上常数项 ${\displaystyle d\cdot {(d-1)}\cdot 100}$ ，结果即为所求。

以 ${\displaystyle 7\times 8}$ 为例： ${\displaystyle 7}$ 和 ${\displaystyle 8}$ 均以 ${\displaystyle 6}$ 至 ${\displaystyle 0}$ 结尾，而 ${\displaystyle d=1}$ 。对齐手指后，下方手指有 ${\displaystyle 5}$ 根，乘以 ${\displaystyle 1\times 10=10}$ 得 ${\displaystyle 50}$ ；上方手指分别为 ${\displaystyle 3}$ 根和 ${\displaystyle 2}$ 根，积为 ${\displaystyle 3\times 2=6}$ ；加法常数项 ${\displaystyle {(1-1)}\cdot 1\cdot 100=0}$，总和为 ${\displaystyle 50+6+0=56}$ 。

再如 ${\displaystyle 24\times 22}$ ： ${\displaystyle 24}$ 和 ${\displaystyle 22}$ 均以 ${\displaystyle 1}$ 至 ${\displaystyle 5}$ 结尾，而 ${\displaystyle d=2}$ 。对齐手指后，下方手指有 ${\displaystyle 6}$ 根，乘以 ${\displaystyle 2\times 10=20}$ 得到 ${\displaystyle 120}$ ；下方手指分别为 ${\displaystyle 4}$ 根和 ${\displaystyle 2}$ 根，积为 ${\displaystyle 4\times 2=8}$ ；加法常数项 ${\displaystyle {2^{2}}\cdot 100=400}$ ，总和为 ${\displaystyle 120+8+400=528}$ 。

此方法尤其适用于快速心算平方数。对于不同十位或十位半区的因数，可通过分解为和的形式（如 ${\displaystyle {(a+x)}\cdot {(a+y)}}$ ）应用该技巧。其数学原理基于多项式展开：

${\displaystyle (a+x)\cdot (a+y)=a^{2}+(x+y)\cdot a+x\cdot y}$

尺规作图法

从相交弦定理出发的尺规法

图1
利用相交弦定理算乘法

如图1所示，过点 ${\displaystyle O}$ 作一直线，分别在 ${\displaystyle O}$ 点两侧截取长度为 ${\displaystyle a}$ 和 ${\displaystyle b}$ 的线段，得点 ${\displaystyle A}$ 和 ${\displaystyle B}$ 。再从 ${\displaystyle O}$ 出发，沿另一方向作射线，截取单位长度 ${\displaystyle 1}$ ，得点 ${\displaystyle E}$ 。过 ${\displaystyle A}$ 、${\displaystyle B}$ 、${\displaystyle E}$ 三点作外接圆，该圆与第二条射线的交点 ${\displaystyle C}$ 满足相交弦定理：

${\displaystyle a\cdot b={\overline {OA}}\cdot {\overline {OB}}=\underbrace {\overline {OE}} _{=1}\cdot \,{\overline {OC}}}$

${\displaystyle {\overline {OE}}=1\Longrightarrow {\overline {OC}}=a\cdot b}$

此法通过构造三角形外接圆，将乘法转化为几何长度的投影关系。

从割线定理出发的尺规法

图2
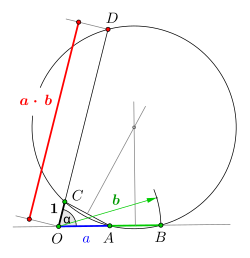
利用割线定理算乘法

如图2所示，设圆外一点 ${\displaystyle O}$ ，沿同一方向截取长度为 ${\displaystyle a}$ 和 ${\displaystyle b}$ 的线段，得点 ${\displaystyle A}$ 和 ${\displaystyle B}$ 。过 ${\displaystyle O}$ 作与 ${\displaystyle BO}$ 成任意角 ${\displaystyle \alpha }$ 的射线，在该射线上截取单位长度 ${\displaystyle 1}$ ，得点 ${\displaystyle C}$ 。作 ${\displaystyle AB}$ 和 ${\displaystyle AC}$ 的垂直平分线以确定圆心，过 ${\displaystyle A}$ 、 ${\displaystyle B}$ 、 ${\displaystyle C}$ 三点作外接圆，该圆与射线交于点 ${\displaystyle D}$ 。根据割线定理：

${\displaystyle a\cdot b={\overline {OA}}\cdot {\overline {OB}}={\overline {OC}}\cdot \,{\overline {OD}}}$

通过调整射线角度 ${\displaystyle \alpha }$ ，可利用相似三角形关系将乘积转化为圆外一点到交点的距离。

从相似三角形出发的尺规法

图3
利用相似三角形算乘法

如图3所示，在射线 ${\displaystyle A}$ 上截取单位长度 ${\displaystyle 1}$ 和长度 ${\displaystyle b}$ ，得点 ${\displaystyle E}$ 和 ${\displaystyle B}$ ，从 ${\displaystyle E}$ 出发，沿另一方向截取长度 ${\displaystyle a}$ ，得点 ${\displaystyle C}$ 。过 ${\displaystyle C}$ 作与 ${\displaystyle AB}$ 平行的直线，与过 ${\displaystyle A}$ 的射线交于点 ${\displaystyle D}$ 。由相似三角形关系可得：

${\displaystyle {\dfrac {\overline {AB}}{\overline {AC}}}={\dfrac {\overline {BD}}{\overline {BC}}}\Longrightarrow {\overline {BD}}=a\cdot b}$

此法通过构造平行线与相似三角形，将乘法运算转化为几何比例问题。