热门问题
时间线
聊天
视角
五角化十二面体
来自维基百科,自由的百科全书
Remove ads
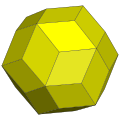
在几何学中,五角化十二面体(Pentakis dodecahedron)是一种六十面体[1],指经过五角化变换的正十二面体[2],换句话说,五角化十二面体是将正十二面体的每个正五边形面替换为五角锥后所形成的立体。当五角锥的锥高恰好使得所形成之立体的所有二面角等角时,则该几何形状是一种卡塔兰立体[3],为截角二十面体的对偶多面体。一般五角化二十面体一词用来称呼卡塔兰立体的版本,即凸多面体的版本,而更高的锥高会使得其成为非凸多面体,例如小星形十二面体[4]。
Remove ads
性质
五角化十二面体由60个面、90条边和32个顶点组成[5],其中60个面皆为全等的等腰三角形组成;在其32个顶点中,其中20个顶点是6个面的公共顶点、12个顶点是5个面的公共顶点[6][7]。由于其具有32个顶点,因此对偶多面体是一个三十二面体,为截角二十面体[8]。五角化十二面体可透过在正十二面体的每个面上叠上锥体构成[9],当其锥高恰好使得所形成之立体的所有二面角等角时,则该几何形状是一种卡塔兰立体[3],在这个情况下,其对应的对偶多面体为一个半正三十二面体。
若将五角化十二面体,五角化变换的原像——正十二面体视为三维类五边形形[10],则五角化十二面体可以视为五边形五边各加一个等腰三角形拼成的正十边形在立体几何中的推广。
五角化十二面体可由正十二面体经过五角化变换来构造。五角化十二面体是将正十二面体的每个正五边形面替换为五角锥后所形成的立体[2]。根据锥高的不同,会使地所构成的立体有不同性质。要确保所构成的立体为严格凸多面体(即没有面两两共面的情况)其加入角锥的锥高不能超过[3]:
其中,为原像多面体的边长。
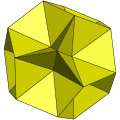
若锥高等于时,所形成的立体将会出现三角形两两共面的情况,若将每个两两共面的三角形是为菱形[9]:167,则所构成的立体为菱形三十面体。[3]更高的锥高将导致所形成的立体变为非凸多面体[9]:167,例如小星形十二面体为加入的锥高为时的情况[4]。
要成为塔卡兰立体,五角化十二面体在五角化的过程必须确保所加入的角锥后的结果所有二面角相等,要达成这个目标所要加入的角锥锥高须为:[3]
Remove ads
作为塔卡兰立体的五角化十二面体,其组成的面为等腰三角形,若腰长为1,则其底边长为[11],对应的底角约为55度41.5分[9]
对应的顶角约为68度37分[9]
应用
部分分子的形状是五角化十二面体,例如Au20Si12[12]。
巴克明斯特富勒烯(C60)分子模型中会形成类似五角化十二面体的外型,其中五角化十二面体的每个面对应着一个碳原子,类似的现象也会出现在石狮子雕塑中的球状物中[13]。等效地,截角二十面体是富勒烯分子模型对应的多面体,每个顶点代表一个碳原子。[14]
部分病毒的外壳模型为五角化十二面体,如腺相关病毒,其包含了60个二十面体对称的衣壳蛋白[15],结合起来构成了五角十二面体的60个对称面。[16]
华特迪士尼世界度假区未来世界的太空船地球号结构是五角化十二面体的细分结果[17]。
变体

当每面叠上的五角锥的高不能使是整个立体的二面角皆相等时,就会有如下情况:
Remove ads
相关多面体
五角化十二面体和三角化二十面体的多角化变换皆可形成菱形三十面体。
参见
参考文献
外部链接
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads
















 ,
,  ...
...