伽利略变换

伽利略变换（英语：Galilean transformation）是经典力学中用以在两个只以匀速相对移动的参考系之间变换的方法，属于一种被动态变换。在相对论效应下，伽利略变换在物体以接近光速运动时不成立^[1]，在电磁系统中也不会成立。^[2]

伽利略·伽利莱在解释匀速运动时制定了这一套概念。^[3]他用其解释球体滚下斜面这一力学问题，并测量出地球表面引力加速度的数值。

在狭义相对论中，伽利略变换被庞加莱变换所取代；相反，庞加莱变换的经典极限c →∞中的群收缩产生了伽利略变换。

平移

伽利略变换示意图

伽利略变换建基于人们加减物体速度的直觉。在其核心，伽利略变换假设时间和空间是绝对的。

这项假设在洛伦兹变换中被舍弃，因此就算在相对论性速度下，洛伦兹变换也是成立的；而伽利略变换则是洛伦兹变换的低速近似值。

以下为伽利略变换的数学表达式，其中${\displaystyle (x,y,z,t)}$和${\displaystyle (x',y',z',t')}$分别为同一个事件在两个坐标系${\displaystyle S}$和${\displaystyle S'}$中的坐标。两个坐标系以相对匀速运行（速度为${\displaystyle v}$），运行方向为${\displaystyle x}$和${\displaystyle x'}$，原点在时间${\displaystyle t=t'=0}$时重合。 ^{[4] [5] [6] [7]}

${\displaystyle x'=x-vt\,}$

${\displaystyle y'=y\,}$

${\displaystyle z'=z\,}$

${\displaystyle t'=t\,}$

最后一条方程式意味着时间是不受观测者的相对运动影响的。

利用线性代数的术语来说，这种变换是个错切，是矩阵对向量进行变换的一个过程。当参考系只沿着x轴移动时，伽利略变换只作用于两个分量：

${\displaystyle (x',t')=(x,t){\begin{pmatrix}1&0\\-v&1\end{pmatrix}}.}$

虽然在伽利略变换中没有必要用到矩阵表达法，但是用了矩阵就可以和狭义相对论中的变换法进行比较。

三种伽利略变换

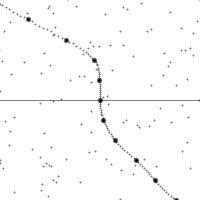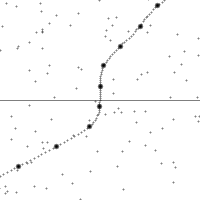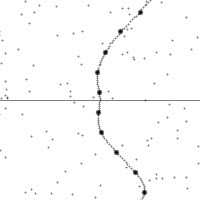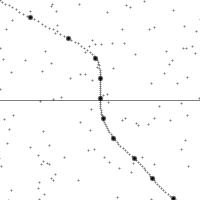
沿着一个加速中观测者的世界线所看到的时空。

纵轴为时间，横轴为距离，虚线为观测者在时空中的轨迹。图的下半部是已经发生了的事件，上半部则是未来的事件。图中小点为时空中的事件。

世界线的斜率为观测者的相对速率。注意观测者在加速时所看到的时空会进行错切。

伽利略变换可以唯一写成由时空的旋转、平移和匀速运动复合而成的函数。^[8]设x为三维空间中的一点，t为一维时间中的一点。时空当中的任何一点可以表达为有序对(x,t)。速度为v的匀速运动表达为${\displaystyle (\mathbf {x} ,t)\mapsto (\mathbf {x} +t\mathbf {v} ,t)}$，其中v在R³内。平移表达为${\displaystyle (\mathbf {x} ,t)\mapsto (\mathbf {x} +\mathbf {a} ,t+b)}$，其中a在R³内，b在R内。旋转表达为${\displaystyle (\mathbf {x} ,t)\mapsto (G\mathbf {x} ,t)}$，其中G : R³ → R³为某正交变换。^[8]作为一个李群，伽利略变换的维度为10。^[8]

这三种变换可更加数学化地表达为伽利略群^[9]。首先G为SO(3)中的旋转矩阵，3维内积在G的作用下保持不变，表达为:${\displaystyle <G{\overrightarrow {x}},G{\overrightarrow {y}}>=<{\overrightarrow {x}},{\overrightarrow {y}}>\,\!}$设在某t时刻有映射${\displaystyle \varphi _{t}({\overrightarrow {a}},{\overrightarrow {b}},G)}$将空间上的某一点x映射到另一点${\displaystyle G{\overrightarrow {x}}+{\overrightarrow {a}}+{\overrightarrow {b}}\cdot t}$上。可证得${\displaystyle \varphi _{t}}$构成一个群。
结合律：${\displaystyle \varphi _{t}}$为线性映射，线性映射满足结合律。

单位元：${\displaystyle \varphi _{t}({\overrightarrow {0}},{\overrightarrow {0}},\mathbf {I} )({\overrightarrow {x}})={\overrightarrow {x}}}$

逆映射：${\displaystyle \varphi _{t}({\overrightarrow {a}},{\overrightarrow {b}},G)^{-1}=\varphi _{t}(-G^{-1}{\overrightarrow {a}},-G^{-1}{\overrightarrow {b}},G^{-1})}$

封闭性：${\displaystyle {\begin{aligned}\varphi _{t}({\overrightarrow {a'}},{\overrightarrow {b'}},G')\circ \varphi _{t}({\overrightarrow {a}},{\overrightarrow {b}},G)({\overrightarrow {x}})=GG'{\overrightarrow {x}}+(G'{\overrightarrow {a}}+{\overrightarrow {a'}})+(G{\overrightarrow {b}}+{\overrightarrow {b'}})\cdot t\\=\varphi _{t}(G'{\overrightarrow {a}}+{\overrightarrow {a'}},G{\overrightarrow {b}}+{\overrightarrow {b'}},GG')({\overrightarrow {x}})\end{aligned}}}$ 对应的有：
空间平移：${\displaystyle \varphi _{t}({\overrightarrow {a}},{\overrightarrow {0}},\mathbf {I} )({\overrightarrow {x}})={\overrightarrow {x}}+{\overrightarrow {a}}}$
速度变换：${\displaystyle \varphi _{t}({\overrightarrow {0}},{\overrightarrow {b}},\mathbf {I} )({\overrightarrow {x}})={\overrightarrow {x}}+{\overrightarrow {b}}\cdot t}$
空间旋转：${\displaystyle \varphi _{t}({\overrightarrow {0}},{\overrightarrow {0}},G)({\overrightarrow {x}})=G{\overrightarrow {x}}}$
${\displaystyle \varphi _{t}({\overrightarrow {a}},{\overrightarrow {b}},G)}$为不含时伽利略群，加上时间平移${\displaystyle t\mapsto t+t_{0}}$后映射${\displaystyle ({\overrightarrow {x}},t)\mapsto (\varphi _{t},t+t_{0})=(G{\overrightarrow {x}}+{\overrightarrow {a}}+{\overrightarrow {b}}\cdot t,t+t_{0})}$构成一个完整伽利略群，其依旧满足群的性质。完整伽利略群具有10个生成元，分别为3个空间平移(x,y,z)，3个空间转动(对应3个坐标基矢），3个速度，以及一个时间平移。

伽利略群的中心扩张

这里我们只考虑伽利略群的李代数。结果能够轻易延伸到李群。L的李代数由H、P_i、C_i和L_ij张成（反对称张量），并能够受交换子的作用，其中

${\displaystyle [H,P_{i}]=0\,\!}$

${\displaystyle [P_{i},P_{j}]=0\,\!}$

${\displaystyle [L_{ij},H]=0\,\!}$

${\displaystyle [C_{i},C_{j}]=0\,\!}$

${\displaystyle [L_{ij},L_{kl}]=i[\delta _{ik}L_{jl}-\delta _{il}L_{jk}-\delta _{jk}L_{il}+\delta _{jl}L_{ik}]\,\!}$

${\displaystyle [L_{ij},P_{k}]=i[\delta _{ik}P_{j}-\delta _{jk}P_{i}]\,\!}$

${\displaystyle [L_{ij},C_{k}]=i[\delta _{ik}C_{j}-\delta _{jk}C_{i}]\,\!}$

${\displaystyle [C_{i},H]=iP_{i}\,\!}$

${\displaystyle [C_{i},P_{j}]=0\,\!.}$

H为时间平移的生成元（哈密顿算符），P_i为平移的生成元（动量算符），C_i为伽利略变换的生成元，而L_ij为旋转的生成元（角动量算符）。

现在我们可以对H'、P'_i、C'_i、L'_ij（反对称张量）、M所张成的李群进行中心扩张，使得M与一切都可交换（位于中心，“中心扩张”因此得名）：

${\displaystyle [H',P'_{i}]=0\,\!}$

${\displaystyle [P'_{i},P'_{j}]=0\,\!}$

${\displaystyle [L'_{ij},H']=0\,\!}$

${\displaystyle [C'_{i},C'_{j}]=0\,\!}$

${\displaystyle [L'_{ij},L'_{kl}]=i[\delta _{ik}L'_{jl}-\delta _{il}L'_{jk}-\delta _{jk}L'_{il}+\delta _{jl}L'_{ik}]\,\!}$

${\displaystyle [L'_{ij},P'_{k}]=i[\delta _{ik}P'_{j}-\delta _{jk}P'_{i}]\,\!}$

${\displaystyle [L'_{ij},C'_{k}]=i[\delta _{ik}C'_{j}-\delta _{jk}C'_{i}]\,\!}$

${\displaystyle [C'_{i},H']=iP'_{i}\,\!}$

${\displaystyle [C'_{i},P'_{j}]=iM\delta _{ij}\,\!}$

参见

• 洛伦兹群
• 庞加莱群