热门问题
时间线
聊天
视角
希尔伯特变换
来自维基百科,自由的百科全书
Remove ads
在数学和讯号处理中,希尔伯特变换(英语:Hilbert transform)是一个对函数 u(t) 产生定义域相同的函数 H(u)(t) 的线性算子。
希尔伯特变换在讯号处理中很重要,能够导出讯号 u(t) 的解析表示。这就意味着将实讯号 u(t) 拓展到复平面,使其满足柯西-黎曼方程。 例如,希尔伯特变换引出了傅里叶分析中给定函数的调和共轭,也就是调和分析。等价地说,它是奇异积分算子与傅里叶乘子的一个例子。
希尔伯特变换最初只对周期函数(也就是圆上的函数)有定义,在这种情况下它就是与希尔伯特核的卷积。然而更常见的情况下,对于定义在实直线 R(上半平面的边界)上的函数,希尔伯特变换是指与柯西核卷积。希尔伯特变换与帕利-维纳定理有着密切的联系,帕利-维纳定理是将上半平面内的全纯函数与实直线上的函数的傅里叶变换相联系起来的另一种结果。
希尔伯特变换是以大卫·希尔伯特来命名的,他首先引入了该算子来解决全纯函数的黎曼–希尔伯特问题的一个特殊情况。

Remove ads
定义
的希尔伯特变换可以认为是 与函数 的卷积。由于 是不可积的,定义卷积的积分不收敛。因而希尔伯特变换是使用柯西主值(这里记为)定义的。准确说来,函数(或讯号) 的希尔伯特变换是:
假设此积分作为主值存在。这就是 u 与缓增分布 p.v. 1/πt 的卷积(由于Schwartz (1950);参见Pandey (1996,Chapter 3))。另外,通过改变变量,主值积分可以显式地(Zygmund 1968,§XVI.1)写为:
若希尔伯特变换接连用在函数 u 上两次,结果就是负 u:
假设定义两次迭代的积分都收敛。特别地,逆变换是 −H。可以通过考虑 u(t) 的傅里叶变换的希尔伯特变换效应看出这一事实(参见下面的与傅里叶变换的关系)。
对上半平面的解析函数,希尔伯特变换描述了边界值的实部与虚部之间的关系。也就是说,如果 f(z) 是在 Im z > 0 平面内的解析函数,而 u(t) = Re f(t + 0·i ),假设希尔伯特变换存在,则 Im f(t + 0·i ) = H(u)(t) 取决于一个相加性常数。
Remove ads
其中
即为符号函数。
既然:
- ,
希尔伯特变换会将负频率成分偏移+90°,而正频率成分偏移−90°。
Remove ads
我们也注意到:。因此将上面方程式乘上,可得到:
从中,可以看出反(逆)希尔伯特变换
希尔伯特变换表格
- Notes
- Some authors (e.g., Bracewell) use our −H as their definition of the forward transform. A consequence is that the right column of this table would be negated.
- The Hilbert transform of the sin and cos functions can be defined in a distributional sense, if there is a concern that the integral defining them is otherwise conditionally convergent. In the periodic setting this result holds without any difficulty.
常数之希尔伯特变换为零
Remove ads
特性
若 1<p<∞,则 Lp(R)之希尔伯特变换为一有界算子,表示存在一常数Cp使得
对所有 u∈Lp(R)。这个定理由Riesz (1928,VII)所推得;请一并参见Titchmarsh (1948,Theorem 101)。 最佳常数Cp可由下列算式得到:
这个结果由(Pichorides 1972)所推得;请一并参见Grafakos (2004,Remark 4.1.8)。上述最佳常数计算方式应用在周期性希尔伯特变换一样成立。
希尔伯特变换的边界指的是 Lp(R) 对称级数运算子对于在 Lp(R) 之中 f 的收敛
请参见(Duoandikoetxea 2000,第59页)。
Remove ads
希尔伯特变换为一反自伴算子,连结 Lp(R) 与其对偶空间 Lq(R),其中 p 和 q 为 赫尔德共轭且 1 < p,q < ∞. 以符号表示
对 u ∈ Lp(R) 且 v ∈ Lq(R) (Titchmarsh 1948,Theorem 102).
Remove ads
希尔伯特变换为一反-对合 (Titchmarsh 1948,第120页),意即
假定每一变换皆完整定义过。由于 H 保存了 Lp(R)空间,这特别代表希尔伯特变换在 Lp(R) 上是可逆的,且
Remove ads
正式上,一个式子其希尔伯特变换的微分即为其微分的希尔伯特变换,意即这两者是可以交换的线性算子
此一特性亦可迭代
给定 u 以及其前k次微分皆属于Lp(R) (Pandey 1996,§3.3)空间,此项论述为严格成立。在频域上可以轻易验证这件事情,由于微分在频域上即为与 ω 之乘积。
希尔伯特变换可表示为与一缓增分布之旋积 (Duistermaat & Kolk 2010,第211页)
因此可如此表示
然而,事前此特性可能只有对紧支撑之分布 u定义。由于紧支撑函数在 Lp 上是稠密的,因此此项特性可能严格成立。另一角度来看,也可使用 h(t) 其微分之特性来证明
在大部分的用途,希尔伯特变换可被视为是一旋积。举例而言,旋积与希尔伯特变换具备下列可交换的特性
若 u 和 v 为紧支撑分布,则此项论述严格成立,在这个状况下
Remove ads
希尔伯特变换在空间 L2(R) 上有下列特性
- 可与算子 Taƒ(x) = ƒ(x + a) 交换,对所有实数 a
- 可与算子 Mλƒ(x) = ƒ(λx) 交换,对所有 λ > 0
- 可与镜射 Rƒ(x) = ƒ(−x) 反交换
实际上,有更大一部分的算子可与希尔伯特变换交换。群组 SL(2,R) 由幺正算符 Ug 可在空间 L2(R) 上由以下式子表示
Remove ads
希尔伯特变换例子
注意:有些作者,例如Bracewell,将我们的当作其正变换的定义。这样的结果就是下表右行要乘上一个负号。
离散希尔伯特变换




对于一离散函数 u[n],以及其 离散傅里叶变换 函数 U(ω),可推得其希尔伯特变换为:
其中
此外,根据卷积定律,另一个相等的方程式为:
其中
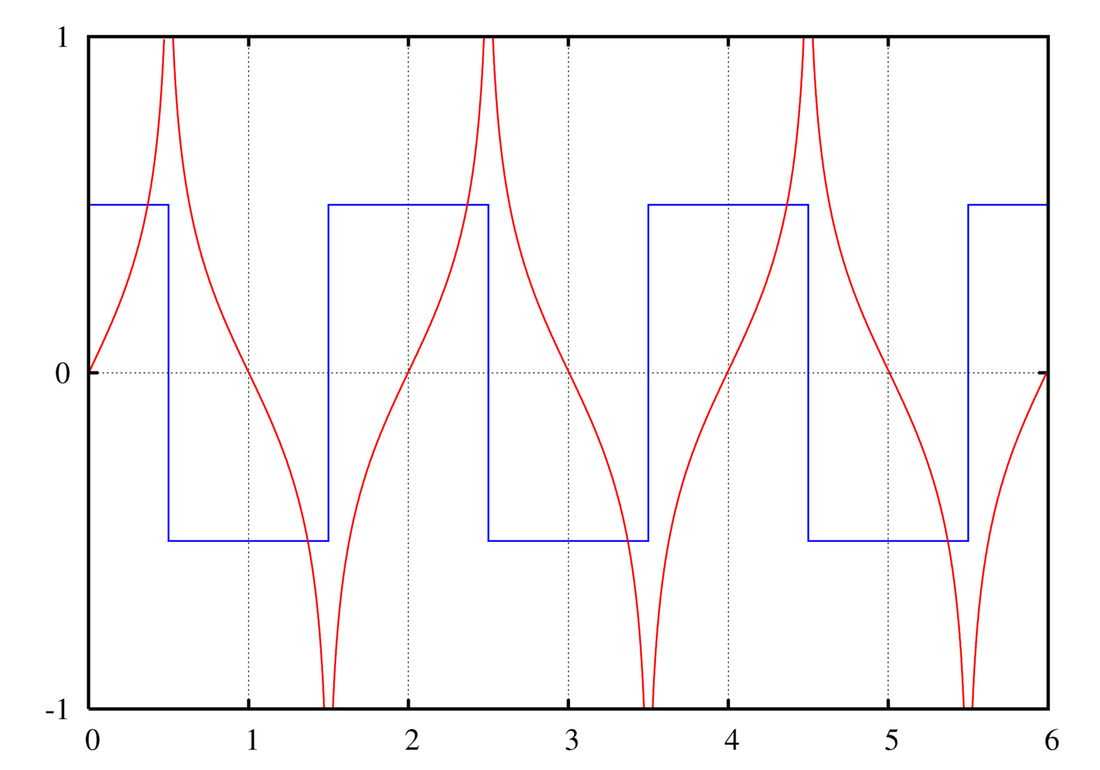
当卷积经由数值运算后,一FIR 近似将取代h[n],如 图 1所示,可以见到频率响应在通带之两端(0与奈奎斯特频率)的陡降,形成一带通滤波器。其中高频部分可借由一FIR滤波器回复,如 图 2所示。然而实际上,一个经过适当采样的 u[n] 串行在高频部分已经不具有可用的分量。当冲激响应持续越久,低频部分也可以被回复。
用FIR近似h[n]的时候,交叠储存法是一个对于很长的u[n] 串行做卷积运算的有效方法。有时候阵列FFT{h[n]}会被σH(ω)相对应之采样串行所取代。如此将会有与周期叠加函数做卷积之效果:
图 3比较了hN[n]之半周期与一相同长度分量之h[n]。两者之间之差异与两者之长度皆不短于区段长度(N)之现象为失真的来源,且失真可经由增加区段长度与交叠参数来有效减少。
MATLAB中有一函数 hilbert(u,N),此函数会回传一复数串行,其中虚部串行为 u[n]之离散希尔伯特变换近似,实部串行为原本输入之串行,所以这样的复数输出等于是 u[n]的分析讯号。与前述类似, hilbert(u, N) 只使用来自 sgn(ω)分布的采样,因此是与 hN[n] 的卷积。如前段所述,失真可借由选择比实际之u[n]串行更大的N与舍弃适当数量的输出采样来有效减少。图 4为这种失真的一个例子。
相关条目
参考文献
- Bargmann, V., Irreducible unitary representations of the Lorentz group, Ann. of Math., 1947, 48 (3): 568–640, JSTOR 1969129, doi:10.2307/1969129
- Bedrosian, E., A Product Theorem for Hilbert Transforms (PDF), Rand Corporation Memorandum, December 1962, (RM-3439-PR) [2016-08-05], (原始内容存档 (PDF)于2021-02-25)
- Benedetto, John J. Harmonic analysis and applications. Boca Raton, FL: CRC Press. 1996. ISBN 0849378796.
- Bitsadze, A.V., Boundary value problems of analytic function theory, 数学百科全书, EMS Press, 2001 (英语).
- Bracewell, R., The Fourier Transform and Its Applications 3rd, McGraw–Hill, 2000, ISBN 0-07-116043-4.
- Calderón, A.P.; Zygmund, A., On the existence of certain singular integrals, Acta Mathematica, 1952, 88 (1): 85–139, doi:10.1007/BF02392130.
- Carlson, Crilly, and Rutledge, Communication Systems 4th, 2002, ISBN 0-07-011127-8.
- Duoandikoetxea, J., Fourier Analysis, American Mathematical Society, 2000, ISBN 0-8218-2172-5.
- Duistermaat, J.J.; Kolk, J.A.C. Kolk, Distributions, Birkhäuser, 2010, ISBN 978-0-8176-4672-1, doi:10.1007/978-0-8176-4675-2.
- Duren, P., Theory of -Spaces, New York: Academic Press, 1970.
- Fefferman, C., Characterizations of bounded mean oscillation, Bull. Amer. Math. Soc., 1971, 77 (4): 587–588, MR 0280994, doi:10.1090/S0002-9904-1971-12763-5.
- Fefferman, C.; Stein, E.M., Hp spaces of several variables, Acta Math., 1972, 129: 137–193, MR 0447953, doi:10.1007/BF02392215.
- Gel'fand, I.M.; Shilov, G.E., Generalized Functions, Vol. 2, Academic Press, 1967.
- Grafakos, Loukas, An Elementary Proof of the Square Summability of the Discrete Hilbert Transform, American Mathematical Monthly (Mathematical Association of America), 1994, 101 (5): 456–458, JSTOR 2974910, doi:10.2307/2974910.
- Grafakos, Loukas, Classical and Modern Fourier Analysis, Pearson Education, Inc.: 253–257, 2004, ISBN 0-13-035399-X.
- Hardy, G. H.; Littlewood, J. E.; Polya, G., Inequalities, Cambridge: Cambridge University Press, 1952, ISBN 0-521-35880-9.
- Hilbert, David, Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen, Chelsea Pub. Co., 1953
- Kak, Subhash, The discrete Hilbert transform, Proc. IEEE, 1970, 58: 585–586 .
- Kak, Subhash, Number theoretic Hilbert transform, Circuits Systems Signal Processing, 2014, 33: 2539–2548 .
- Khvedelidze, B.V., Hilbert transform, 数学百科全书, EMS Press, 2001 (英语).
- King, Frederick W., Hilbert Transforms 2, Cambridge: Cambridge University Press: 453, 2009, ISBN 978-0-521-51720-1.
- Kress, Rainer, Linear Integral Equations, New York: Springer-Verlag: 91, 1989, ISBN 3-540-50616-0.
- Lang, Serge, SL(2,R), Graduate Texts in Mathematics 105, Springer-Verlag, 1985, ISBN 0-387-96198-4
- Pandey, J.N., The Hilbert transform of Schwartz distributions and applications, Wiley-Interscience, 1996, ISBN 0-471-03373-1
- Pichorides, S., On the best value of the constants in the theorems of Riesz, Zygmund, and Kolmogorov, Studia Mathematica, 1972, 44: 165–179
- Riesz, Marcel, Sur les fonctions conjuguées, Mathematische Zeitschrift, 1928, 27 (1): 218–244, doi:10.1007/BF01171098
- Rosenblum, Marvin; Rovnyak, James, Hardy classes and operator theory, Dover, 1997, ISBN 0-486-69536-0
- Schwartz, Laurent, Théorie des distributions, Paris: Hermann, 1950.
- Schreier, P.; Scharf, L., Statistical signal processing of complex-valued data: the theory of improper and noncircular signals, Cambridge University Press, 2010
- Stein, Elias, Singular integrals and differentiability properties of functions, Princeton University Press, 1970, ISBN 0-691-08079-8.
- Stein, Elias; Weiss, Guido, Introduction to Fourier Analysis on Euclidean Spaces, Princeton University Press, 1971, ISBN 0-691-08078-X.
- Sugiura, Mitsuo, Unitary Representations and Harmonic Analysis: An Introduction, North-Holland Mathematical Library 44 2nd, Elsevier, 1990, ISBN 0444885935
- Titchmarsh, E, Reciprocal formulae involving series and integrals, Mathematische Zeitschrift, 1926, 25 (1): 321–347, doi:10.1007/BF01283842.
- Titchmarsh, E, Introduction to the theory of Fourier integrals 2nd, Oxford University: Clarendon Press, 19481986, ISBN 978-0-8284-0324-5.
- Zygmund, Antoni, Trigonometric series 2nd, Cambridge University Press, 19681988, ISBN 978-0-521-35885-9.
外部链接
- The Discrete Hilbert Transform; A Brief Tutorial_w236 (页面存档备份,存于互联网档案馆)
- Derivation of the boundedness of the Hilbert transform (页面存档备份,存于互联网档案馆)
- Mathworld Hilbert transform (页面存档备份,存于互联网档案馆) — Contains a table of transforms
- Analytic Signals and Hilbert Transform Filters
- 埃里克·韦斯坦因. Titchmarsh theorem. MathWorld.
- Mathias Johansson, "The Hilbert transform" a student level summary to Hilbert transformation. [失效链接] (via www.archive.org)
- GS256 Lecture 3: Hilbert Transformation, an entry level introduction to Hilbert transformation. [失效链接] (via www.archive.org)
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads


















 ...
...


















![{\displaystyle \chi _{[a,b]}(t)\,}](http://wikimedia.org/api/rest_v1/media/math/render/svg/8d0b54b72a85ccee7e0ebaed888aede9c83b775c)
















![{\displaystyle H(u)[n]=\scriptstyle {DTFT}^{-1}\displaystyle \{U(\omega )\cdot \sigma _{H}(\omega )\}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/98ccbef3d06ddf3d6d2b5677a723b699fde67cc4)

![{\displaystyle H(u)[n]=u[n]*h[n]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/142ff40246b6744504437a7a68edd7b30b0f088c)
![{\displaystyle h[n]\ {\stackrel {\mathrm {def} }{=}}\ \scriptstyle {DTFT}^{-1}{\big \{}\displaystyle \sigma _{H}(\omega ){\big \}}={\begin{cases}0,&{\mbox{for }}n{\mbox{ even}}\\{\frac {2}{\pi n}}&{\mbox{for }}n{\mbox{ odd}}\end{cases}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/5957aca8a4ab2c49a6cc33db4aa293966c56a02c)
![{\displaystyle h_{N}[n]\ {\stackrel {\text{def}}{=}}\ \sum _{m=-\infty }^{\infty }h[n-mN]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/cc384c379a22eb9e01cc550353c2fe9070de459d)
