ΛCDM模型

ΛCDM模型（英語：ΛCDM Model）是所謂Λ-冷暗物質（Lambda Cold Dark Matter）模型的簡稱。它在大爆炸宇宙學中經常被稱作索引模型，這是因為它嘗試解釋了對宇宙微波背景輻射、宇宙大尺度結構以及宇宙加速膨脹的超新星觀測。它是當前能夠對這些現象提供融洽合理解釋的最簡單模型。

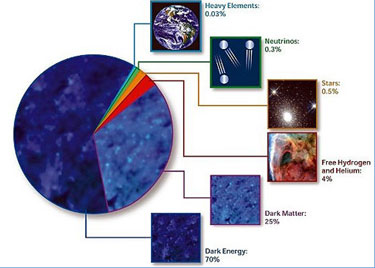
• Λ意為宇宙學常數，是解釋當前宇宙觀測到的加速膨脹的暗能量項。宇宙學常數經常用${\displaystyle \Omega _{\Lambda }\,}$表示，含義是當前宇宙中暗能量相對於一個平直時空的宇宙的能量所占的比例。最近對${\displaystyle \Omega _{\Lambda }\,}$的觀測結果包括暗能量巡天測得的66.9%^[1]，以及2018年普朗克衛星通過微波背景輻射測得比例約為68.3%。^[2]
• 冷暗物質是一種暗物質模型，即它認為在宇宙早期輻射與物質的能量分布相當時暗物質的速度是非相對論性的（遠小於光速），因此暗物質是冷的；同時它們是非重子構成的；不會發生碰撞（指暗物質的粒子不會與其他物質粒子發生重力以外的基本交互作用）或能量損耗（指暗物質不會以光子的形式輻射能量）的。冷暗物質占了當前宇宙能量密度的26.5%。^[3]剩餘的4.9%的包括宇宙中所有的由重子（以及光子等規範玻色子）構成的物質：行星、恆星以及氣體星雲等。^[4]
• 模型假設了具有接近尺度不變的能量譜的太初微擾，以及一個空間曲率為零的宇宙。它同時假設了宇宙沒有可觀測的拓撲，從而宇宙實際要比可觀測的粒子視界要大很多。這些都是宇宙暴脹理論的預言。
• 模型採用了傅里德曼-勒梅特-羅伯遜-沃克度規、傅里德曼方程式和宇宙的狀態方程式來描述從暴脹時期之後至今以及未來的宇宙。

一張表示宇宙間不同物質能量成分的餅圖，大約有96%的能量來自奇異的暗物質和暗能量。

ΛCDM模型，加速擴張的宇宙。

在宇宙學中，這些是能夠構建一個自洽的物理宇宙模型的最簡單的假設。而ΛCDM模型終歸只是一個模型，宇宙學家們預計在對相關的基礎物理了解更多之後，這些簡單的假設都有可能被證明並不完全準確。具體而言，暴脹理論預言宇宙的空間曲率在10^-5到10^-4的量級。另外也很難相信暗物質的溫度是絕對零度。ΛCDM模型也並沒有在基礎物理層面上解釋暗物質、暗能量以及具有接近尺度不變的能量譜的太初微擾的起源：從這個意義上說，它僅僅是一個有用的參數化形式。

參數

模型含有六個基本參數。

• 哈伯；常數——決定宇宙的膨脹速率，以及宇宙閉合所需的臨界密度${\displaystyle \rho _{0}\,}$。
• 重子的密度、暗物質的密度和暗能量的密度，它們都歸一到臨界密度，即如${\displaystyle \Omega _{b}=\rho _{b}/\rho _{0}\,}$。由於模型假設空間是平直的，三者的密度之和等於臨界密度，從而暗能量的密度並不是一個獨立參數。
• 光深度——決定宇宙再電離的紅移。
• 密度漲落的資訊由太初微擾的漲落振幅（源自宇宙暴脹）和能譜指數共同決定，其中能譜指數${\displaystyle n_{s}\,}$表徵漲落如何隨尺度變化（${\displaystyle n_{s}=1\,}$表示尺度不變的能譜）。

模型中包含的誤差分析顯示，實際的真實值有68%的置信機率落到測量結果的上下限之間。誤差並不是非高斯分布的，它們是通過對威爾金森微波各向異性探測器的數據以蒙特卡羅馬爾可夫鏈方法進行誤差分析得出的，其中也使用了史隆數位巡天和Ia型超新星的觀測數據。

參數	數值	描述
基本參數
Ωb	${\displaystyle 0.0486_{-0.0010}^{+0.0010}}$	重子密度
Ωc	${\displaystyle 0.2589_{-0.0057}^{+0.0057}}$	暗物質密度
t0	${\displaystyle 13.799_{-0.021}^{+0.021}\times 10^{9}}$y	宇宙的年齡
ns	${\displaystyle 0.9667_{-0.0040}^{+0.0040}}$	尺度能譜指數
${\displaystyle \Delta _{R}^{2}}$	${\displaystyle 2.441_{-0.092}^{+0.088}\times 10^{-9}}$	尺度漲落振幅， k0 = 0.002 Mpc-1
τ	${\displaystyle 0.066_{-0.012}^{+0.012}}$	宇宙再電離所需的光深度
固定參數
Ωtot	${\displaystyle 1}$	空間曲率
w	${\displaystyle -1}$	狀態方程式
r	${\displaystyle 0}$	張量純量比
d ns / d ln k	${\displaystyle 0}$	能譜指數的變化
Σmν	${\displaystyle 0.06}$ eV/c2	微中子質量總和
Neff	${\displaystyle 3.046}$	有效的自由相對論度數
導出參數
H0	${\displaystyle 67.74_{-0.46}^{+0.46}}$ km s-1 Mpc-1	哈伯；常數
Ωm	${\displaystyle 0.3089_{-0.0062}^{+0.0062}}$	總物質密度（重子+暗物質）
ΩΛ	${\displaystyle 0.6911_{-0.0062}^{+0.0062}}$	暗能量密度
ρcrit	${\displaystyle 8.62_{-0.12}^{+0.12}\times 10^{-27}}$ kg/m3	臨界密度
σ8	${\displaystyle 0.8159_{-0.0086}^{+0.0086}}$	星系漲落指數 在平均8h-1 Mpc半徑的球形上
zre	${\displaystyle 8.5_{-1.1}^{+1.0}}$	再電離紅移

ΛCDM模型的優勢

在所有宇宙學模型中，ΛCDM模型取得了最顯著的成功；它以卓越的精確度描述了涵蓋幾乎所有領域的天文觀測結果。^[5]​其主要成功之處包括：

• 精確擬合普朗克衛星和阿塔卡馬宇宙學望遠鏡觀測到的宇宙微波背景輻射角功率譜。^[2][6]
• 準確描述由於最後散射面波動引起的CMB輻射的線性E模偏振。^[7]
• 準確預測由原初重力波引起的CMB輻射的B模式偏振。^[8]
• 觀測到來自128億光年外星系的H₂O發射譜，與由比我們當前觀測到的3K CMB更高能量（16-20K）的宇宙背景輻射激發的分子相一致。^[9]
• 準確預測了由大爆炸核合成產生的氘的原初豐度。^[10]

除了成功解釋2000年前的多項觀測外，該模型還做出了多項成功預測：

• 成功預測了重子聲學振盪特徵，並於2005年由SDSS和2dFGRS研究組發現；^[11]
• 成功預測了2000年首次觀測到的弱重力透鏡統計特性；
• 成功預測了2002年由DASI發現的CMB偏振特性。

在2015年普朗克數據發布中，溫度（TT）功率譜中觀測到七個峰值，溫度-偏振（TE）交叉譜中六個峰值，以及偏振（EE）譜中五個峰值。​僅通過TT譜就能很好地約束六個自由參數，然後TE和EE譜可以在沒有進一步調整的情況下，由ΛCDM模型以百分之幾的精度進行理論預測。

擴展模型

由最簡單的ΛCDM模型可以進一步擴展為其他模型，例如可以用第五元素替代宇宙常數項，在這種情況下暗能量的狀態方程式可以為-1以外的其他值。宇宙暴脹預言了時空度規張量的漲落（即重力波），它們的振幅可由張量純量比（tensor-to-scalar ratio）參數化，而後者由暴脹的能量尺度決定。其他對模型的修正包括允許空間曲率的存在或隨時間變化的能譜指數，這些在一般觀點看來都是和暴脹理論相違背的。

允許引入這些參數通常都會增加上述基本參數的測量誤差，並在某種程度上使測量值產生偏移。

參數	數值	描述
${\displaystyle \Omega _{tot}}$	${\displaystyle 1.0023_{-0.0054}^{+0.0056}}$	空間曲率
${\displaystyle w}$	${\displaystyle -0.980_{-0.053}^{+0.053}}$	狀態方程式
${\displaystyle r}$	${\displaystyle <0.11}$, k0 = 0.002 Mpc-1 (2σ)	張量純量比
${\displaystyle d\ n_{s}/d\ \ln k}$	${\displaystyle -0.022_{-0.020}^{+0.020}}$, k0 = 0.002 Mpc-1	能譜指數的變化
${\displaystyle \Sigma m_{\nu }}$	${\displaystyle <0.58}$ eV/c2 (2σ)	微中子質量總和
${\displaystyle \Omega _{v}h^{2}}$	${\displaystyle <0.0062}$	物理微中子密度參數

這些參數與一個具有參數${\displaystyle \omega =-1\,}$的宇宙的狀態方程式、以及一個空間曲率為零的情形相洽。